순열(Permutation) / 조합 (Combination)
순열 조합 문제 예시
카드 뽑기
[A, B, C, D, E]로 이뤄진 5장의 카드가 있습니다. 이 5장의 카드 중 3장을 선택하여 나열하려고 합니다. 이때, 다음의 조건을 각각 만족하는 경우를 찾아야 합니다.
조건 1. 순서를 생각하며 3장을 선택합니다.
조건 2. 순서를 생각하지 않고 선택합니다.
조건 1을 만족하는 모든 경우의 수
1번 조건에서 모든 경우의 수를 구할 때에는 모든 카드를 1장씩 나열하면서 나열된 카드가 3장에 도달하면 카드의 나열을 중지합니다.
1번의 조건을 만족하려면, 다음과 같은 방법으로 경우의 수를 구합니다.
- 첫번째 나열하는 카드를 선택하는 방법에는 다섯 가지가 있습니다.
(A,B,C,D,E 중 하나를 뽑는다.) - 첫번째 카드를 나열하고 난 다음, 두번째 카드를 선택하는 방법에는 네 가지가 있습니다.
(예를 들어 처음에 A를 뽑았다면 나머지 B,C,D,E 중 하나를 뽑는다.) - 두번째 카드를 나열하고 난 다음, 세번째 카드를 선택하는 방법에는 세 가지가 있습니다.
(처음에 A를 뽑고, 그 다음 C를 뽑았다면, 나머지 B,D,E 중 하나를 뽑고 종료)
따라서 5 X 4 X 3 = 60 가지의 방법이 있습니다.
이렇게 n 개 중에서 일부만을 선택하여 나열하는 것을 순열이라고 합니다. 순열은 순서를 지키며 나열해야 합니다. 예를 들어 카드를 3장 뽑을 때, [A, B, D]와 [A, D, B] 두 경우 모두 A, B, 그리고 D라는 같은 카드를 3장 선택했지만, 나열하는 순서가 다르므로 서로 다른 경우로 파악해야 합니다.
순열은 일반화 과정을 거쳐, Permutation의 약자 P로 표현합니다.
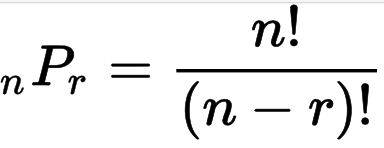
조건 2를 만족하는 모든 경우의 수
2번 조건에서 모든 경우의 수를 구할 때는 3장을 하나의 그룹으로 선택해야 합니다. 2번의 조건을 만족하려면, 다음과 같은 방법으로 경우의 수를 구합니다.
- 순열로 구할 수 있는 경우를 찾습니다.
- 순열로 구할 수 있는 경우에서 중복된 경우의 수를 나눕니다.
먼저, 조합은 순열과 달리 순서를 고려하지 않습니다. 만약 순열처럼 순서를 생각하여 경우의 수를 센다면, 조합으로써 올바르지 않을 겁니다. 예를 들어 순열에서는 [A, B, C], [A, C, B], [B, A, C], [B, C, A], [C, A, B], [C, B, A]의 여섯 가지는 모두 다른 경우로 취급하지만, 조합에서는 이 여섯 가지를 하나의 경우로 취급합니다. 다시 말해 순열에서처럼 순서를 생각하여 선택하면, 중복된 경우가 6배 발생합니다.
여기서 나온 여섯 가지 경우의 수는 3장의 카드를 순서를 생각하여 나열한 모든 경우의 수입니다. 3장의 카드를 순열 공식에 적용한 결과가 3! / (3-3)! = (3 X 2 X 1) / 1 = 6 입니다. 순서를 생각하느라 중복된 부분이 발생한 순열의 모든 가짓수를, 중복된 6가지로 나누어 주면 조합의 모든 경우의 수를 얻을 수 있습니다.
따라서 (5 X 4 X 3 X 2 X 1) / ((3 X 2 X 1) X (2 X 1)) = 10 입니다.
조합은 일반화 과정을 거쳐, Combination의 약자 C로 표현합니다.
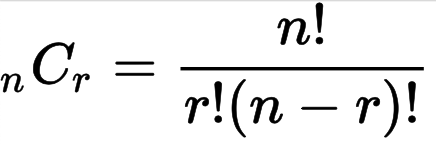
- 5장에서 3장을 무작위로 선택하는 조합에서 모든 경우의 수 = 5C3 = 5! / (3! * 2!) = 10
- 일반식: nCr = n! / (r! * (n - r)!)
최대공약수(GCD) / 최소공배수(LCM)
용어정리
- 약수: 어떤 수를 나누어떨어지게 하는 수
- 배수: 어떤 수의 1, 2, 3, ...n 배하여 얻는 수
- 공약수: 둘 이상의 수의 공통인 약수
- 공배수: 둘 이상의 수의 공통인 배수
- 최대 공약수(GCD. Greatest Common Divisor): 둘 이상의 공약수 중에서 최대인 수
- 최소 공배수(LCM. Least Common Multiple): 둘 이상의 공배수 중에서 최소인 수
GCD / LCM 공식
최대공약수와 최소공배수를 코드로 구현하는 방법은 여러가지가 있겠지만, 유클리드 호제법을 이용해서 코드를 공식화 시켜서 사용할 수 있다.
function CGD (a, b) {
if(a % b === 0) return b
return GCD(b, a % b)
}
function LCM (a, b) {
return a * b / GCD(a, b)
}
// 위 코드를 삼항연산자를 사용해서 간단히 하면 아래와 같다.
const GCD = (a, b) => a % b === 0 ? b : GCD(b, a % b);
const LCM = (a, b) => a * b / GCD(a, b);멱집합(PowerSet)
집합 {1, 2, 3}의 모든 부분집합은 {}, {1}, {2}, {3}, {1, 2}, {1, 3}, {2, 3}, {1, 2, 3} 으로 나열할 수 있고, 이 부분집합의 총 개수는 8개입니다. 그리고 이 모든 부분집합을 통틀어 멱집합이라고 합니다. 이렇게 어떤 집합이 있을 때, 이 집합의 모든 부분집합을 멱집합 이라고 합니다. 모든 부분집합을 나열하는 방법은 다음과 같이 몇 단계로 구분할 수 있습니다. 부분집합을 나열하는 방법에서 가장 앞 원소(혹은 임의의 집합 원소)가 있는지, 없는지에 따라 단계를 나누는 기준을 결정합니다.
- Step A: 1을 제외한 {2, 3}의 부분집합을 나열합니다.
- Step B: 2를 제외한 {3}의 부분집합을 나열합니다.
- Step C: 3을 제외한 {}의 부분집합을 나열합니다. → {}
- Step C: {}의 모든 부분집합에 {3}을 추가한 집합들을 나열합니다. → {3}
- Step B: {3}의 모든 부분집합에 {2}를 추가한 집합들을 나열합니다.
- Step C: {3}의 모든 부분집합에 {2}를 추가한 집합들을 나열하려면, {}의 모든 부분집합에 {2}를 추가한 집합들을 나열한 다음 {}의 모든 부분집합에 {2, 3}을 추가한 집합들을 나열합니다. → {2}, {2, 3}
- Step B: 2를 제외한 {3}의 부분집합을 나열합니다.
- Step A: {2, 3}의 모든 부분집합에 {1}을 추가한 집합들을 나열합니다.
- Step B: {2, 3}의 모든 부분집합에 {1}을 추가한 집합들을 나열하려면, {3}의 모든 부분집합에 {1}을 추가한 집합들을 나열한 다음 {3}의 모든 부분집합에 {1, 2}를 추가한 집합들을 나열합니다.
- Step C: {3}의 모든 부분집합에 {1}을 추가한 집합을 나열하려면, {}의 모든 부분집합에 {1}을 추가한 집합들을 나열한 다음 {}의 모든 부분집합에 {1, 3}을 추가한 집합들을 나열합니다. → {1}, {1, 3}
- Step C: {3}의 모든 부분집합에 {1, 2}를 추가한 집합을 나열하려면, {}의 모든 부분집합에 {1, 2}를 추가한 집합들을 나열한 다음 {}의 모든 부분집합에 {1, 2, 3}을 추가한 집합들을 나열합니다. → {1, 2}, {1, 2, 3}
- Step B: {2, 3}의 모든 부분집합에 {1}을 추가한 집합들을 나열하려면, {3}의 모든 부분집합에 {1}을 추가한 집합들을 나열한 다음 {3}의 모든 부분집합에 {1, 2}를 추가한 집합들을 나열합니다.
원소가 있는지, 없는지 2가지 경우를 고려하기 때문에 집합의 요소가 n 개일 때 모든 부분집합의 개수는 2n개 입니다. 예를 들어 집합의 원소가 4개라면 모든 부분집합의 개수는 24, 집합의 원소가 5개라면 25가 됩니다.
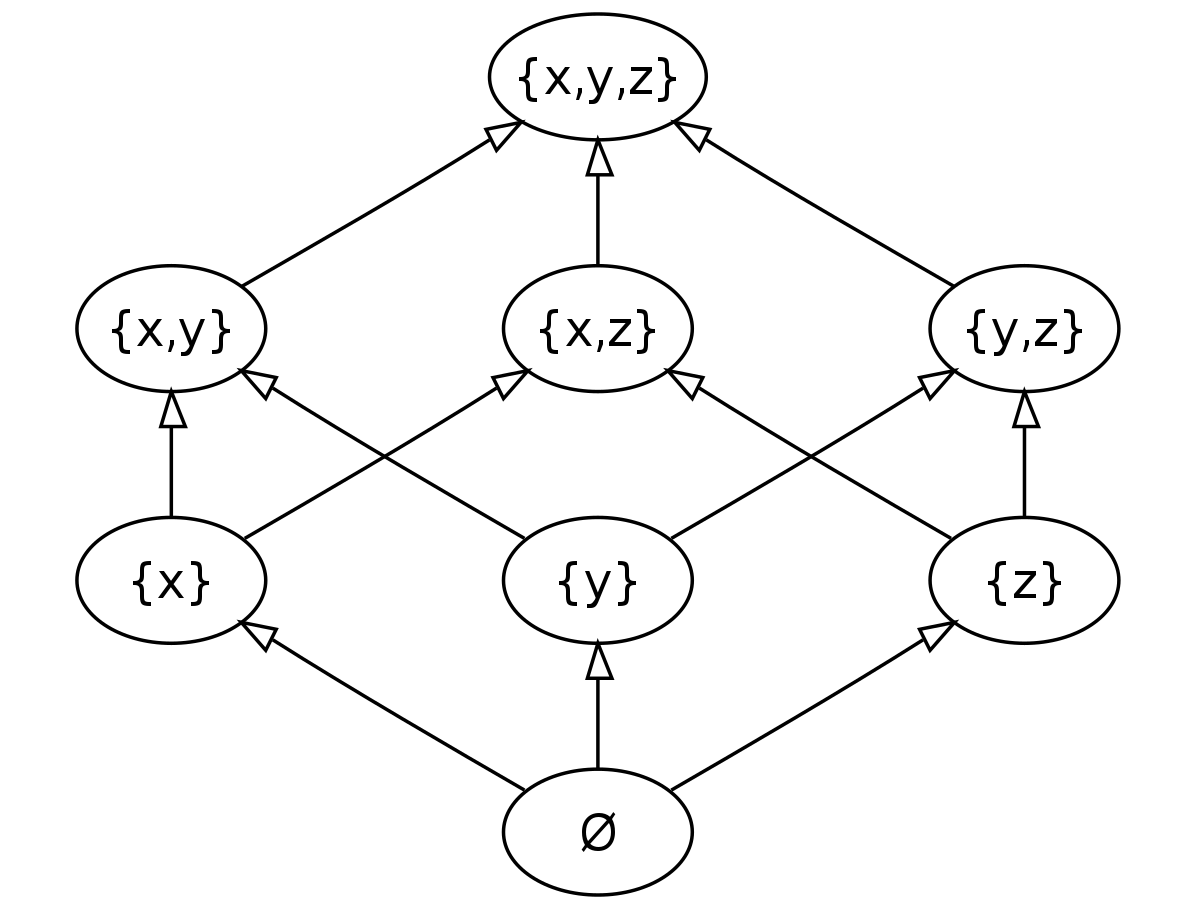
멱집합을 구하는 방법에서 각 단계를 유심히 살펴보면, 순환 구조를 띠는 것을 확인할 수 있습니다. 여기서 순환구조는 임의의 원소를 제외하면서 집합을 작은 단위로 줄여나가는 방법입니다. 따라서, 문제를 작은 단위로 줄여나가는 재귀를 응용할 수 있습니다. 예를 들어 PowerSet 이라는 멱집합의 개수를 리턴하는 함수를 작성한다면, PowerSet 함수에서 자기 자신을 호출하며 문제를 더 작은 문제로 문제의 크기를 줄여 해결할 수 있습니다. 문제가 가장 작은 단위로 줄어들고, 함수가 리턴될 때 카운트를 올리는 방식으로 멱집합의 개수를 구할 수 있습니다.
