문제 풀이

배낭 문제 알고리즘으로 풀이할 수 있는 문제다.

앱이 차지하는 메모리 용량이 $A_{i}$ 소요되는 비용이 $C_{i}$라고 쳤을 때 확보해야하는 메모리 용량 M 이상을 확보 했을 때 최소 비용을 구하는 문제다.

그러므로 배낭 문제에 대응 해보았을 때 소요되는 비용이 배낭의 사이즈고, 해당 배낭 사이즈로 가져갈 수 있는 가치의 목록들이 각각의 앱의 메모리 용량이라고 생각하면 된다.

즉 dp배열과 점화식은 다음과 같이 정의 할 수 있다.
d[i][j] - i는 현재 확인하고 있는 앱의 인덱스, 앱을 종료하거나, 종료하지 않거나 둘 중 하나다. j는 소요될 수 있는 남은 비용이다.

그러면 $d[i][j] = Max(d[i-1][j-C_{i}] + A_{i}, d[i-1][j])$ 라는 식이 나온다.

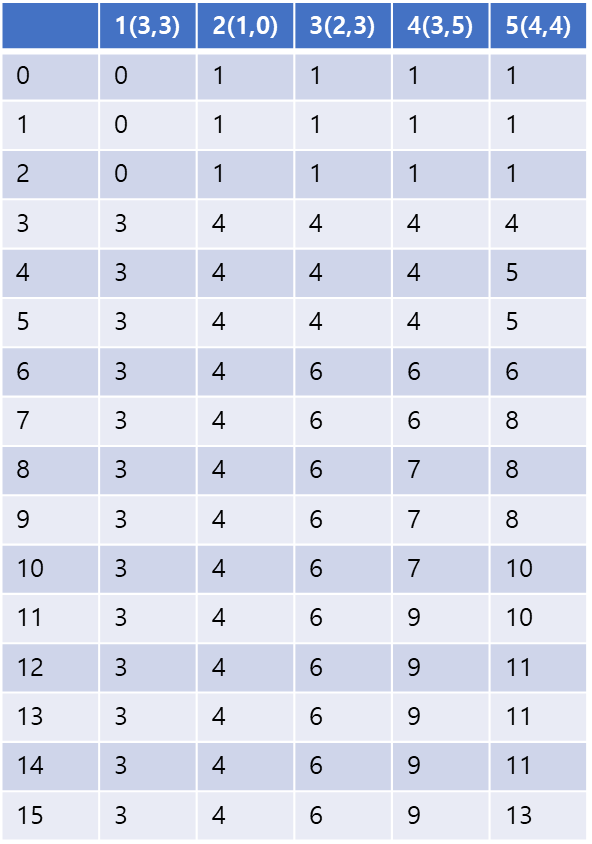
다음과 같은 예제에 dp배열 표를 그려보면 아래와 같다.

5 6
3 1 2 3 4
3 0 3 5 4

최소한 6의 메모리를 확보해야할 때 비용의 최소값은 표의 결과 값에 따라 6이 된다.

문제 링크

boj/7579

소스코드

PS/2096 .java

import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.*;

class Main {

  static int[][] arr = new int[101][2];
  static int[][] d = new int[101][10001];
  static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));

  public static void main(String[] args) throws Exception {
    StringTokenizer st = new StringTokenizer(br.readLine());
    int n = Integer.parseInt(st.nextToken());
    int m = Integer.parseInt(st.nextToken());
    st = new StringTokenizer(br.readLine());
    int sum = 0;
    int ans = 10000001;
    for (int i = 1; i <= n; i++) {
      arr[i][0] = Integer.parseInt(st.nextToken());

    }
    st = new StringTokenizer(br.readLine());
    for (int i = 1; i <= n; i++) {
      arr[i][1] = Integer.parseInt(st.nextToken());
      sum += arr[i][1];
    }
    for (int i = 1; i <= n; i++) {
      for (int j = 0; j <= sum; j++) {
        if (j - arr[i][1] >= 0) {
          d[i][j] = Math.max(d[i - 1][j - arr[i][1]] + arr[i][0], d[i - 1][j]);
        } else {
          d[i][j] = d[i - 1][j];
        }
        if (d[i][j] >= m) {
          ans = Math.min(ans, j);
        }
      }
    }
    System.out.println(ans);
  }
}