대칭 암호에서 key를 상대방과 공유하는 방법 (Key exchange)
-
RSA
key encaptualation
한쪽에서 키 생성해서 전달해주는 방법(자신의 public key 생성해서 공유) -
Diffie-Hellman(DH)
양쪽에서 key를 생성 및 공유
양쪽에서 자신의 private key와 상대의 public key로 동일한 키를 각각 생성해내 사용
Diffie-Hellman Key Exchange
목적: 대칭 암호를 사용해 메시지를 보낼 때, 두 사용자가 안전하게 key를 교환하는 것.
이것의 효율성은 discrete logarithms 계산의 어려움과 상관있다.
DH problem은 discrete log 문제보다 조금 더 엄격하다.
DH problem: {α, q, Ya, Yb}가 주어졌을 때, k(k = α^Xa,Xb mod q)를 알아내는 문제
꼭 Xa, Xb를 알아낼 필요가 없고, x와 key만 알아내면 된다.
공격자는 {α, q, Ya, Yb}는 이미 알고있다. 하지만, Ya로부터 Xa를 알아내는 건 discrete log 문제로 쉽지 않다.
즉, DH 문제는 discrete log가 어렵다는 가정에 기반한다.
RSA와 Diffie-Hellman 차이 (Forward secrecy)
| RSA | Diffie-Hellman |
|---|---|
| 한 번 해킹 당해서 {C1, d, K1}이 유출되면 지금껏 나눈 모든 대화 내용이 유출됨 => forward securecy * 매 대화마다 {e, d} 쌍을 생성하는 방법이 있지만, 오래 걸린다. | 한 번 K1를 만들 때 사용된 Xa는 유지할 필요가 없다. 매 session마다 private key를 새로 만들어서 사용하면 중간에 해킹을 당해도, 그 전의 session에서의 내용이 유출되지 않는다. |
Man in the Middle (MitM) Attack (중간자 공격)
ex) Alice가 Bob에게 Alice's public key(Ya)를 보내려고한다.
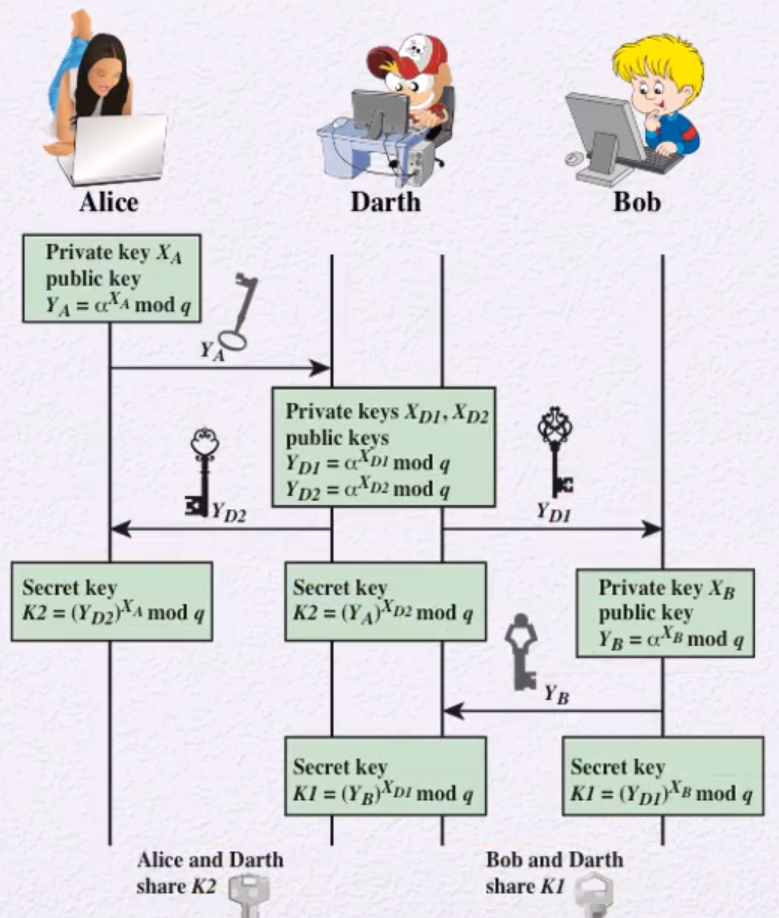
- 이때, 중간자(공격자)가 Ya를 가로채고, Bob에게 자신이 만든 가짜 Ya를 전달한다.
- Alice에게도 마찬가지로 Yb를 가로챈 후, 가짜를 전달한다.
- 이렇게 공격자는 몰래 key를 공유할 수 있다.
문제점: Authentication을 하지 않아서 생기는 문제
ElGamal Encryption
DH과 작동 방식은 유사하다.
하지만, DH과 달리 공개키를 계속 유지하고, Ciphertext로 {C1, C2} 쌍을 생성한다.
- C1: 자신의 public key를 암호화한 것
- C2: 메시지 내용을 암호화한 것
ex) Bob이 Alice에게 메시지(M)를 보낸다.
- Bob은 랜덤한 k를 뽑는다(k: Bob's private key)
- 이 k와 Alice의 public key를 이용해 데이터를 암호화할 Key(K)를 생성한다 -> K = Ya^k mod q
- 다음의 두 값을 계산한다.
C1 = a^k mod q
C2= KM mod q - Ciphertext: {C1, C2}를 전달한다.
ex) ciphertext를 받은 Alice가 메시지를 복호화한다.
K = C1^Xa mod q
M = C2K^−1 mod q
Elliptic Curve Arithmetic
-
RSA
암호화(Encryption)와 디지털 서명(Digital signatures)을 위해 공개키 암호를 사용하는 대부분의 제품과 표준에서 RSA를 사용한다.
시간이 지날수록 RSA의 key 길이는 길어지고 있다. -
Elliptic curve cryptography(ECC): 타원 곡선 암호
ECC는 같은 안전성을 위해 필요한 key 길이가 상대적으로 짧다.
보안의 강도를 높일수록, 다른 암호들과 필요한 key의 길이 차이가 커진다.
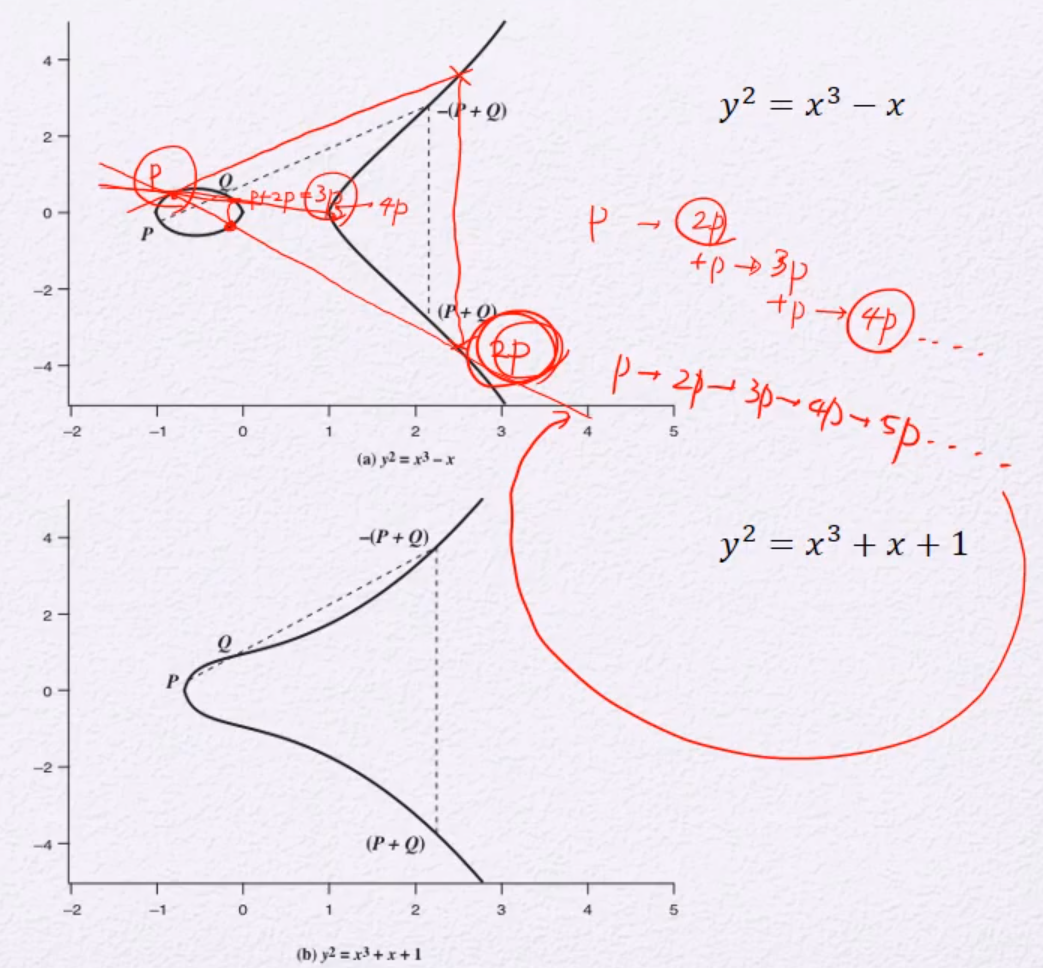
- ECC의 곱셈 연산은 modular exponentiation과 유사하다.
같은 크기의 x에서a^x = y보다xp = Q에서 x 구하는 게 훨씬 어렵다. (x가 private key 역학)
xp = Q에서 x, p를 주고 Q를 구하긴 쉽지만, p, q를 주고 x를 구하기는 어렵다
이는 Elliptic curve discrete logarithm problem(ECDLP)라고 알려져 있다.
즉, Elliptic Curve 암호의 안전성은 ECDLP의 어려움과 관련 있다.
출처
https://hororolol.tistory.com/474?category=897521
[Cryptography and Network Security: Principles and Practices]
