Public Key Cryptography
Public Key Cryptosystems의 원칙들
공개키 암호는 대칭 암호가 해결하지 못한 두 가지 문제점을 풀기 위해 시도된 암호이다.
- Key distribution
key를 어떻게 안전하게 전달 - Digital signature (Nonrepudiation)
누가 보낸 메시지인지 확인할 수 있음을 보장
Public-Key Cryptosystems
대칭키 암호에서는 하나의 key를 공유해서 사용하는 것과 달리 공개키 암호에서는 public key와 private key 두 개의 key가 존재한다.
용도에 따라 다음과 같이 작동한다.
1) 암호화 및 복호화
ex) Bob이 Alice한테 암호문을 보내려고 한다.
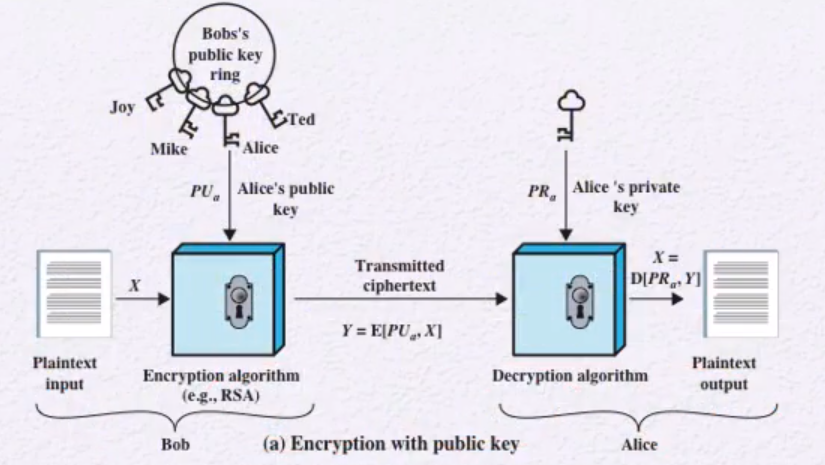
2) 서명 생성 및 확인 (Nonrepudiation)
ex) Bob이 Alice한테 계약서 보내려고 한다.
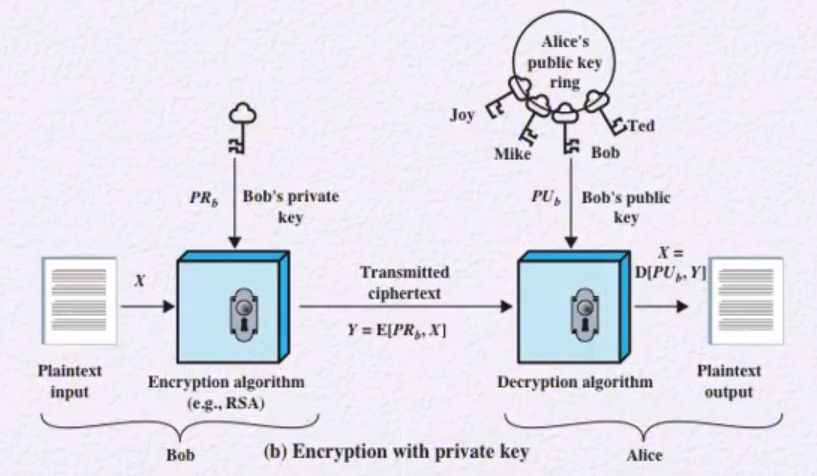
Conventional Encryption vs Public-Key Encryption
| Conventional Encryption | Public-Key Encryption | |
|---|---|---|
| 작동을 위해 필요한 것 | 1. 같은 key와 알고리즘을 사용하여 encryption/decryption한다. 2. 송수신자가 동일한 key와 알고리즘을 공유한다. | 1. 한 쌍의 key를 가지고, 하나로는 encryption, 다른 하나로는 decryption한다. 2. 송수신자는 각각 매칭되는 key쌍을 나눠가진다. |
| 보안을 위해 필요한 것 | 1. key는 비밀로 유지되야한다. 2. key만 비밀로 유지된다면 메시지 해석할 수 없어야한다. (암호 깨지지 않아야한다) 3. 알고리즘과 암호문 샘플을 알아도 key를 알 수는 없어야한다. | 1. 둘 중 하나의 key(Private key)는 비밀로 유지되어야한다. 2. Private key가 비밀로 유지되면 암호는 깨지지 않아야한다. 3.알고리즘과 암호문 샘플을 알아도 private key를 알 수 없어야 한다. |
공개키 암호: 인증(Authentication)과 기밀성(Confidentiality)
상황: Alice가 Bob한테 메시지를 보낸다고 하자.
암호문(Z) 생성: plaintext -> Alice의 private key로 암호화(인증을 위해) -> Bob의 public key로 암호화 (기밀성을 위해)
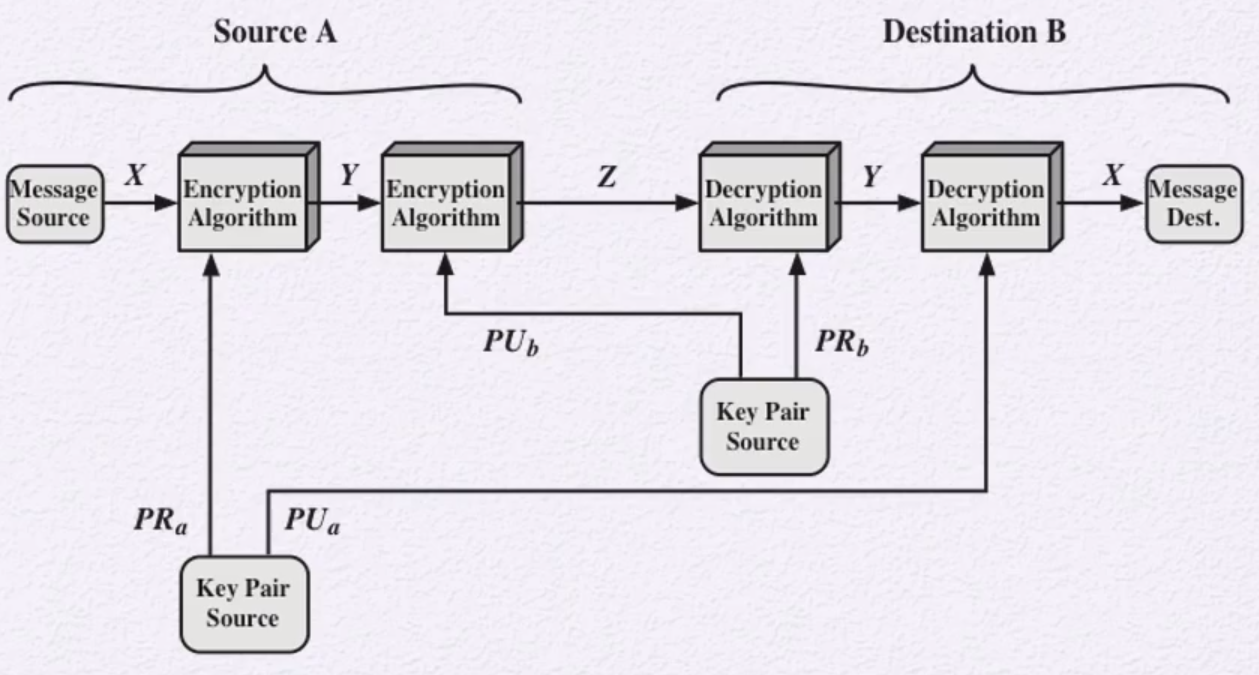
이를 해독하기 위해서는 역순으로 복호화한다.
Application
- Encryption/Decryption
송신자는 수신자의 public key로 메시지를 암호화한다. - Digital Signature
송신자는 자신의 private key로 메시지에 서명한다. - Key exchange
양측이 협력하여 세션 키를 교환한다.
| Algorithm | Encryption/Decryption | Digital Signature | Key Exchange |
|---|---|---|---|
| RSA | Yes | Yes | Yes |
| Elliptic | Curve | Yes | Yes |
| Diffie-Hellman | No | No | Yes |
| DSS | No | Yes | No |
RSA
Bit sequence를 정수로 취급해서 연산한다.
즉, 어떤 n에 대해 plaintext와 ciphertext를 0~(n-1) 사이의 정수로 표현한다.
Public-Key = {e, n}
Private-Key = {d, n}
Key Generation
- 서로 다른 소수 p,q를 선택한다.
- p,q의 곱 n을 구한다.
- Φ(n) = (p - 1) * (q - 1)을 계산한다.
- gcd(Φ(n), e) = 1 인 e를 선택한다.
- d = e^-1 mod Φ(n)을 계산한다.
긴 길이의 메시지는 어떻게 처리할까?
- Hybrid encryption
대칭 키 암호 방식을 이용하되, key를 공개키 암호를 이용하여 공유한다.
- 작동 방식
암호 메시지를 보낼때 {C1, C2} 두 개를 보낸다.
C1: 암호화된 문서
C2: 암호화된 Key(K^e mod n)
ex) Alice가 Bob에게 메시지를 보낸다고 하자.
1. Alice는 문서를 암호화할 key를 랜덤하게 생성한다.
2. 그 key로 문서를 암호화한다. -> C1 생성
3. 그 후, 해당 key를 Bob의 public key로 암호화한다. -> C2 생성
4. 이렇게 생성된 {C1, C2}를 Bob에게 전송한다.
5. Bob은 자신의 private key로 C2를 복호화해 key를 얻는다.
6. 복호화한 key로 C1을 복호화해 plaintext를 얻는다.
Why?
메시지가 길어지면, 메시지를 여러 개의 블락으로 나눠야 하고, 암호화 알고리즘을 여러 번 거쳐야 한다.
이때, 공개키 암호 알고리즘은 성능이 안 좋기 때문에 느리다.
그래서 빠른 대칭키 암호로 많은 양을 암호화시켜 속도를 향상하고,
대신 대칭 키 암호에는 안전하게 key를 공유하는데 안전성 문제가 있을 수 있으므로, 공개키 암호를 사용해 안전성을 높였다.
RSA 서명
ex) Alice가 Bob에게 계약서를 보낸다고 하자.
1. Signature(S) = M^d mod n
2. Alice의 private key = {d, n}
3. Alice의 public key = {e, n}
4. Alice는 Bob에게 {M, S} 쌍을 보낸다. -> {메시지, 서명}
5. Bob은 계약서를 받고 서명(S)을 Alice의 public key를 이용해 복호화해본다 -> M = S^e mod n
6. 이 작업을 통해 Integrity, Authentication, Nonrepudiation을 모두 보장할 수 있다.
RSA 공격
- Brute force
다 해보기 -> 경우의 수가 너무 많아서 거의 불가능 - Mathematical attacks
factor n (n!) 해보기
정수를 소인수 분해만 쉽게 하면 RSA는 깨질 수 있다. - Chosen ciphertext attack
- Implementation attacks
값마다 알고리즘의 연산량이 다름을 이용 -> 시간 차이, 전략 사용량 차이 등
Mathematical attacks(Factoring Problem)
RSA를 수학적으로 공격하기 위한 접근법 3가지
-
RSA에서 ø(n) = (p-1)*(q-1) 연산하는 부분이 있다.
소인수 분해를 효율적으로, 빨리 할 수 있으면, d = e^−1 (mod ø(n))을 결정할 수 있다. -
소인수 분해 하지 않고 바로 ø(n) 구하기
-
ø(n) 구하지 않고 바로 d 구하기
Factoring을 쉽게 하면 RSA는 깨진다. Factoring이 RSA의 안전성이라고 생각할 수 있다.
Chosen Ciphertext Attack(CCA)
-
공격자가 ciphertext를 선택한다.
-
선택한 ciphertext에 대해서 private key를 가진 사람한테 decryption 요청
-
그 결과 공격자는 {Ciphertext, Plaintext} 쌍을 얻게 된다.
-
공격자가 이전에 선택한 Ciphertext 이외의 것을 한 개라도 복원하면 공격자 승리
Implementation Attack: Side Channel Attacks
알고리즘이 작동되면서 생성되는 부수적인 정보들을 이용해 공격하는 방법이다.
-
Timing attack
private key에 따라 연산 시간이 달라지는 점을 활용.
정수 값에 따라 알고리즘을 돌렸을 때, 걸리는 시간이 다른데, 이런 부분을 이용 -
Power analysis, Electromagnetic analysis, Cache 등
값에 따라 연산을 수행할 때 사용되는 전력 양 등이 다름을 이용
Fault-Based Attack
연산이 수행되는 와중에 갑자기 강력한 전압을 걸거나 해서 의도적으로 에러를 유도한다.
정상 결과와 비정상 결과를 모두 얻은 후, 이를 조합해서 추가적인 정보를 얻어낸다.
공개키 암호에 대한 오해
-
공개키 암호는 대칭 암호보다 안전하다?
암호화 방식 자체가 달라서 그렇다고 얘기할 수 없다. -
공개키 암호는 대칭 암호를 완전히 대체할 수 있다?
성능 자체는 대칭 암호가 훨씬 좋다. 그래서 보통 둘을 섞어서 사용하는 Hybrid 방식을 사용한다. -
공개키 암호는 키 공유 문제가 전혀 없는가?
상대적으로 나은 것이지, 그 문제가 근본적으로 해결된 것은 아니다.
대칭 암호는 기밀성이 보장된 상태, 공개키 암호는 무결성과 인증이 보장된 상태로 키 분배해야한다.
출처
https://hororolol.tistory.com/472?category=897521
[Cryptography and Network Security: Principles and Practices]
