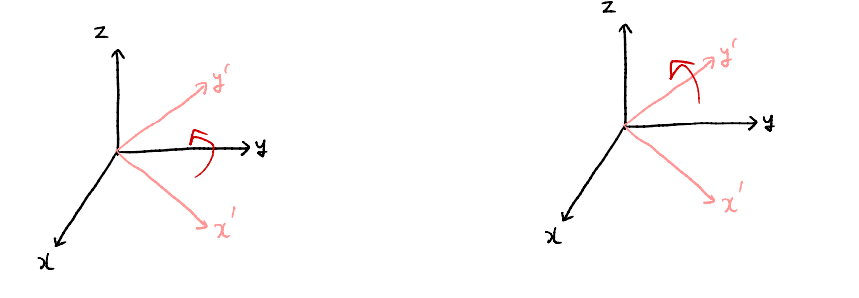오일러 각
- 3차원 물체의 방향(orientation)을 3개의 서로 수직인 X,Y,Z축 각도로 표현하는 방법
- 3차원 공간에 놓인 기체의 방향은 오일러 각도를 사용하여 3번의 순차적인 회전을 통해 얻을 수 있고, 3개의 축은 서로 종속적인 관계임
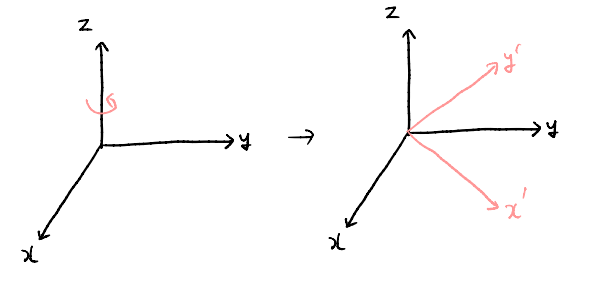
Fixed-Angle와 비교
- Fixed-Angle vs Euler-Angle
오일러 각도를 회전행렬로 변환
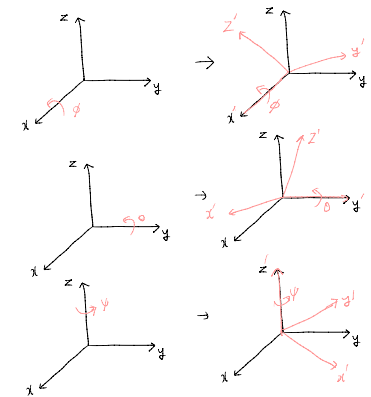
Rot(xˊ,ϕ)= ⎣⎢⎡1000cosϕsinϕ0−sinϕcosϕ⎦⎥⎤
Rot(yˊ,θ)= ⎣⎢⎡cosθ0−sinθ010sinθ0cosθ⎦⎥⎤
Rot(zˊ,ψ)= ⎣⎢⎡cosψsinψ0sinψcosψ0001⎦⎥⎤
오일러 각도의 표현
RZYX(ϕ,θ,ψ)=Rot(zˊ,ψ)Rot(yˊ,θ)Rot(xˊ,ϕ)
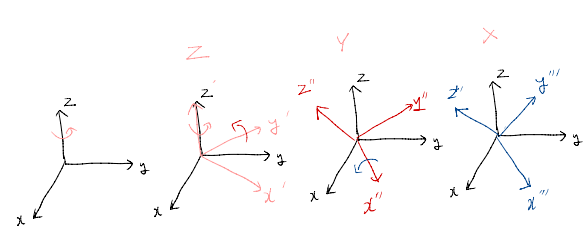
참고
https://edward0im.github.io/engineering/2019/11/12/euler-angle/
https://m.blog.naver.com/droneaje/221999534231