칼만필터

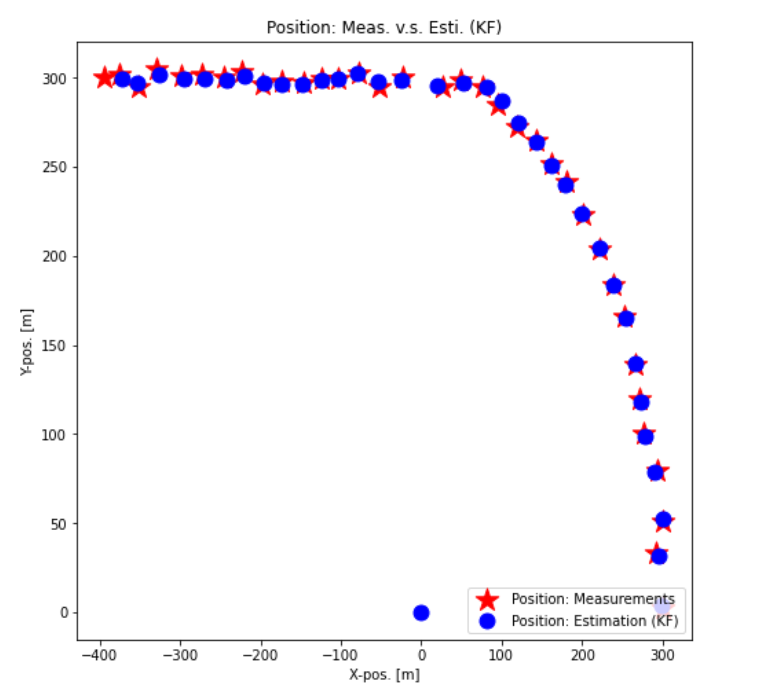
1. 칼만 필터 알고리즘

• 입력과 출력이 하나씩인 아주 간단한 구조
• 측정값($z^k$)이 입력되면 내부에서 처리한 다음, 추정값($\hat{x_k}$)을 출력
  

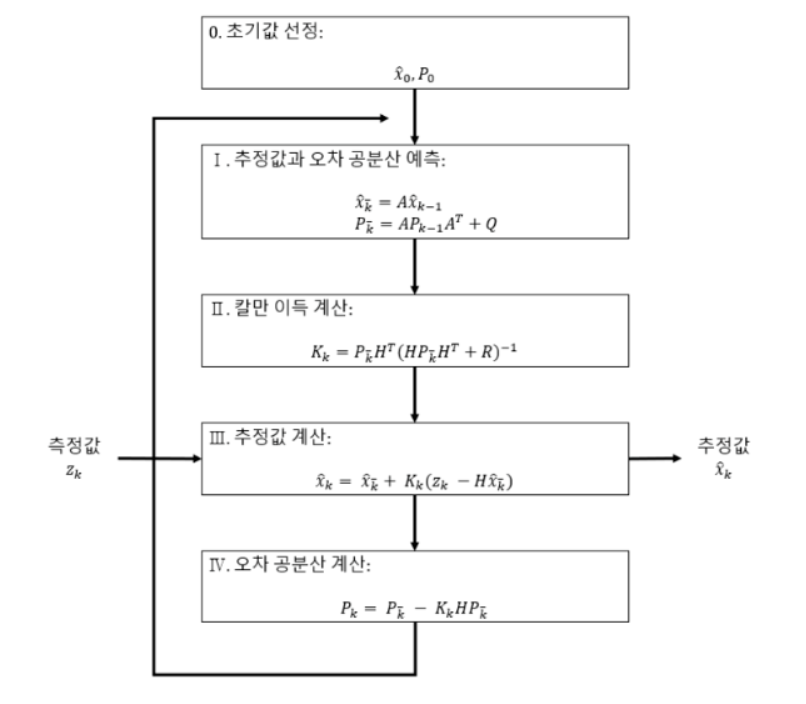
2. 칼만 필터 알고리즘의 계산 과정

1단계 : 추정값과 오차 공분산 예측

• 추정값의 예측값($\hat{x_k^-}$)과 오차 공분산의 예측값($P_k^-$)을 계산
• 예측 단계의 계산식은 시스템 모델과 밀접하게 관련

2단계 : 칼만 이득 계산

• 칼만 이득($K_k$)을 계산한다. 오차 공분산의 예측값($P_k^-$)이 계산에 들어감
  H, R은 시스템 모델과 관련된 변수

3단계 : 입력된 측정값으로 추정값 계산

• 이 단계의 계산식은 저주파 통과 필터와 관련이 있음. 추정값의 예측값($\hat{x_k^-}$)이 계산에 들어감

4단계 : 오차 공분산 계산

• 오차 공분산은 추정값이 얼마나 정확한지를 알려주는 척도로 사용

알고리즘에 등장하는 변수

시스템 모델 변수는 설계자가 사전에 확정하는 값이고 나머지 변수들은 설계자가 임의로 변경할 수 없음. 측정되거나 알고리즘에서 계산하는 값

변수용도	변수
외부 입력	$z^k$(측정값)
최종 출력	$\hat{x_k}$(추정값)
시스템 모델	A, H, Q, R
내부 계산용	$\hat{x_k^-}$,$P_k^-$,$P_k$,$K_k$

의미를 기준으로 나눔

예측과정(predict)

• 칼만 필터 알고리즘의 1단계
• 직전 추정값($\hat{x_{k-1}}$), 직전 오차 공분산($P_{k-1}$)->예측값($\hat{x_k^-}$,$P_k^-$)
• 시스템 모델 변수 A,Q 사용

추정과정(update)

• 칼만 필터 알고리즘의 2, 3, 4단계
• 예측 과정의 예측값($\hat{x_k^-}$,$P_k^-$), 측정값($z_k$) -> 추정값($\hat{x_k}$), 오차 공분산($P_k$)
• 시스템 모델 변수 H,R 사용

3. 추정과정

3.1 칼만 이득 계산

• 가중치 $K_k$ 는 알고리즘을 반복하면서 계속 변함
• $K_k=P_k^- H^T(HP_k^-H^T+R)^{-1}$

3.2 추정값 계산

• $\hat{x_k}$=(I-$K_k$)$\hat{x_k^-}$+$K_kz_k$ (H 단위행렬 가정)

3.3 오차 공분산($P_k$) 계산

• 추정값이 정확한지 아닌지를 오차 공분산($P_k$)으로 판단 가능
• ($P_k$)가 크면 추정 오차가 크고, ($P_k$)가 작으면 추정 오차도 작음

4. 예측 과정

4.1 예측값 계산

• 추정값을 예측하는 식
  $\hat{x_{k+1}^-} = A\hat{x_k}$
• 오차 공분산을 예측하는 식
  $P_{k+1}^-=AP_kA^T+Q$
• 예측값을 추정값 계산식에 대입
  $\hat{x_k}=A\hat{x_{k-1}}+K_k(z_k-HA\hat{x_{k-1}})$

4.2추정값 계산식의 재해석

• 칼만 필터는 측정값의 예측 오차로 예측값을 적절히 보정해서 최종 추정값을 계산
  $\hat{x_k}=\hat{x_k^-}+K_k(z_k-H\hat{x_k^-})$
• $H\hat{x_k^-}$ -> 예측값으로 계산한 측정값
• $z_k-H\hat{x_k^-}$ -> 실제 측정값과 예측한 측정값의 차이, 측정값의 예측 오차

칼만 필터의 성능은 시스템 모델에 달려있음

칼만 이득은 예측값을 얼마나 보정할지 결정하는 인자가 된다.
- 칼만 이득이 크면?
- 칼만 이득이 작으면?
추정값 계산식을 예측값의 보정 관점에서 보면,추정값의 성능에 가장 큰 영향을 주는 요인은 예측값의 정확성. 예측값이 부정확하면 아무리 칼만 이득을 잘 선정한다고 해도 추정값이 부정확할 수 밖에 없기 때문! 예측값에서 사용되는 변수는 추정값과 시스템 모델 A, Q이므로 칼만 필터의 성능은 시스템 모델에 달려있다고 할 수 있음

5. 시스템 모델

5.1 시스템 모델

칼만 필터는 아래와 같은 선형 상태 모델을 대상으로 함

• $x_{k+1}=Ax_k+w_k$
• $z_k=Hx_k+v_k$
  시스템의 운동 방정식(A)을 상태 변수 벡터($x_k$)에 대해 1차 차분(또는 미분) 방정식으로 표현한 모델을 상태 공간(state space) 모델이라고 함

$x_k$ : 상태 변수, (n x 1) 열벡터
상태 변수는 거리, 속도, 무게 등 우리가 관심 있는 물리적인 변수로 이해하면 쉽다.
A : 시스템 행렬, (n x n) 행렬
시간에 따라 시스템이 어떻게 움직이는지를 나타낸다. 시스템의 운동 방정식
$w_k$ : 시스템 잡음, (n x 1) 열벡터
시스템에 유입되어 상태 변수에 영향을 주는 잡음.
$z_k$ : 측정값, (m x 1) 열벡터
H : 출력 행렬, (m x n) 행렬
측정값과 상태 변수의 관계
$v_k$ : 측정 잡음 , (m x 1) 열벡터
센서에서 유입되는 측정 잡음.
-> 칼만 필터에서는 잡음이 중요한 역할을 하는데, 모든 잡음을 백색 잡음으로 가정한다.
(백색 잡음 : 모든 주파수 성분을 다 갖고 있는 잡음)

• 칼만 필터 알고리즘에서 시스템 모델과 관련 있는 부분
  1단계의 추정값 예측식 & 3단계의 추정값 계산식

5.2 잡음의 공분산

• 잡음 신호는 다음에 어떤 값이 나올지 예측할 수 없기 때문에 순전히 통계적인 추정만 가능
• 칼만 필터는 잡음의 평균이 0인 정규분포를 따른다고 가정하기 때문에, 잡음의 분산만 알면 됨
• 칼만 필터는 상태 모델의 잡음을 다음과 같은 공분산 행렬(변수의 분산으로 구성된 행렬)로 표현

Q:$w_k$ 의 공분산 행렬, (nxn) 대각행렬
R:$v_k$ 의 공분산 행렬, (mxm) 대각행렬

• n개의 잡음 $w_1,w_2,...,w_n$ 이 있고, 각 잡음의 분산은 $\sigma_1^2,\sigma_2^2,...,\sigma_n^2$ 이라고 하면 공분산 행렬 Q는
  
• 측정 잡음 $v_k$의 공분산 행렬 R도 같은 방식으로 구성
• 행렬 Q와 R은 잡음의 특성을 정확히 반영해서 구성하는 게 원칙이지만, 여러 오차가 복합적으로 작용하기 때문에 해석적으로 결정하는 데는 한계가 있음
• 따라서 해당 시스템에 대한 경험을 바탕으로 어느 정도의 시행착오를 겪을 수 밖에 없음

5.3 적절한 기준 존재?

• 칼만 이득($K_k$)
  $\frac{P_K^-H^T}{HP_k^-H^T+R}$
• 오차 공분산의 예측값($P_k+1^-$)
  $P_{k+1}^-=AP_kA^T+Q$
  => 행렬 R↑ , 칼만 이득($K_k$)↓
  => 행렬 Q↑, 오차 공분산 예측값($P_{k+1}^-$)↑,칼만 이득($K_k$)↑
  => 칼만 이득이 작아지면 측정값이 덜 반영되고, 칼만 이득이 커지면 측정값이 더 많이 반영

코드로 적용

def kalman_filter(z_meas, x_esti, P):
    """Kalman Filter Algorithm."""
    # (1) Prediction.
    x_pred = A @ x_esti
    P_pred = A @ P @ A.T + Q

    # (2) Kalman Gain.
    K = P_pred @ H.T @ inv(H @ P_pred @ H.T + R)

    # (3) Estimation.
    x_esti = x_pred + K @ (z_meas - H @ x_pred)

    # (4) Error Covariance.
    P = P_pred - K @ H @ P_pred

    return x_esti, P
    
# Initialization for system model.
# Matrix: A, H, Q, R, P_0
# Vector: x_0
A = np.array([[1, dt, 0.5**dt, 0, 0, 0],
              [0,  1, dt,  0, 0, 0],
              [0, 0, 1, 0, 0, 0],
              [0, 0, 0, 1, dt, 0.5**dt],
              [0, 0, 0, 0 , 1, dt],
              [0, 0, 0, 0, 0, 1]])
H = np.array([[1, 0, 0, 0, 0, 0],
              [0, 0, 0, 1, 0, 0]])
Q = np.array([
    [0.25, 0.5, 0.5, 0, 0, 0], 
    [0.5, 1, 1, 0, 0, 0], 
    [0.5, 1, 1, 0, 0, 0], 
    [0, 0, 0, 0.25, 0.5, 0.5],
    [0, 0, 0, 0.5, 1, 1],
    [0, 0, 0, 0.5, 1, 1]
])
R = np.array([[9,  0],
              [0, 9]])

# Initialization for estimation.
x_0 = np.array([0, 0, 0, 0, 0, 0])  # (x-pos, x-vel, y-pos, y-vel) by definition in book.
P_0 = 500 * np.eye(6)

더 자세한 코드