Abstract

• 복잡한 시간적 의존성과 제한된 label로 인해 Time series Anomaly detection(TSAD)은 어려움. 기존 모델과 딥러닝 기반 모델을 포함한 일부 알고리즘들이 제안되었지만, 대부분은 시간 영역의 모델링에만 초점을 맞추고, 시계열 데이터의 Frequency 영역 정보를 충분히 활용하지 못하고 있음. 본 논문에서는 성능 향상을 위해 시간 및 Frequency 영역을 모두 활용하는 TFAD (Time-Frequency analysis based time series Anomaly Detection)을 제안함
• 또한, 설계된 모델의 구조에서 시계열 분해 및 data augmentation을 통합적으로 수행하여 성능 및 해석 능력을 더욱 향상시킴

Introduction

• IoT 시스템과 기타 모니터링 시스템의 발전으로 시계열 데이터의 양이 크게 증가했으며 이에 따라 시계열 데이터에서 이상 또는 특이점을 효과적으로 모니터링하고 탐지하는 것은 실제 응용 분야에서 결함을 발견하고 잠재적 위험을 방지하는 데 중요함
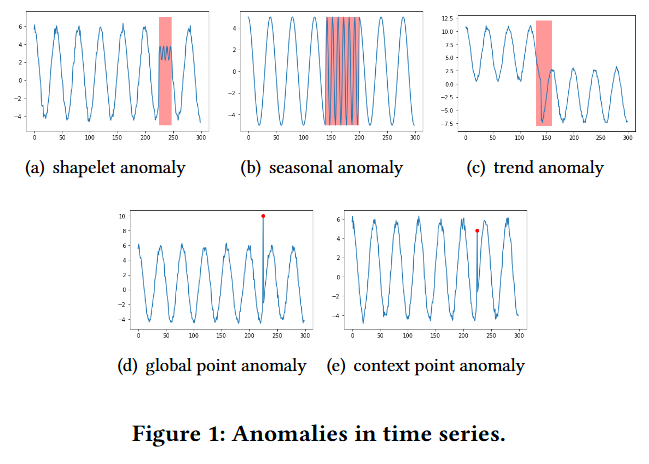
• 일반적인 Tabular data가 아닌, 시계열 데이터의 가장 큰 특징 중 하나는 시간적 의존성임. 일반적으로 시계열의 특정 시점이나 부분 시퀀스는 해당 'context'와 비교했을 때 이상치로 간주됨. 시계열 데이터에서는 아래 그림과 같이 다양한 유형의 이상치를 정의할 수 있기 때문에 시계열 이상 탐지에서 첫 번째 Challenge는 다양한 유형의 이상치에 대해 특정 시점/부분 시퀀스와 시간적 context 간의 관계를 모델링하는 방법임

• 두 번째 Challenge는 이상치는 드물게 발생하기 때문에 label 부족 문제를 해결해야 하며, Data augmentation으로 문제를 해결하려는 연구가 다수 진행되었지만 시계열 데이터에 augmentation을 수행하는 방법에 대해서는 여전히 해결해야할 문제로 남아있음
• 시계열 데이터는 시간 영역뿐만 아니라 주파수 영역에서도 분석될 수 있으며 기존의 연구들에서는 주파수 영역의 정보를 충분히 활용하지 않음. 최근에는 주파수 영역에서의 데이터 증강과 같은 방식으로 시계열을 모델링하려는 시도가 이루어지고 있으나 시계열 이상 탐지에서 시간 영역과 주파수 영역의 정보를 동시에 체계적이고 직접적으로 활용하는 방법은 충분히 탐구되지 않음
• 본 논문에서는 다양한 유형의 이상치를 더 잘 감지하기 위해 시간-주파수 영역에서 이상 탐지를 수행하는 TFAD를 제안함.

Proposed Method

Time-Frequency Analysis

Uncertainty Principle for Time series Representation in Time & Frequency Domains

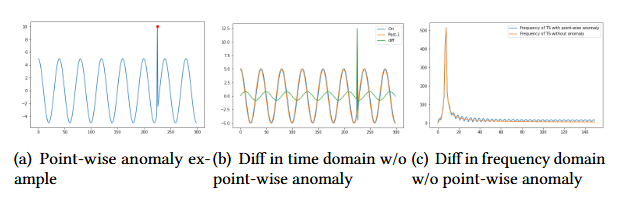
• 시계열 분석 분야에서 사용되는 불확정성 원리는 기본적으로 연속 함수의 표준 편차와 푸리에 변환의 표준 편차 사이의 기본적인 관계를 의미함. 이는 Schwarz 부등식에 의해서 결론을 이끌어낼 수 있는데, 간단하게 말하자면 하나의 모델이 시간 영역에서 Point-wise anomaly를 잘 잡아낼 경우에 주파수 영역에서는 감지 능력이 떨어지는 것을 의미함
• 따라서, 시간 및 주파수를 동시에 감지할 수 있는 단일 구조의 모델을 설계하는 것은 어려우며 서로 다른 구조를 사용하여 각각의 영역을 감지하고 전체 모델로 병합하는 것이 더 나은 접근 방식이라고 생각함

Understanding the Limitations of Single Domain Analysis

• Point-wise anomaly 감지와 Pattern-wise anomaly 감지의 중요한 차이점을 보이고, 시간 또는 주파수 영역에서만 이상을 감지하는 것의 한계를 설명하려 함.

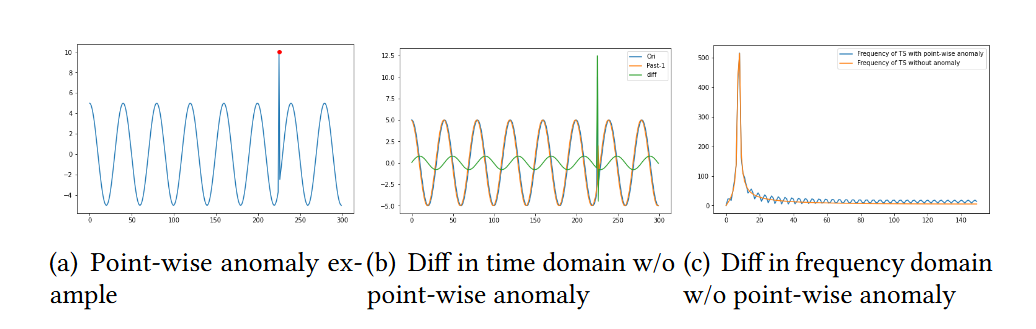
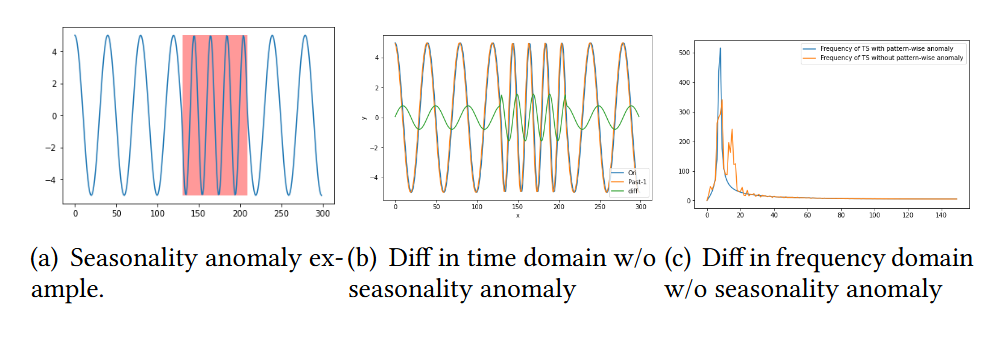
• 위 그림에서 첫번째 행은 Global point anomlay의 예시 ((a)그림)을 통해 시간 영역과 주파수 영역에서 point-wise anomaly를 감지하는 것의 차이점을 보여주고, 두번째 행은 시간 영역에서 pattern wise anomaly를 감지하는 것의 차이점을 보여줌
• 일반적으로 시간 영역에서의 이상 탐지는 특정 시점의 데이터를 과거의 이웃 데이터와 비교하여 수행되는데, 위 그림의 두 번째 열을 통해 시간 영역의 분석에서는 point-anomaly가 seasonality anomaly보다 더 쉽게 탐지될 수 있음을 알 수 있고 시간 영역에서의 분석만으로는 seasonality anomaly를 탐지하는 것은 쉽지 않다는 것을 알 수 있음
• 주파수 영역에서의 이상 탐지는 Fourier transform 후 비교를 수행함. 위 그림의 세 번째 열을 통해 주파수 영역의 분석에서는 Seasonality anomaly가 point-anomaly보다 더 탐지 쉽다는 것을 알 수 있음

Data Augmentation and Decomposition

Time series data Augmentation

• 일반적으로 ML의 성능은 많은 학습데이터에 의존하지만 현실에서는 labeled data가 부족한 경우가 많음. Data augmentation은 이러한 문제들을 완화하는 데 크게 기여함. 대부분의 기존 연구에서는 증강된 데이터가 원본 데이터 분포를 따라야 한다고 보지만, 본 논문에서는 이상 탐지 작업을 위해 정상 데이터 증강과 이상 데이터 증강, 이 두 가지 종류의 데이터 증강 방법을 고려함. 이상 데이터는 다양한 유형이 존재하므로 실제 이상과 동일한 이상을 생성할 필요는 없고 비현실적인 증강이기 때문에 다양한 이상 데이터를 증강하며 이는 모델의 Robustness를 올리는 데 기여함

Time series Decomposition

• 일반적으로 시계열 데이터는 다양한 패턴을 나타내기에 시계열의 주요 구성 요소로 분해하는 방식이 유용한 경우가 많음. 이는 시계열 이상 감지 및 예측에 널리 사용되는 복잡한 시계열 분석을 위한 접근 방식임

High level Architecture of TFAD

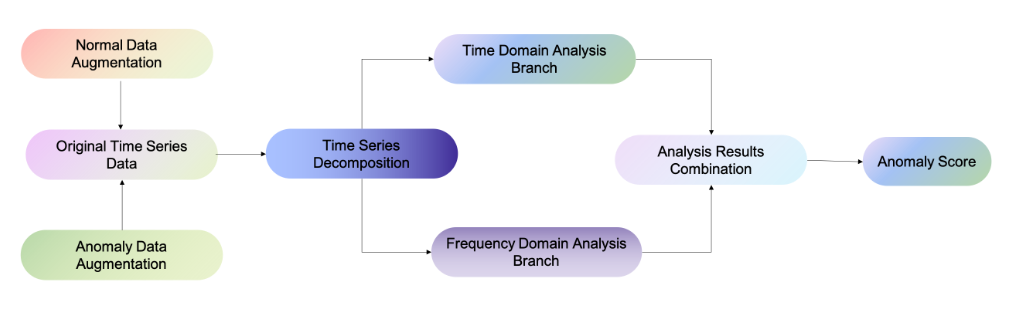
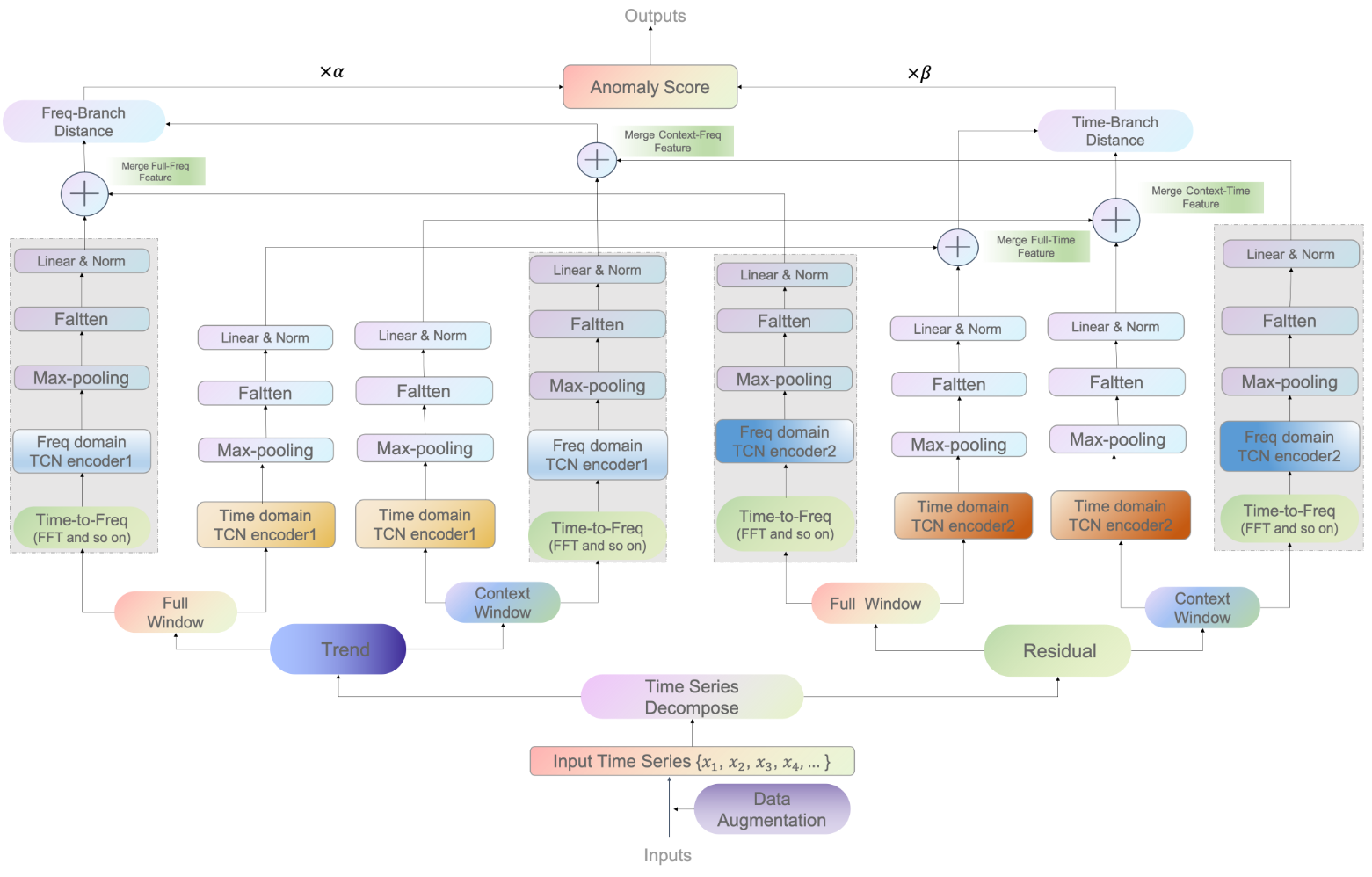
• 앞서 언급된 Augmentation, 시간-주파수 영역의 분석, Decomposition 등의 필요성에 의해 설계된 TFAD 알고리즘의 상위 레벨의 구조를 위 그림을 통해 확인할 수 있음
• TFAD는 시간 영역 분석 branch와 주파수 영역 분석 branch, 이렇게 두 가지 주요 branch로 구성됨. 이외에도 Normal data Augmentation module과 Anomaly data Augmentation module은 TFAD의 Robustness를 높이기 위해서 설계되었음. 추가적으로 Decomposition module은 여러 구성 요소에서 이상치를 더 잘 감지하고 감지된 이상에 대한 Insight를 제공하기 위해 설계됨

Network Design of TFAD

Data Augmentation module

• 해당 모듈에서는 정상과 이상 데이터를 모두 증강하는 접근 방식을 취함. 정상 데이터 증강을 위해 우선 노이즈가 적은 데이터를 생성하며 이는 정상보다 더욱 정상같은 데이터임. 이를 위해 본 논문에서는 Robust STL을 활용하여 noise를 제거하는 방식으로 노이즈가 적은 데이터를 생성함
• 또한, 다양한 정상 데이터를 생성하기 위해 시계열을 Fourier transform을 통해 주파수 영역으로 변환하고 허수 및 실수 부분 모두에 변화를 주어 새로운 데이터를 얻음. 이러한 주파수 영역에서의 변환은 아래 그림의 예시를 통해 살펴볼 수 있음

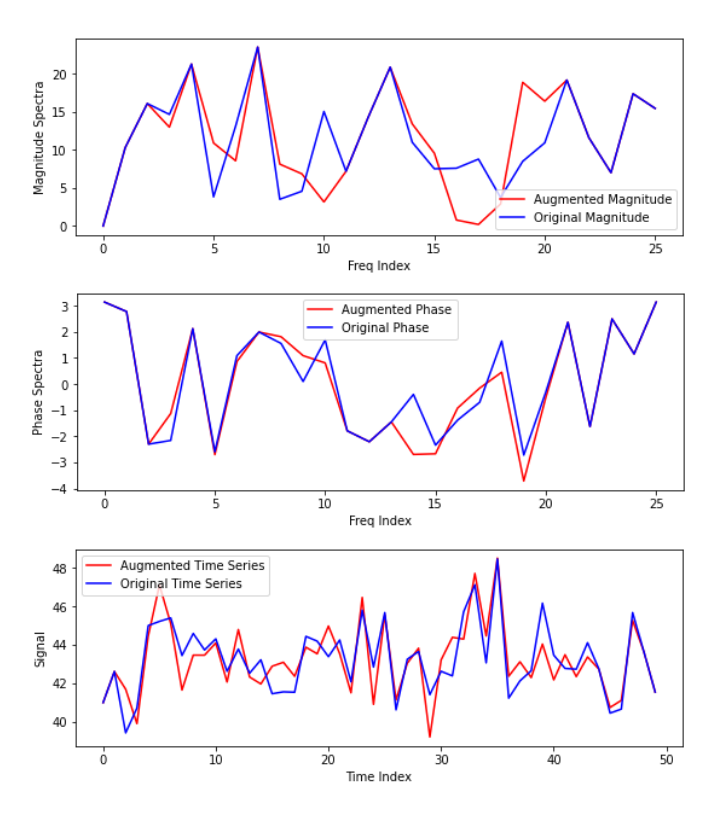
• 정상 데이터 이외에 이상 데이터를 생성할 때, 데이터셋에 포함된 전형적인 이상치 외에도 다른 잠재적인 이상치 또한 고려해야 함. 이를 위해 point scale 조정, mix-up, Frequency domain 증강 기법 등 다양한 형태의 이상을 생성함

Decomposition module

• 본 논문에서는 시계열 분해를 위해 Hodrick-Prescott filter를 사용하였음. 이는 구현이 용이하고 실제 환경에서 잘 작동하는 방법임.

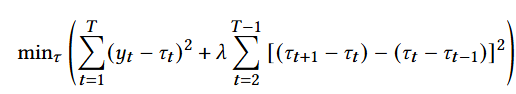
• 시계열이 추세 ($\tau_t$)와 잔차($\epsilon_t$) component를 포함한다고 할때, HP filter에서 추세 component는 위 수식을 최소화함으로 써 얻을 수 있음. 여기서 $\lambda$는 추세의 변동에 대한 민감도를 조정하는 매개변수이며 관측 빈도에 따라 조정할 수 있음. 분해 결과로 얻어진 추세 및 잔차는 모두 모델의 성능을 개선시키기 위한 추수 과정에 사용됨
• 단, 본 논문에서는 주로 단변량 시계열을 대상을 분해 방법을 고려했다는 한계가 있음

Window splitting module

• 해당 모듈은 sequence 별/ 시간적 상관관계 정보를 더 잘 얻기위해 채택하였으며, 구체적으로 전체 시계열 window와 context 시계열 window가 의심스러운 sequence의 anomaly를 감지하기 위해 설정되며, 전체 window는 context window와 의심스러운 window로 구성됨. 이때, context window가 정상이라고 가정함

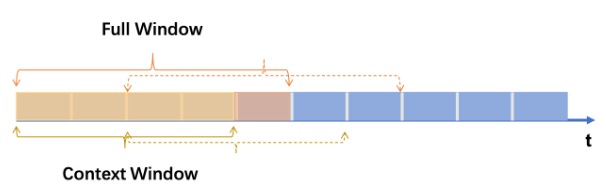
Time and Frequency Branches

• 원본 시계열이 Trend 및 잔차로 분해되고 각 구성 요소에 대해 앞서 언급한 window splitting을 사용하여 full window와 context window를 설정함. 그런 다음, 각 window에 대해 time-domain representation learning과 frequency-domain representation learning을 수행하여 sequence에 대한 풍부한 정보를 얻음. 그 후, context window와 full window 사이의 거리를 측정하여 anomaly score를 계산함

• 거리를 측정할 때 Cosine distance나 DTW와 같은 전통적인 거리 측정 방법들은 시계열 길이에 지나치게 민감하여 적용하기 어려움. 따라서 본 논문에서는 이러한 방법들의 단점을 극복하기 위해 신경만 기반의 network를 사용함. 구체적으로, Temporal Convolutional Network(TCN)을 표현 네트워크로 활용함

• 또한, 본 논문에서 주파수 영역에서의 분석을 위해 Discrete Fourier Transform (DFT)를 사용하여 Time domain에서 주파수 영역으로 변환을 수행함. 이는 다른 CFT, STFT와 같은 알고리즘보다 비교우의를 가지기 때문에 DFT를 활용함

Anomaly Score module

• TFAD의 anomaly score는 아래 수식을 통해 계산됨

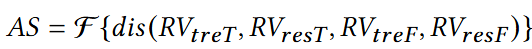
• 여기서 $RV_{treT}$와 $RV_{resT}$는 각각 시간 영역에서 Trend와 Residual 성분의 표현 결과이고, $RV_{treF}$와 $RV_{resF}$는 각각 주파수 영역에서 Trend와 Residual 성분의 표현 결과임. 이때 거리를 계산하는 과정에서는 Cosine similarity가 사용됨. Anomaly score가 높다는 것은 의심 구간이 비정상일 가능성이 높다는 것을 뜻함.

• 구체적으로, Full window와 Context window를 sliding 하는 과정에서 의심 구간도 같이 sliding되는데 이때 모든 지점은 여러 의심 구간에 속하게 되고 그 중 절반 이상이 anomaly로 labeling이 된다면 해당 지점이 anomaly로 판단되는 프로세스를 거침

Experiments

Performance Comparisons

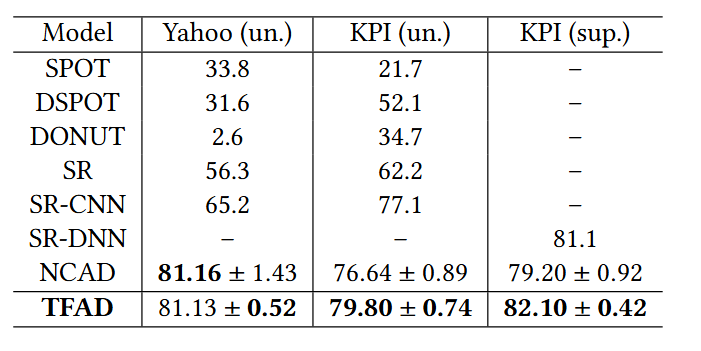
• 위 표에 나타낸 단변량 시계열 이상 탐지의 경우, 딥러닝 기반 방법론들이 SPOT 및 DSPOT와 같은 기존의 Threshold 기반 방버보다 일반적으로 더 나은 성능을 나타내는 것을 알 수 있음
• NCAD와 TFAD는 모두 Data Augmentation을 도입한 방법론이지만 TFAD의 분산은 대부분의 경우 NCAD보다 현저히 낮으며, 이는 TFAD 방법론이 실제 시스템에서 더 강력하고 안정적임을 나타냄

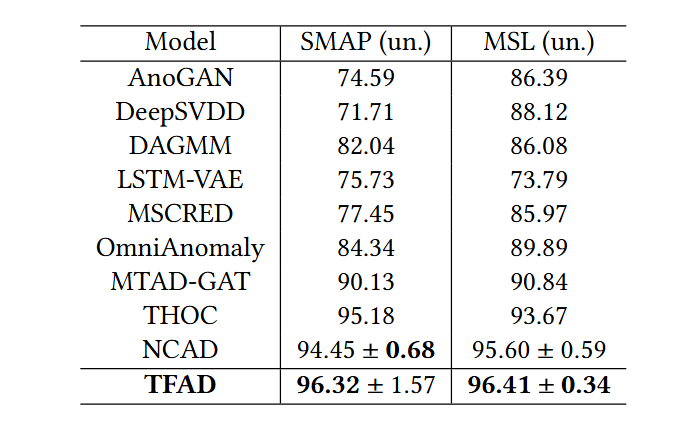
• 또 다른 실험으로 위 표에 나타낸 다변량 시계열 이상 탐지의 성능 비교 결과를 보면, TFAD가 THOC와 NCAD 등의 최신의 방법의 성능을 넘어선 결과를 볼 수 있으며 이는 기존 연구들이 시간 영역에서만 이상을 탐지하는 반면, TFAD는 시간 영역과 주파수 영역을 모두 갖춘 새로운 구조를 사용했기 때문으로 저자들은 설명하고 있음

Ablation studies

1. Time branch나 Frequency branch만 사용할 경우, 모델의 성능이 하락함
2. Time branch에 Decomposition module을 추가하면, 동일한 TCN model에 비해 F1 score가 거의 30% 향상됨
3. Augmentation data rate가 0.5로 설정된 Normal data augmentation module을 추가하면 추가적인 성능 향상을 얻을 수 있음. 이러한 성능 개선은 Time-domain 이상 데이터 증강 module을 추가하고 augmentation ratio를 0.4로 설정했을 때도 동일함. 특기할만한 부분은 각 module을 추가했을 때의 성능 향상폭의 합보다 두 module을 동시에 추가했을 때 성능 향상폭이 더 크다는 것임
4. Frequency branch를 추가한 뒤, F1 score가 향상될 뿐만 아니라 Variance도 줄어드는 결과를 얻을 수 있음

Model Analysis and Dicussion

Contribution of time series decomposition module

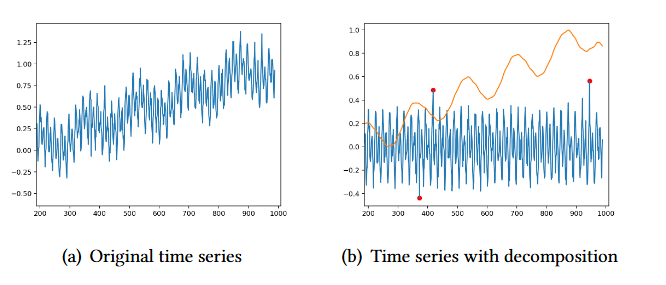
• 위 그림은 Yahoo dataset의 예시로, Time series decomposition의 효과를 살펴볼 수 있음

Adaptive window size

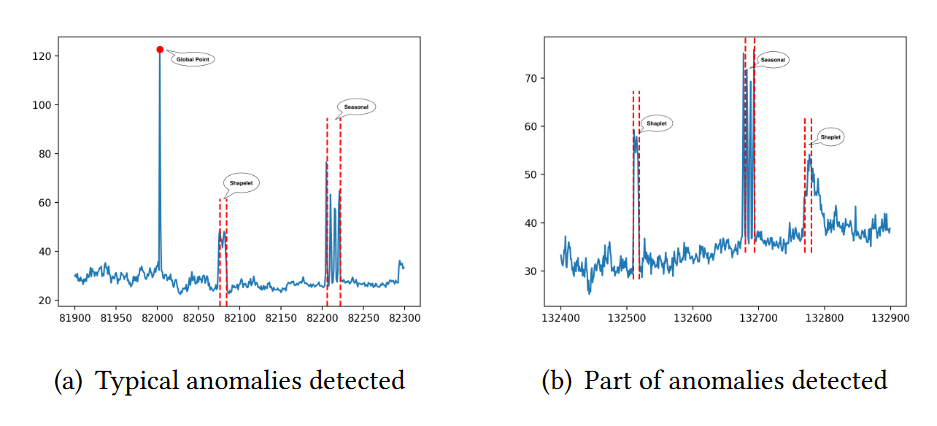
• 위 그림은 TFAD에 의해 감지된 몇 가지 일반적인 이상을 나타낸 것임. (a)는 point, shapelet, seasonal anomaly를 포함한 모든 이상이 탐지되었으나, (b)는 가장 오른쪽에 있는 하위 sequence 중 일부가 효과적으로 감지되지 않는 현상이 나타남
• 이는 중간 및 오른쪽 부분 이상이 서로 가깝고 중간 부분의 이상이 오른쪽 부분의 이상보다 더 두드러지기 때문에 의심 구간을 테스트할 때 중간 부분의 이상은 full window와 context window의 표현을 크게 변경하여 오른쪽 부분의 의심 구간에서 이상을 숨기게 됨. 이러한 문제는 동일한 window size를 적용하기 때문에 발생하는 것으로 이를 극복하기 위한 Adaptive window size에 관한 연구는 향후 연구에 진행할 것임을 저자들은 밝힘

Conclusion

• 본 논문에서는 시계열 이상 탐지를 위한 시간-주파수 분석 기반 모델을 제안함. 해당 모델은 시간-주파수 영역의 특성을 파악하는 연구로, labeled data의 부족 문제를 해결하기 위해 Data augmentation을 활용함
• TFAD는 복잡한 신경망 구조를 활용하지 않고 TCN 구조를 활용함에도 기존 딥러닝 모델보다 더 나은 성능을 얻음