신장 트리
그래프에서 모든 노드를 포함하면서 사이클이 존재하지 않는 부분 그래프
모든 노드가 포함되어 서로 연결되면서 사이클이 존재하지 않는다는 조건은 트리의 조건

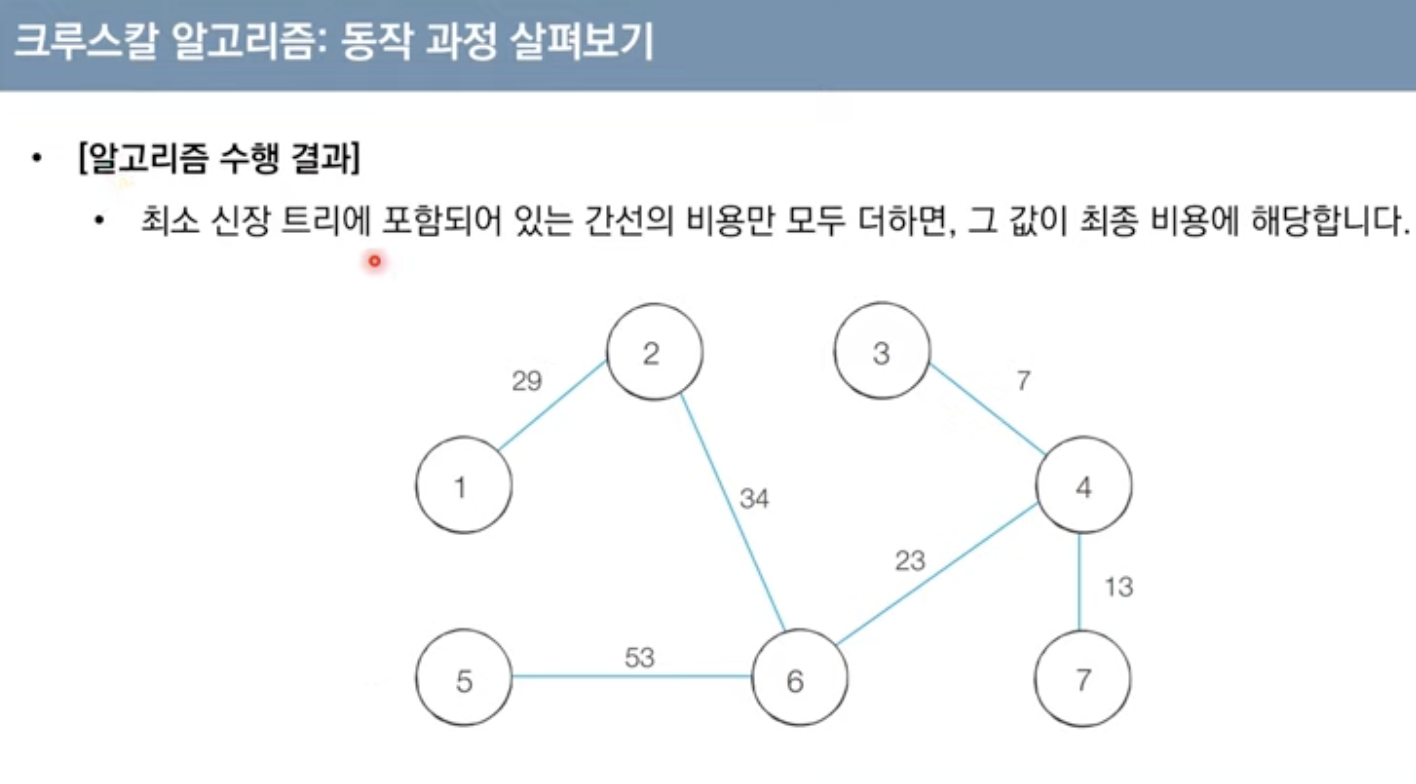
최소 신장 트리
최소한의 비용으로 구성되는 신장 트리를 찾아야할때 어떻게 해야 할까
예를 들어 N개의 도시가 존재하는 상황에서 두 도시 사이에 도로를 놓아 전체 도시가 서로 연결 될 수 있개 도로를 설치하는 경우를 생각해볼떼-> 두 도시 A,B를 선택했을 때 A에서 B로 이동하는 경로가 반드시 존재하도록

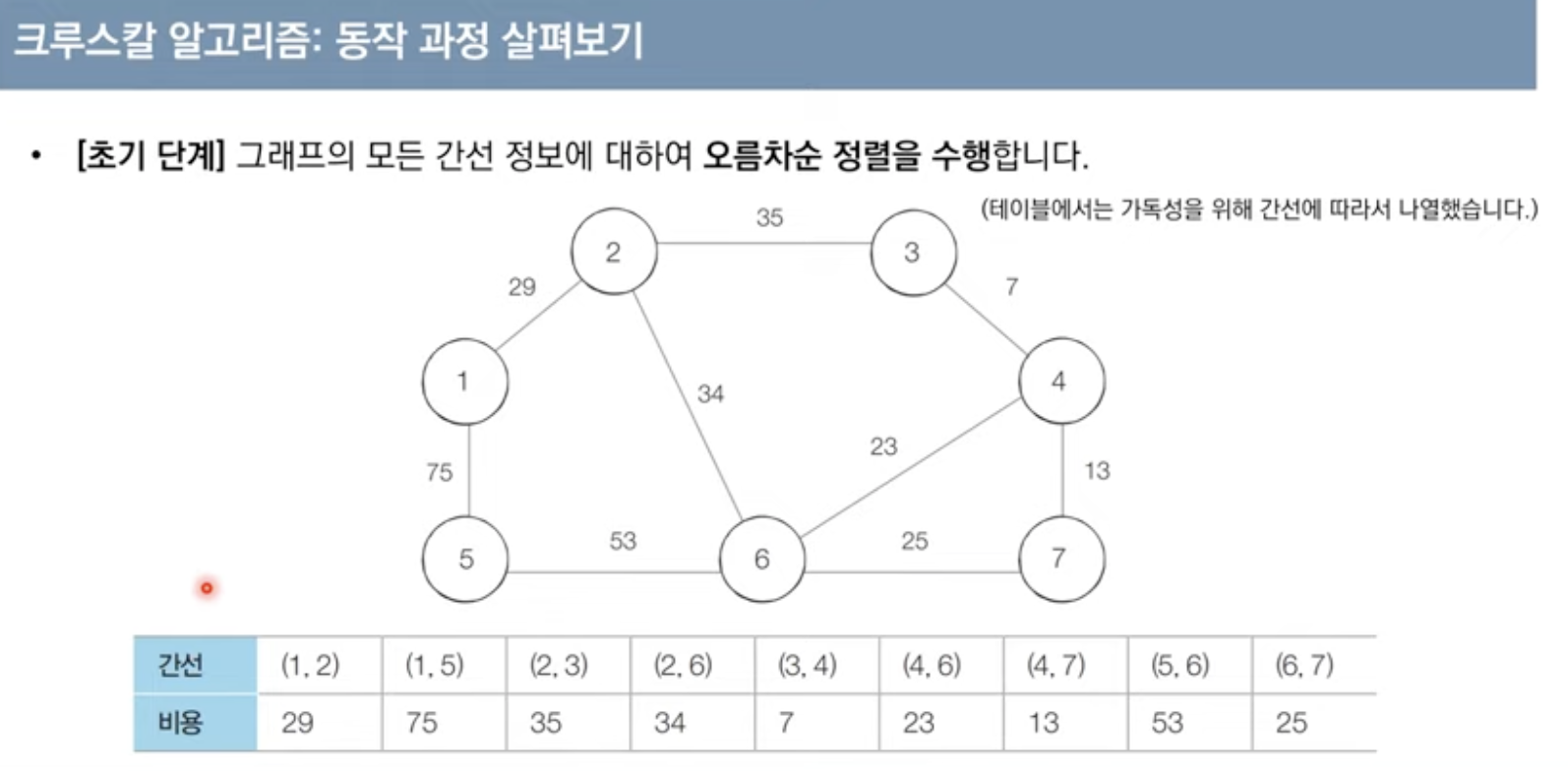
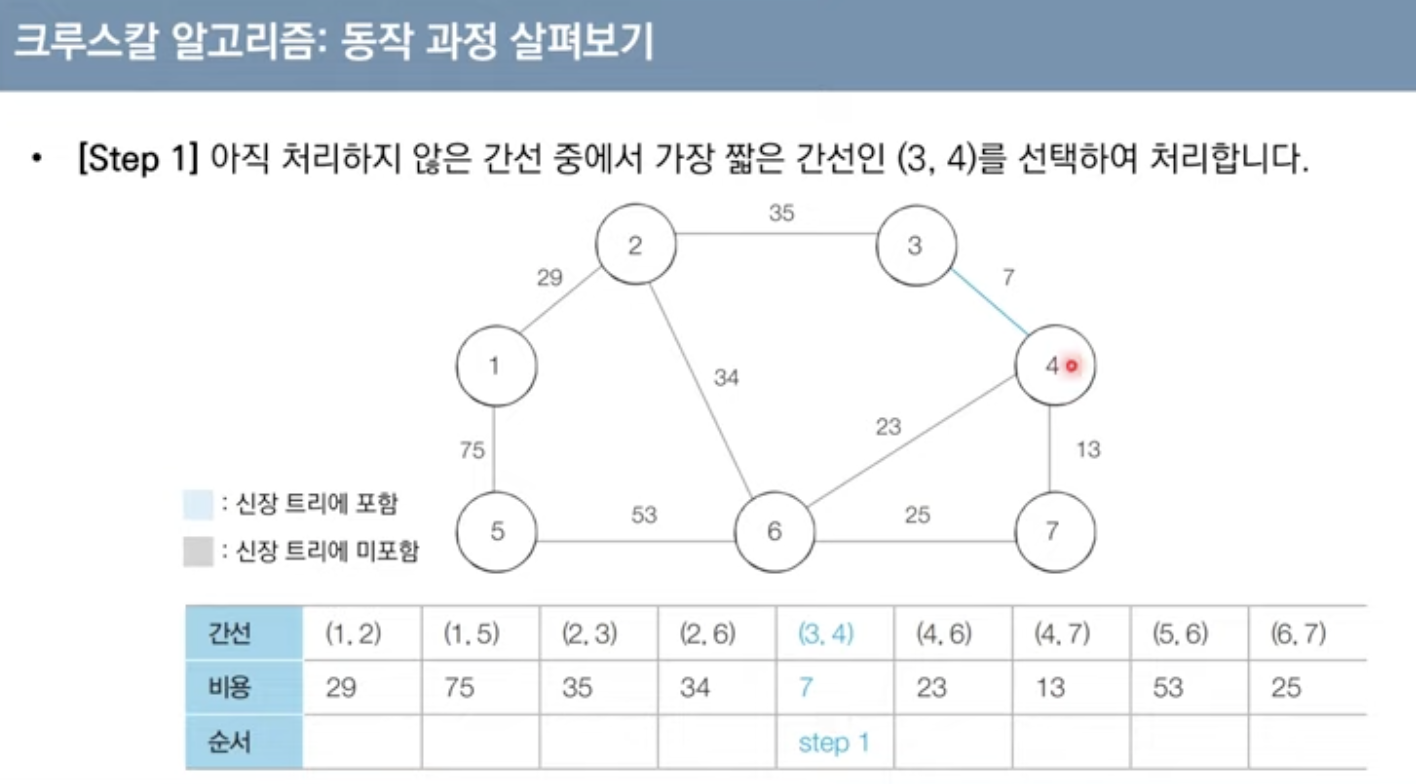
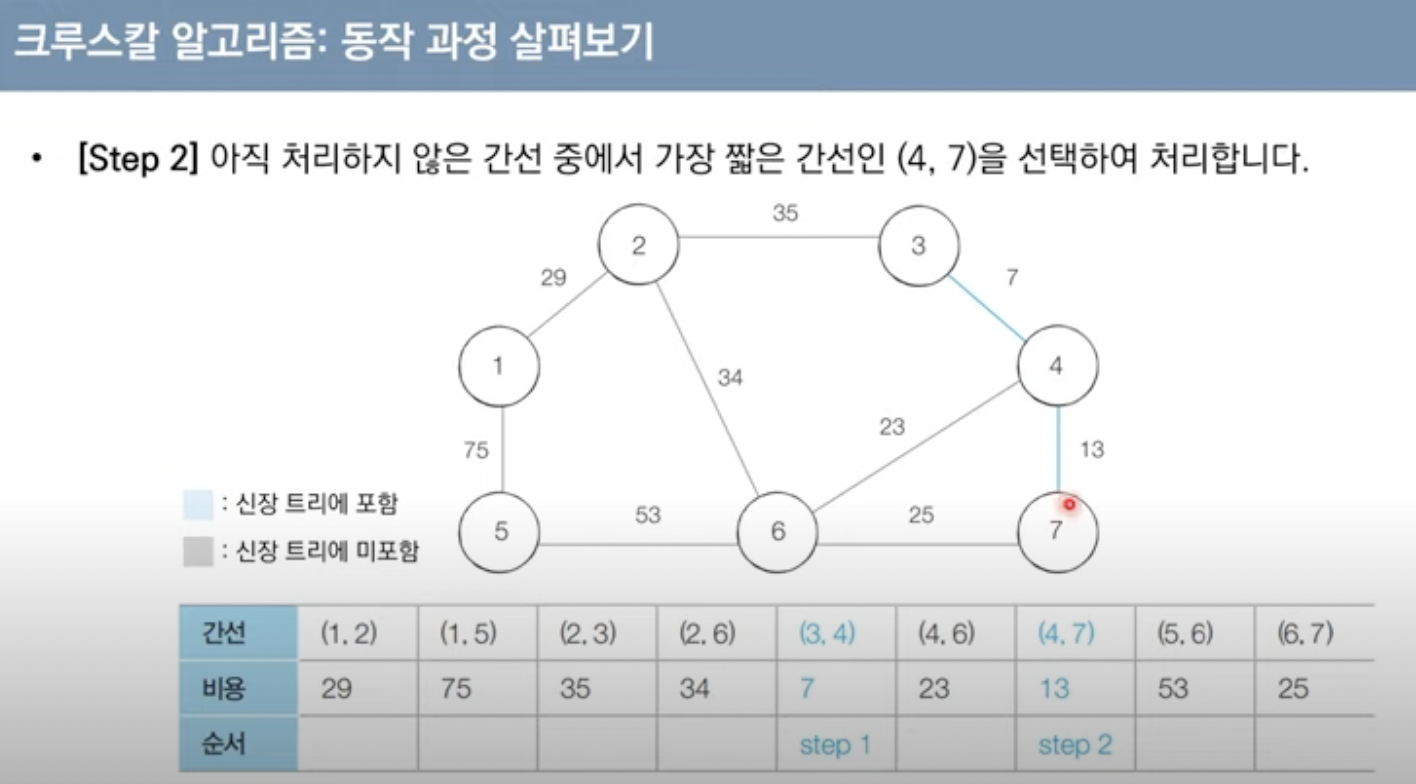
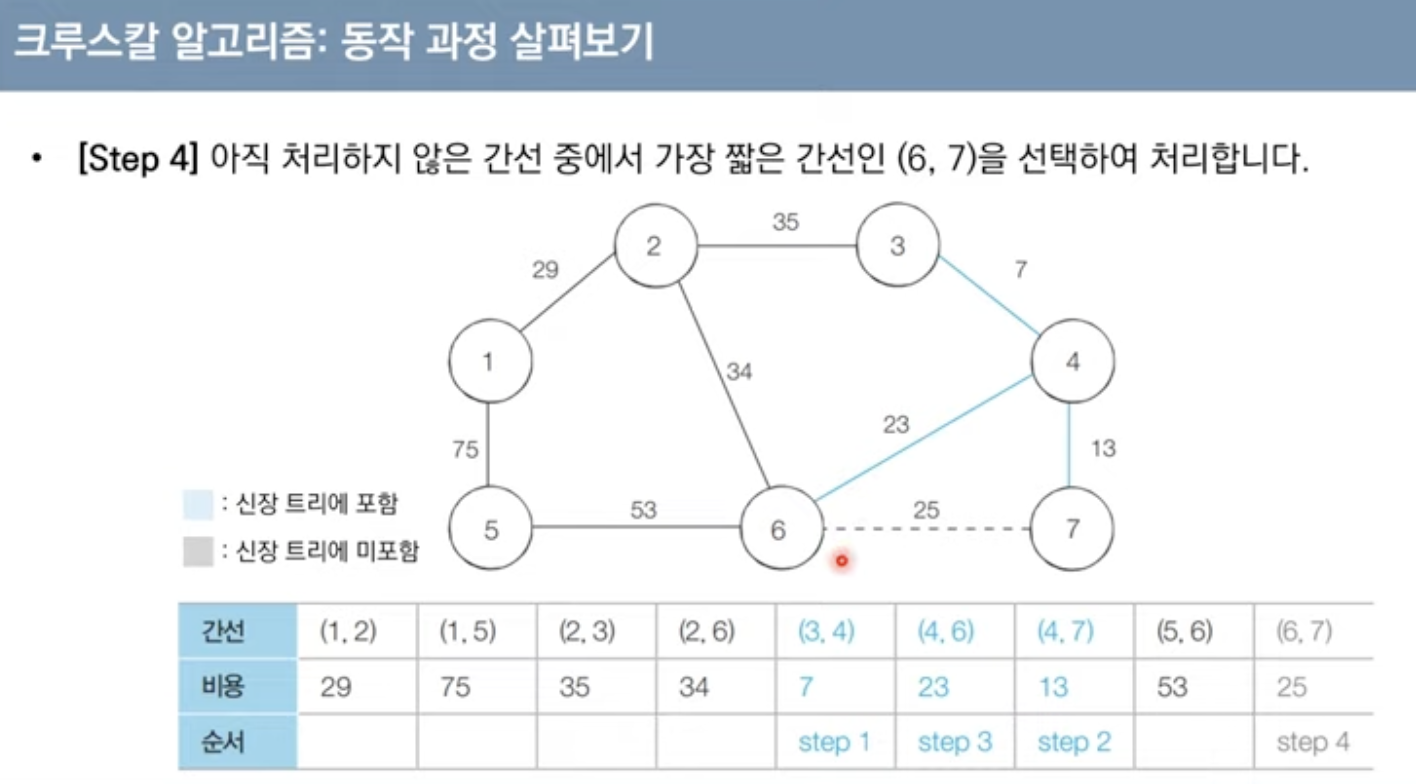
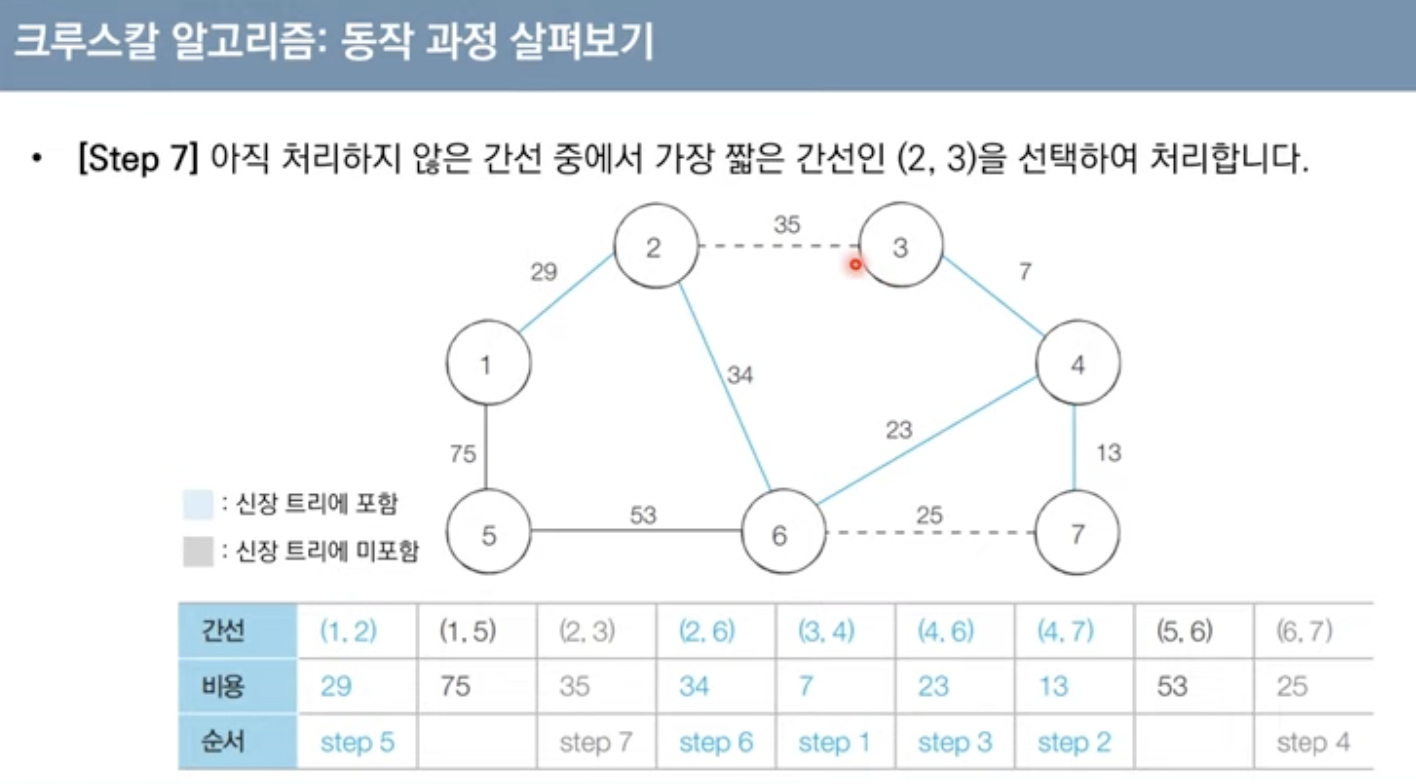
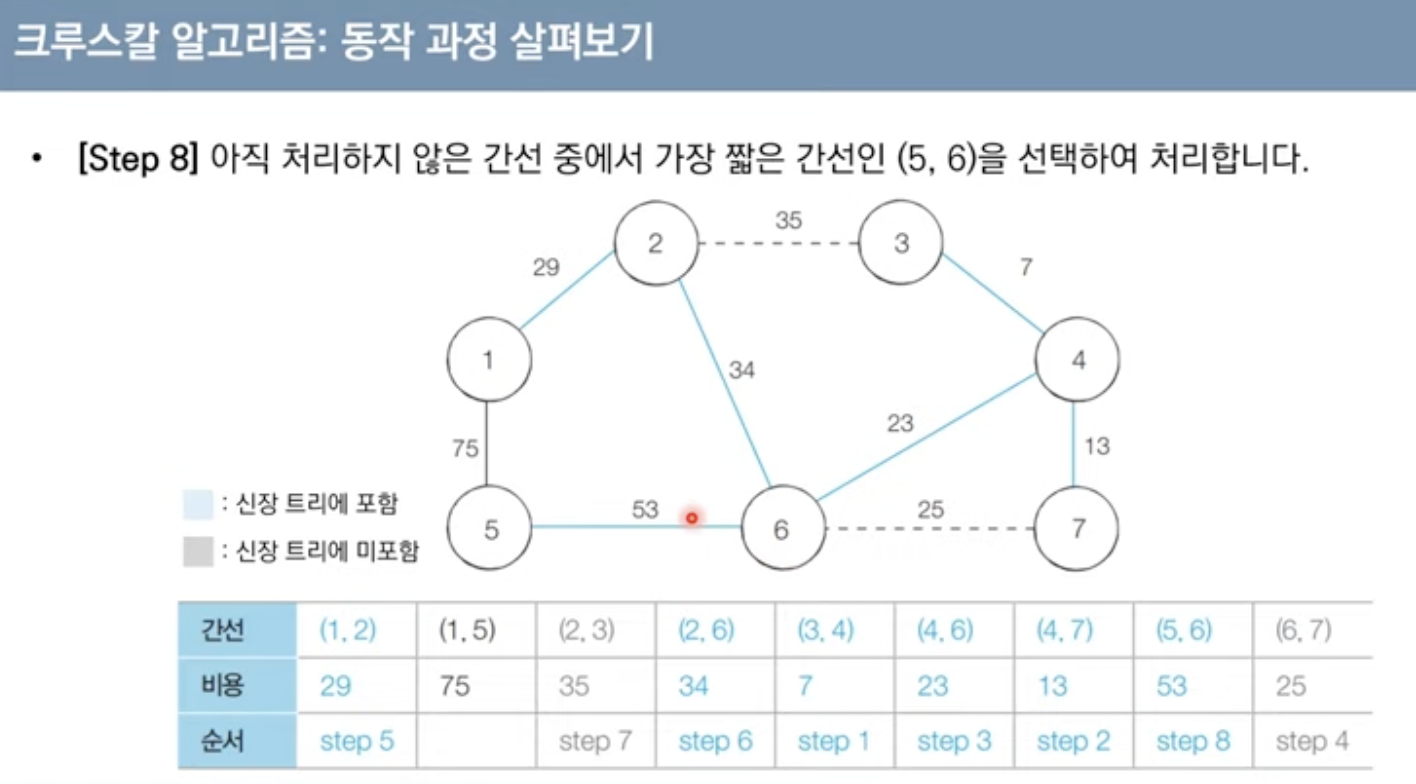
크루스칼 알고리즘
대표적인 최소 신장 트리 알고리즘(그리디 알고리즘)
구체적 동작
-간선 데이터를 비용에 따라 오름차순으로 정렬
-간선을 하나씩 확인하며 현재의 간선이 사이클을 발생시키는지 확인
1.사이클이 발생하지 않는 경우 최소. 신장트리에 포함



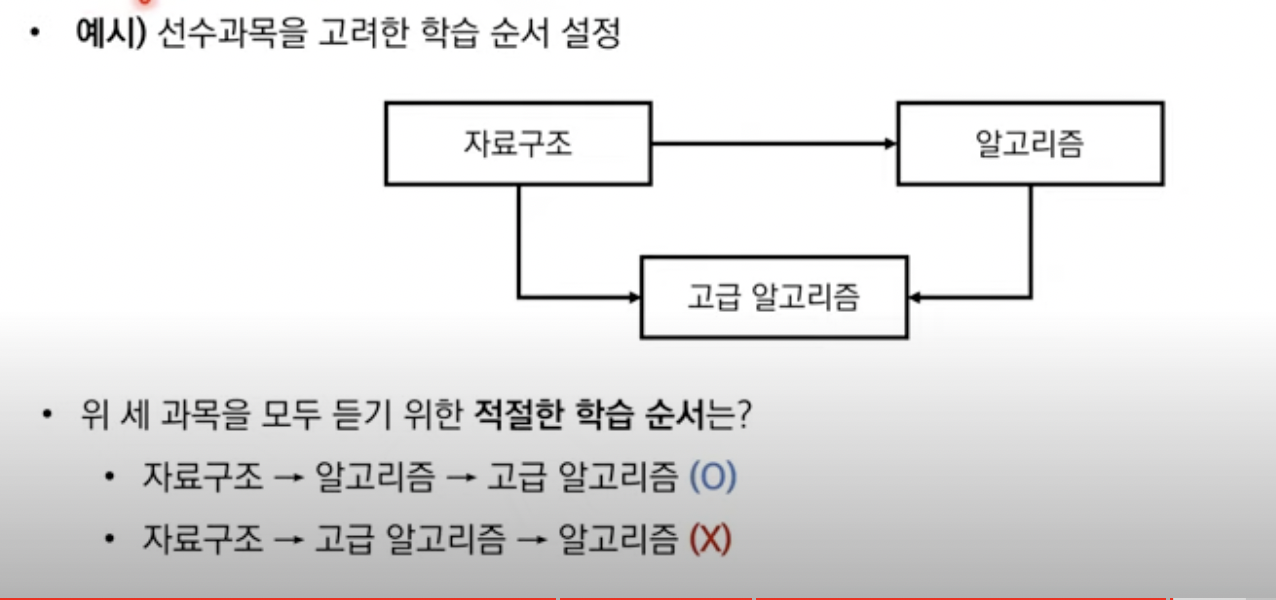
위상 정렬
사이클이 없는 방향 그래프의 모든 노드를 방향성에 거스르지 않도록 순서대로 나열하는 것
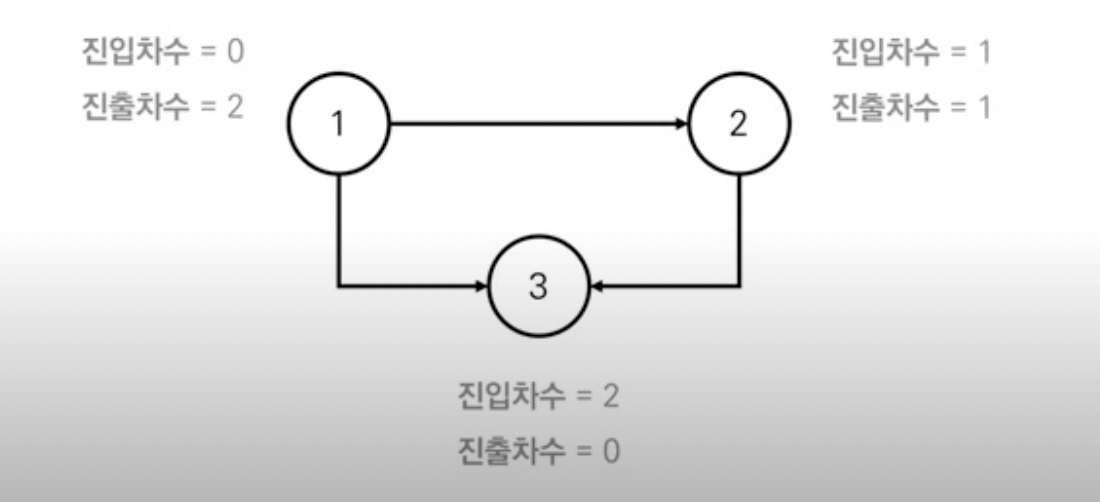
진입차수와 진출차수
진입차수: 특정한 노드로 들어오는 간선의 개수
진출차수: 특정한 노드에서 나가는 간선의 개수
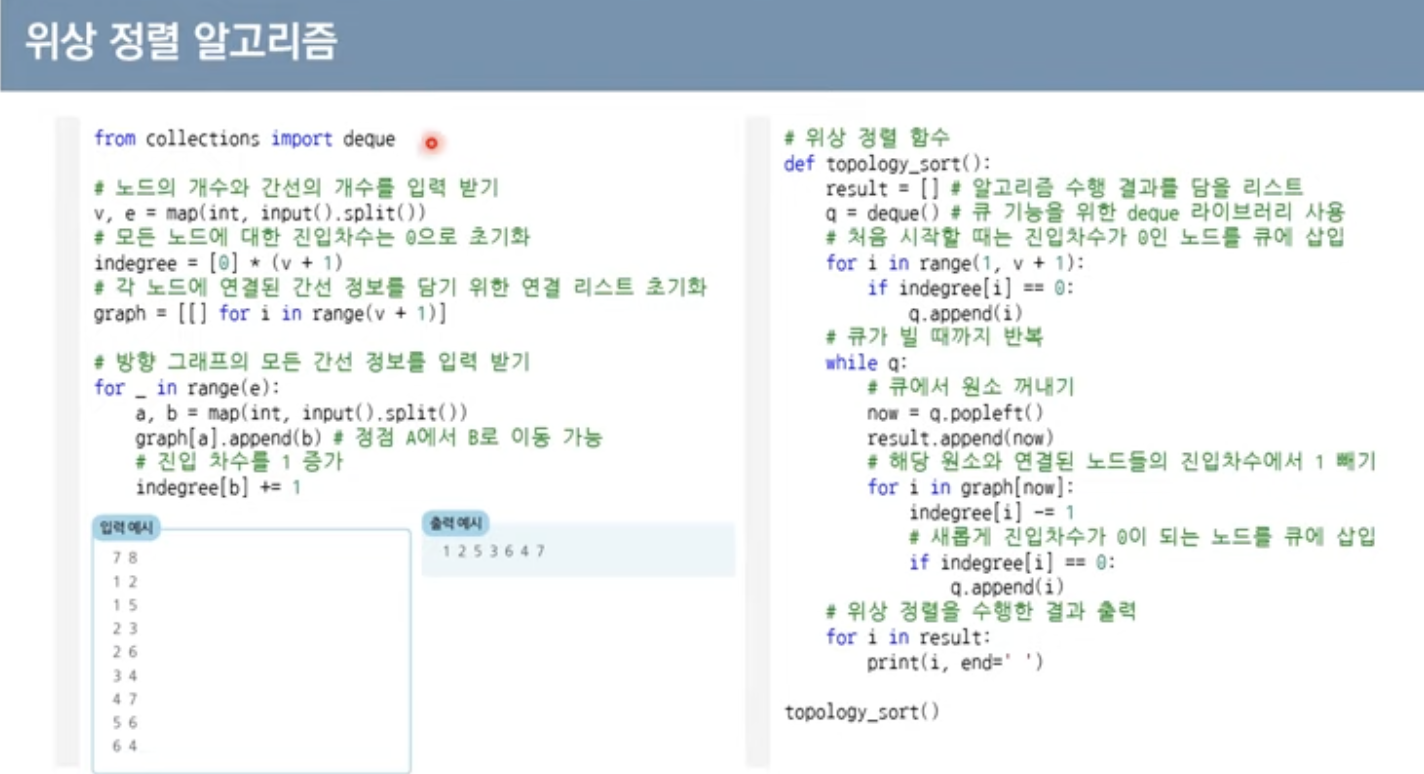
위상 정렬 알고리즘
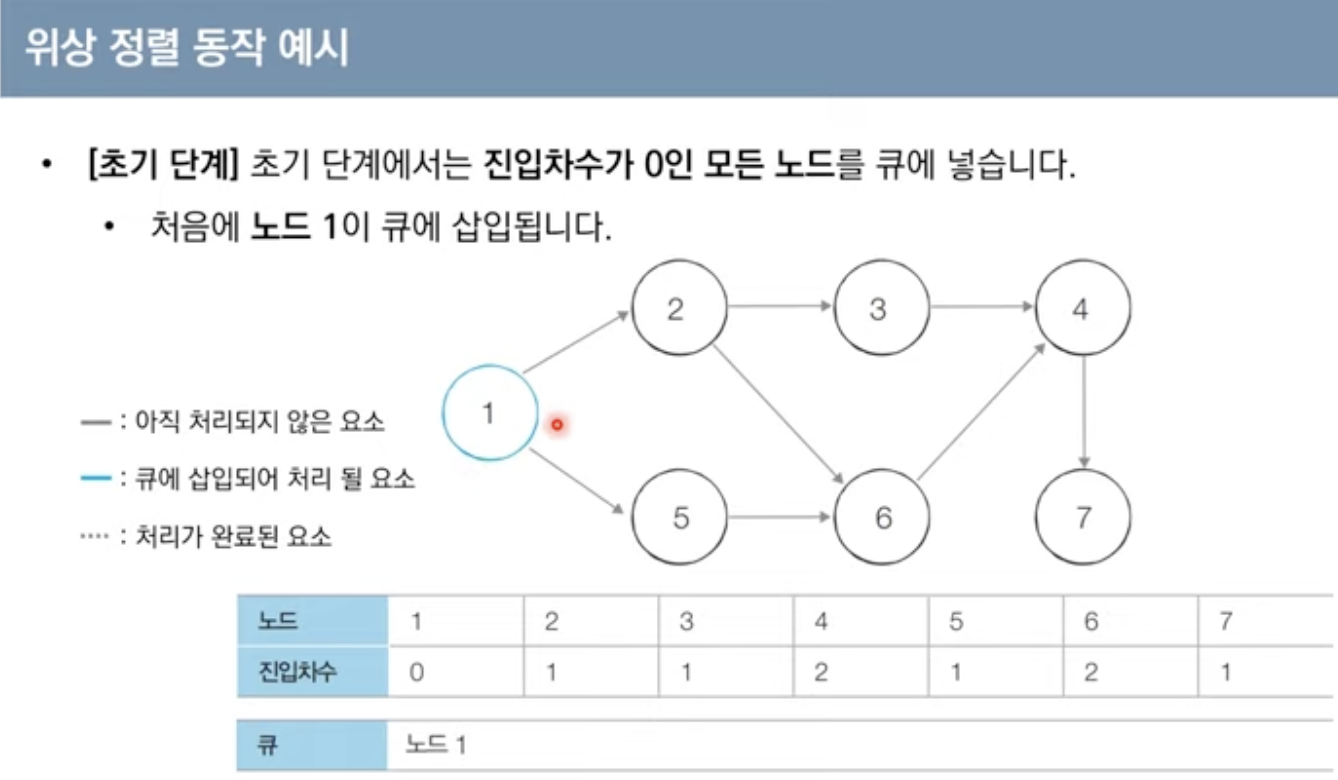
큐를 이용하는 위상 정렬 알고리즘의 동작과정
1.진입차수가 0인 모든 노드를 큐에 넣는다
2.큐가 빌때까지의 과정 반복
-큐에서 원소를 꺼내 해당 노드에서 나가는 간선을 그래프에서 제거
-새롭게 진입차수가 0이 된 노드를 큐에 넣기
-> 결과적으로 각 노드가 큐에 들어온 순서가 위상 정렬을 수행한 결과와 같음
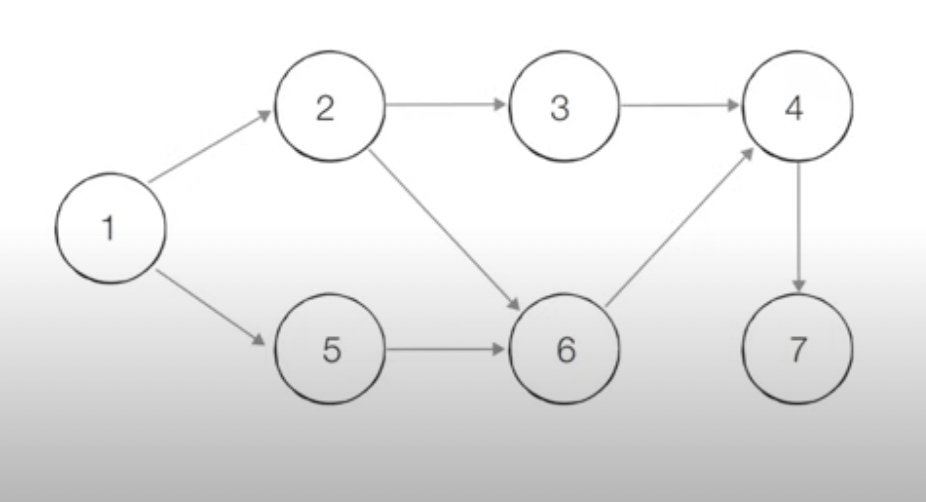
위상 정렬 동작 예시
위상 정렬을 수행할 그래프를 준비
-이때 그래프는 사이클이 없는 방향 그래프이어야 함

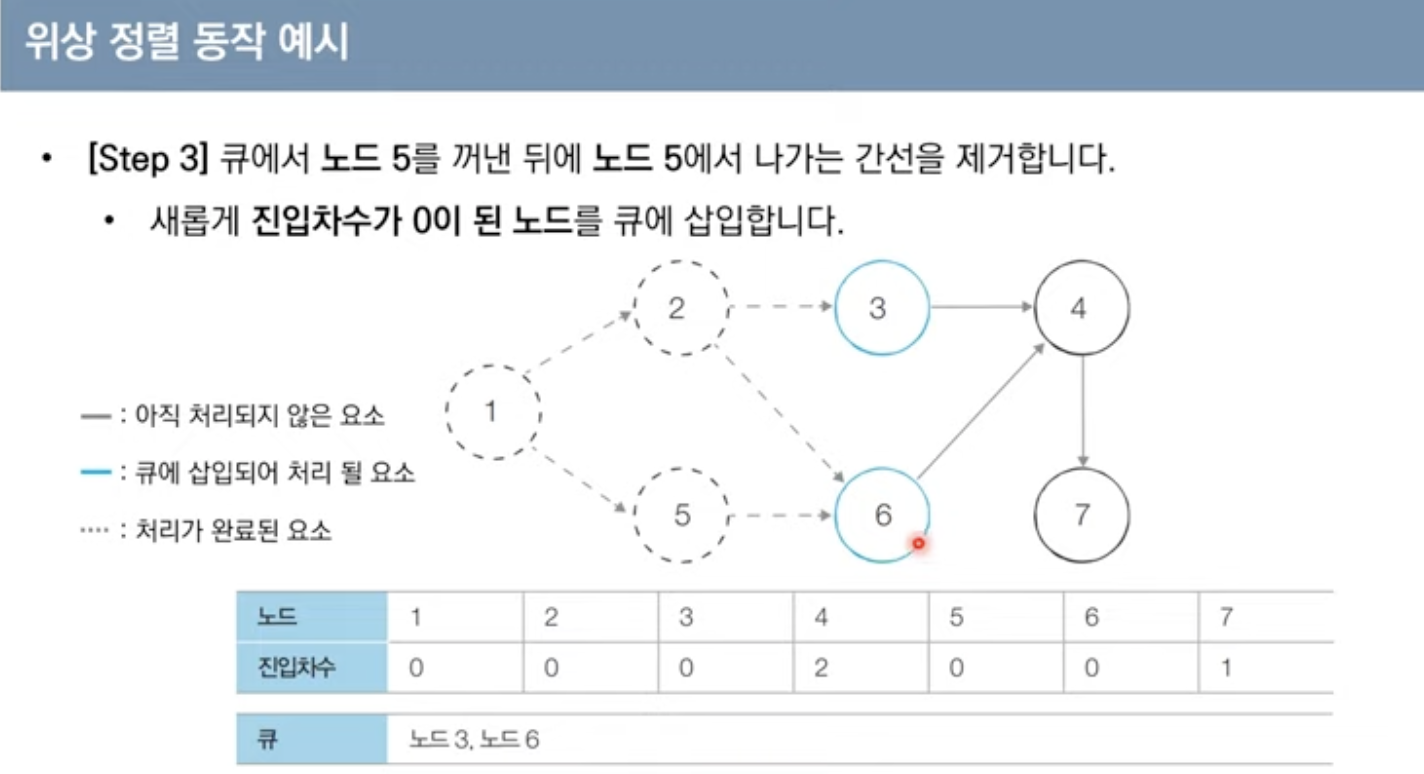
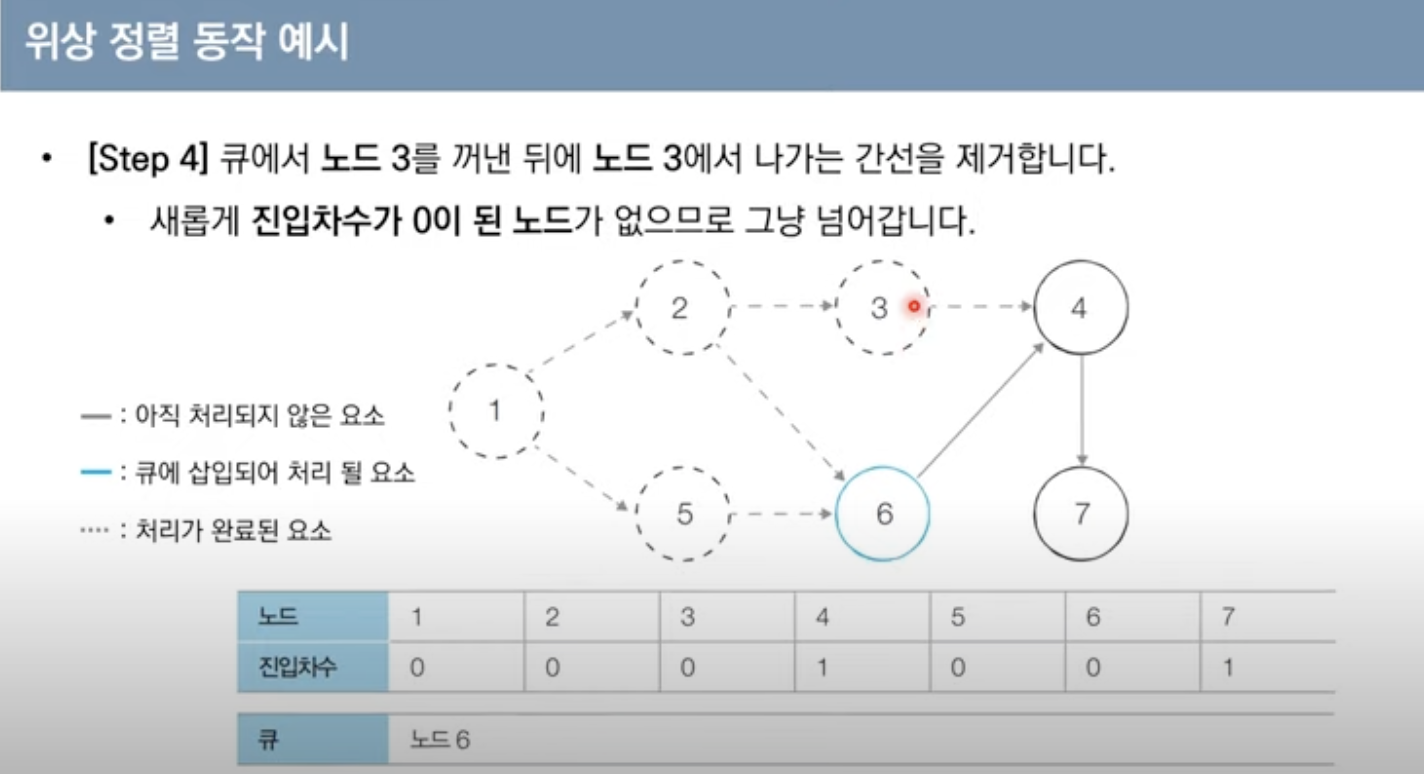




위상 정렬의 특징
1.위상정렬은 DAG에 대해서만 수행할 수 있다.
-DAG:순환하지 않는 방향 그래프
2.위상 정렬에서는 여러가지 답이 존재할 수 있다
-한 단계에서 큐에 새롭게 들어가는 원소가 2개 이상인 경우 여러가지 답 존재
3.모든 원소를 방문하기 전에 큐가 비면 사이클 존재한다고 판단
-사이클에 포함된 원소 중에서 어떠한 원소도 큐에 들어가지 못함
4.스택을 이용한 dfs를 이용해 위상 정렬을 수행할 수 있음