8W1D-기타 그래프 이론

기타 그래프 이론

서로소 집합

:공통원소가 없는 두 집합을 의미.
서로소 부분 집합들로 나누어진 원소들의 데이터를 처리하기 위한 자료구조

서로소 집합 자료구조는 두 종류의 연산을 지원
1.합집합: 두개의 원소가 포함된 집합을 하나의 집합으로 합치는 연산
2.찾기: 특정한 원소가 속한 집합이 어떤 집합인지 알려주는 연산
(서로소 집합 자료구조는 합치기 찾기 자료구조라고 불리기도 함)

여러개의 합치기 연산이 주어졌을 때
1. 합집합연산을 확인하여, 서로 연결된 두 노드 a,b를 확인
-a,b의 루트 노드 a',b'를 각각 찾기
-a',b'의 부모 노드로 설정
2.모든 합집합연산을 처리할때까지 1번의 과정을 반복

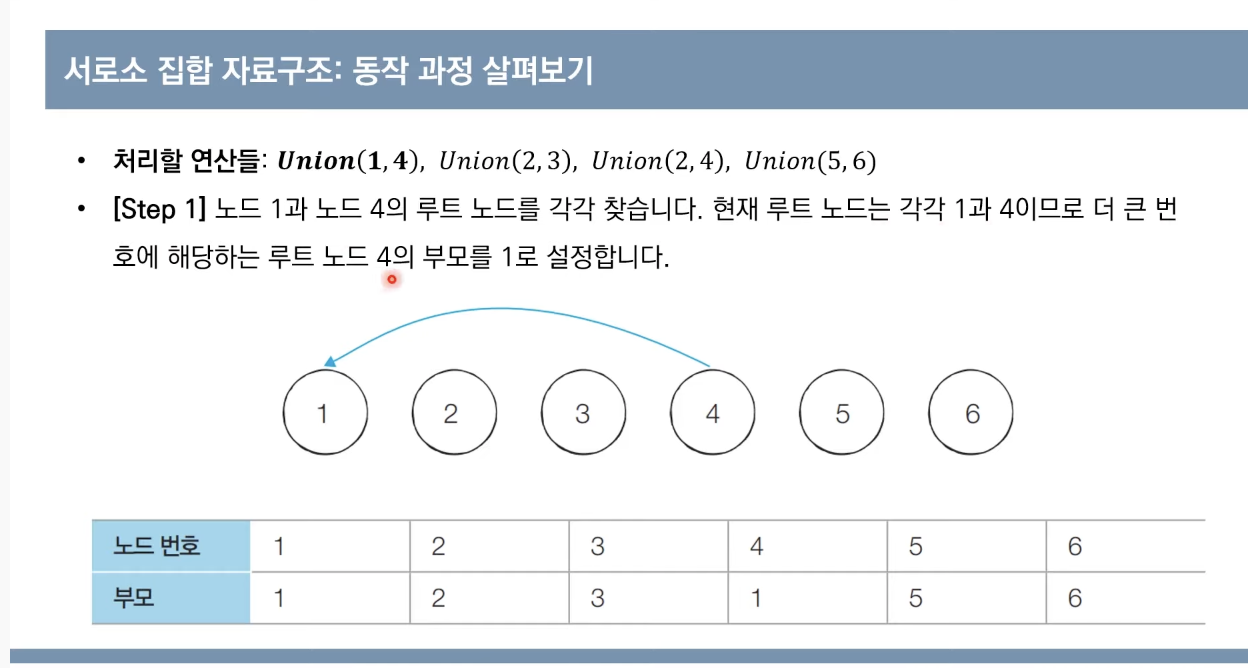
노드4,부모4->노드4,부모1
여섯개의 각각의 집합
노드3,부모3->노드3,부모2
노드2,부모2->노드2,부모1

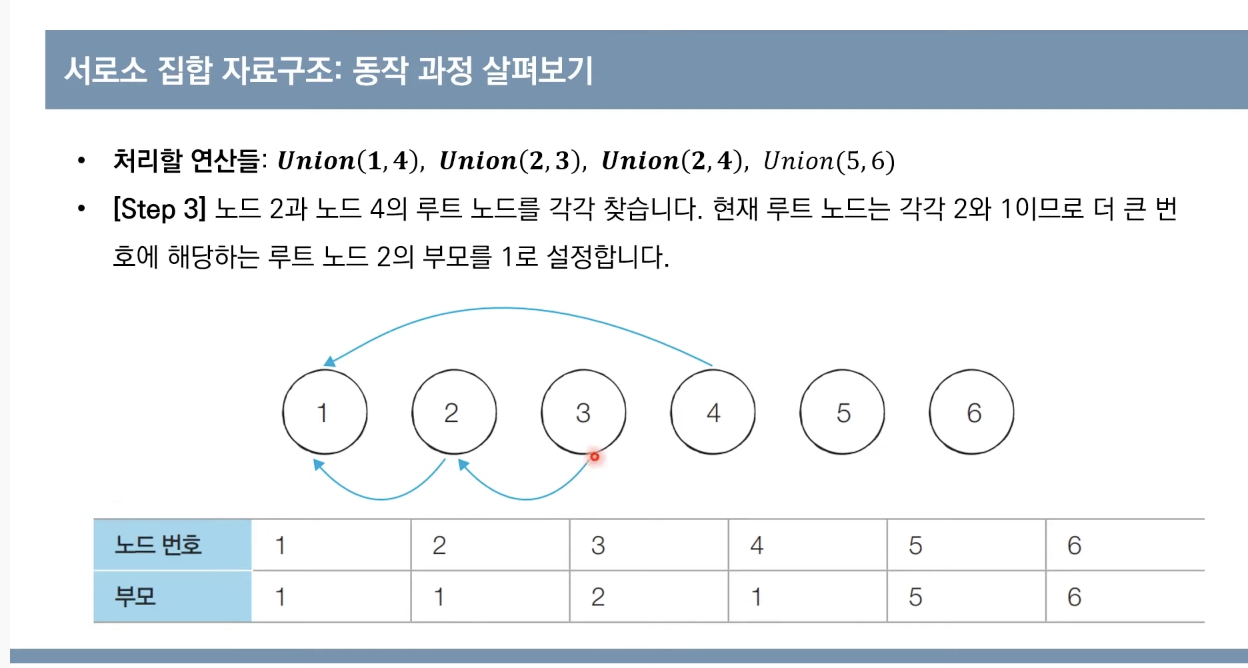
노드6,부모6->노드6,부모5

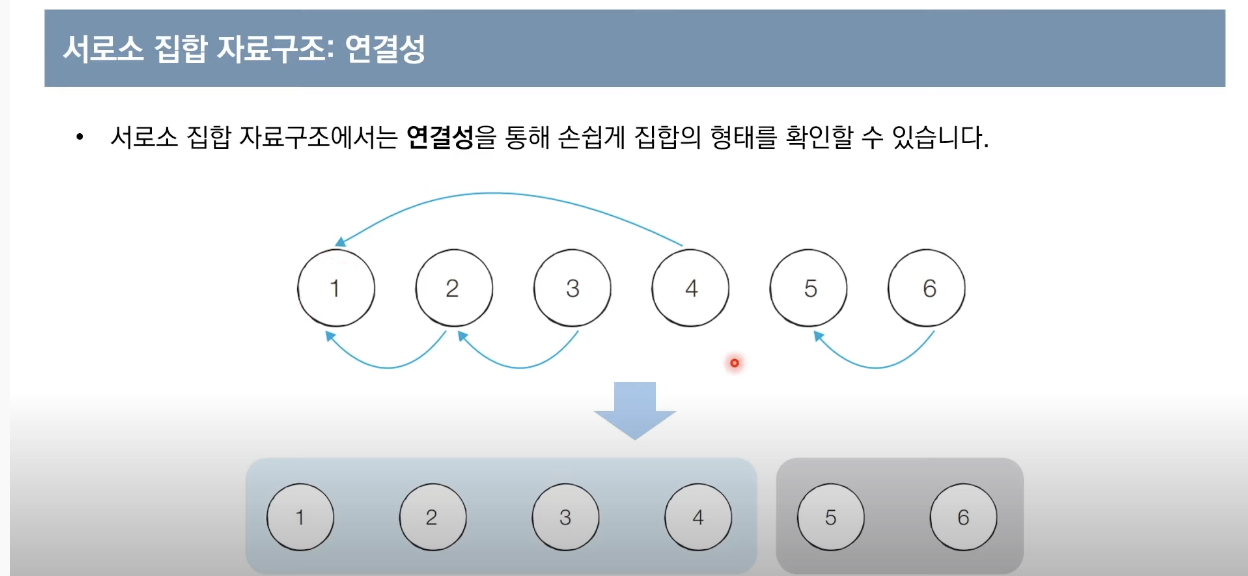
서로소 집합 자료구조:연결성

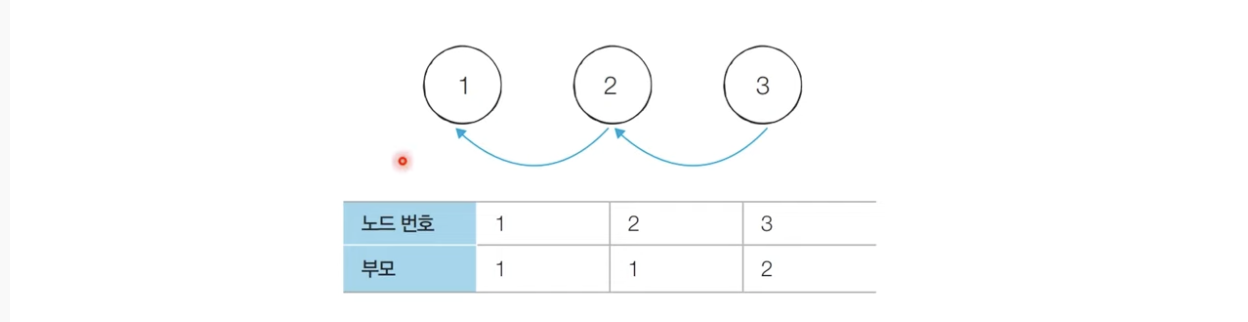
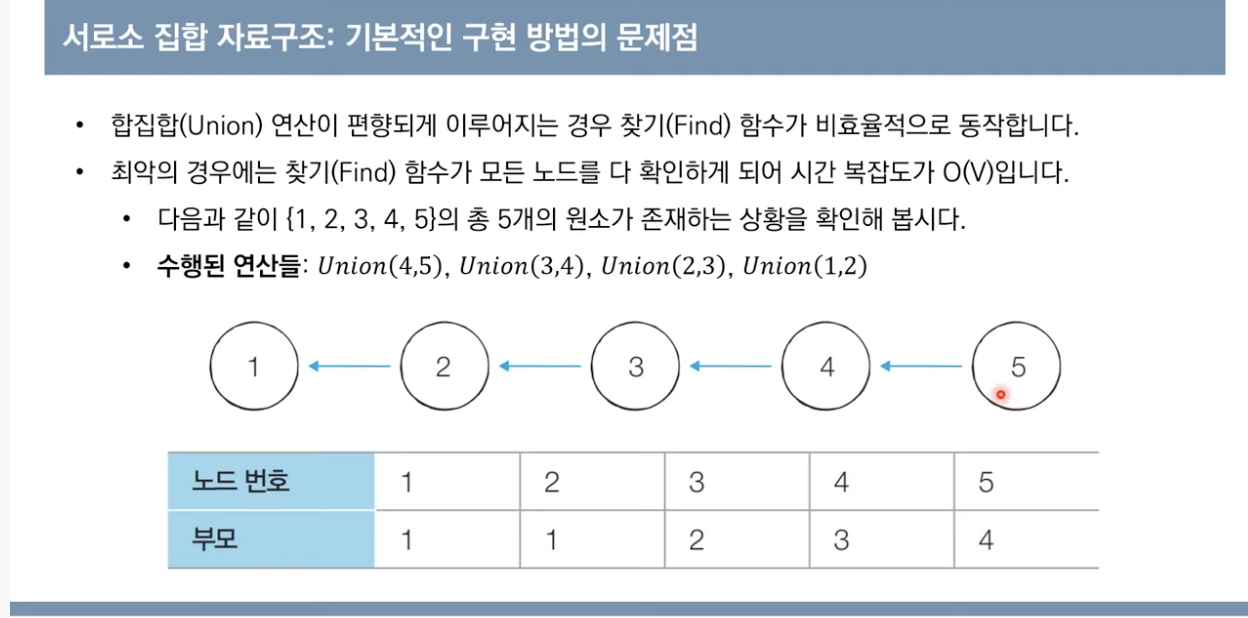
-기본적인 형태의 서로소 집합 자료구조에서는 루트 노드에 즉시 접근할 수 없음
-루트노드를 찾기 위해 부모 테이블을 계속해서 확인하며 거슬러 올라가야함
-다음예시에서 노드3의 루트를 찾기위해서는 노드2를 거쳐 노드1에 접근해야함

서로소 집합 자료구조:경로 압축

찾기 함수를 최적화 하기 위한 방법으로 경로 압축을 이용할 수 있다
찾기 함수를 재귀적으로 호출한 뒤에 부모 테이블 값을 바로 갱신.

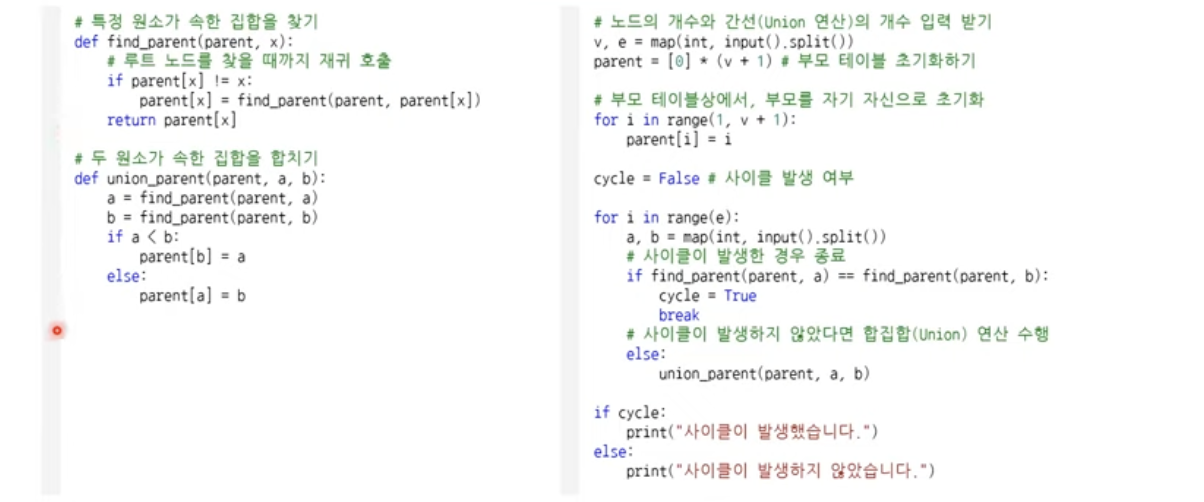
#특정 원소가 속한 집합을 찾기
def find_parent(parent,x):
	#루트 노드가 아니라면 루트 노드를 찾을 때까지 재귀적으로 호출 
    if parent[x] !=x
    	parent[x]=find_parent(parent,parent[x])
    return parent[x]
    

서로소 집합 자료구조: 경로압축

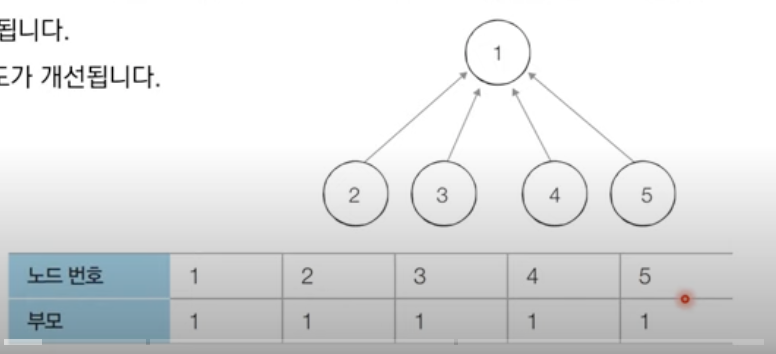
-경로압축 기법을 적용하면 각 노드에 대해 찾기함수를 호출한 이후에 해당노드의 루트노드가 바로 부모노드가 됨.
-동일한 예시에 대해 모든 합집합함수를 처리한 후 각 원소에 대해 찾기 함수를 수행하면 다음과 같이 부모 테이블이 갱신됨
-기본적인 방법에 비해 시간 복잡도가 개선됨

서로소 집합을 활용한 사이클 판별

서로소 집합은 무방향 그래프 내에서의 사이클을 판별할때 사용
-방향 그래프에서의 사이클 여부는 dfs를 이용하여 판별
사이클 판별 알고리즘
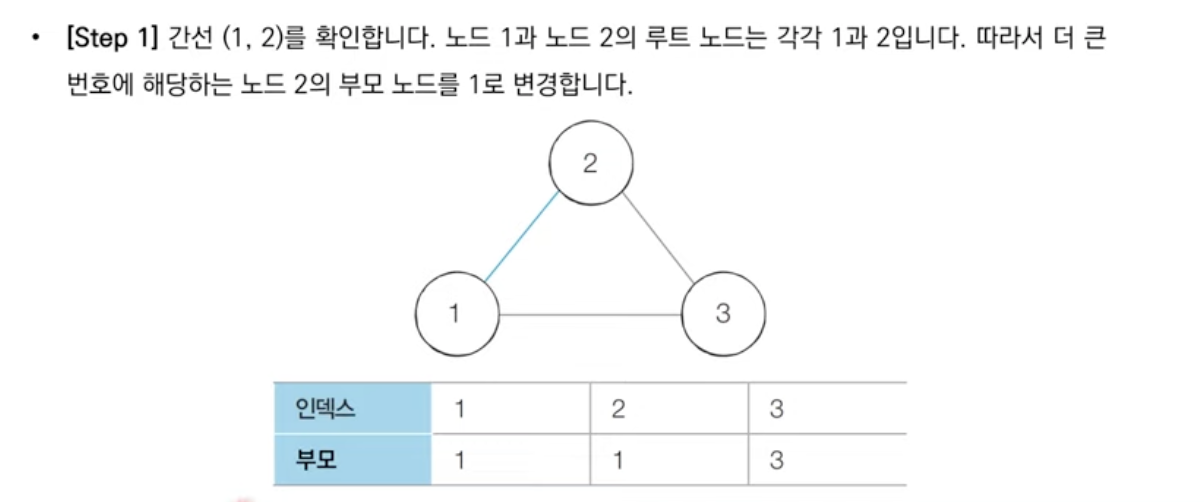
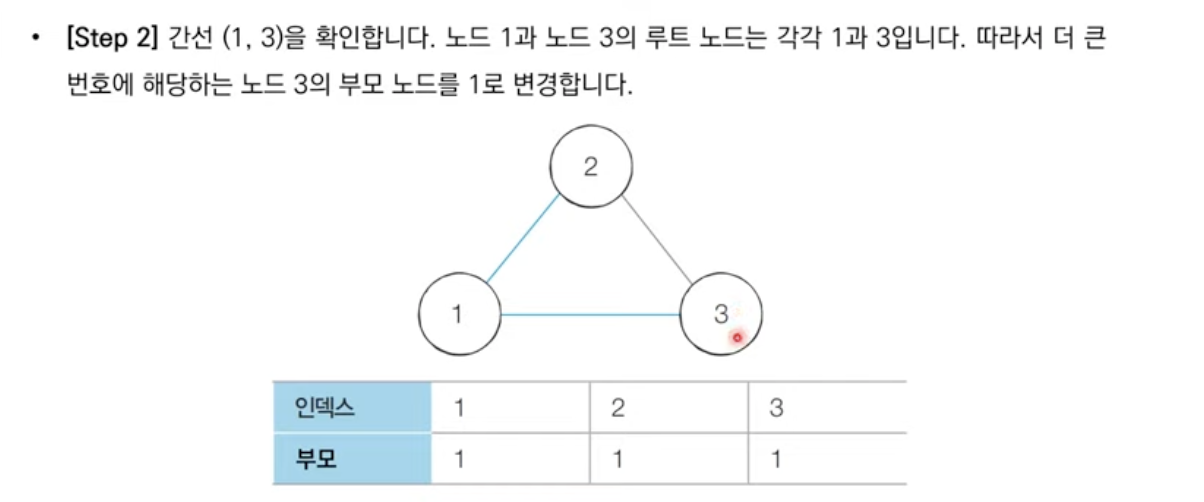
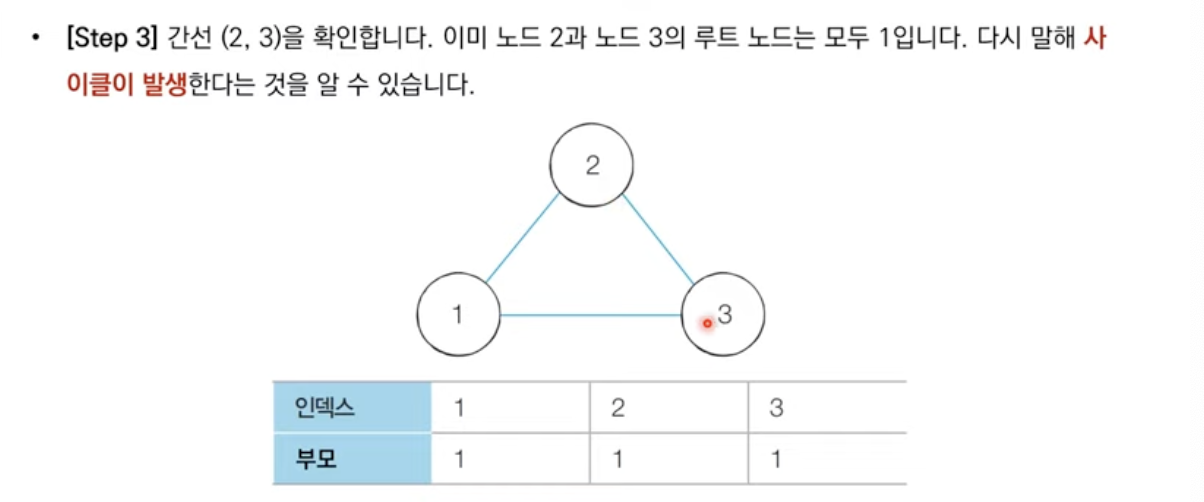
1.각 간선을 하나씩 확인하면서 두 노드의 루트 노드를 확인
-루트 노드가 서로 다르면 두 노드에 대해 합집합 연산을 수행
-루트 노드가 서로 같으면 사이클이 발생한 것
2.그래프에 포함되어 있는 모든 간선에 대해 1번과정 반복

서로소 집합을 활용한 사이클 판별: 동작 과정 살펴보기