컴퓨터 과학에서 데이크스트라 알고리즘(영어: Dijkstra algorithm) 또는 다익스트라 알고리즘은 도로 교통망 같은 곳에서 나타날 수 있는 그래프에서 꼭짓점 간의 최단 경로를 찾는 알고리즘이다. 이 알고리즘은 컴퓨터 과학자 에츠허르 데이크스트라가 1956년에 고안했으며 삼 년 뒤에 발표했다.
--위키피디아 피셜
다익스트라가 무엇인고 하니
최단경로끼리 막 더하고 볶고 지지고 해서 가장 짧은걸로 해줌
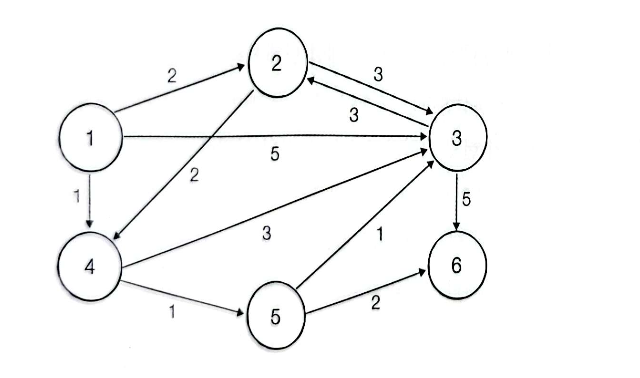
이 그림으로 이해해보자
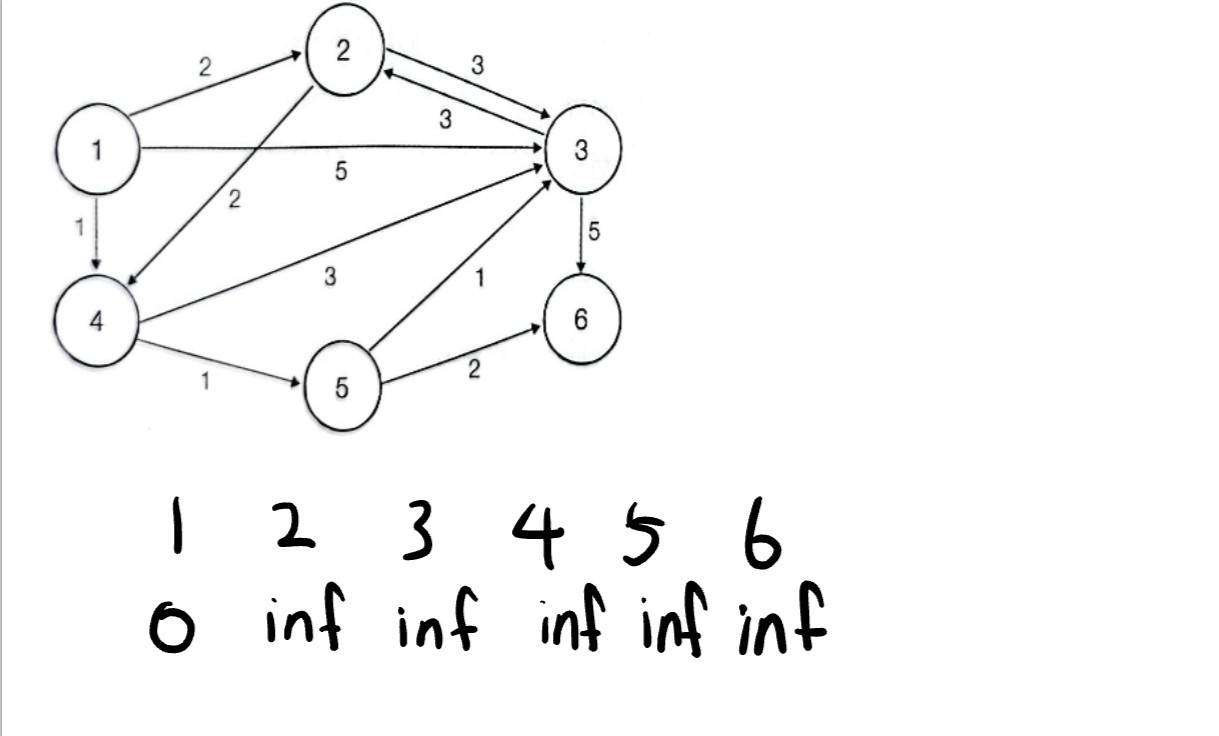
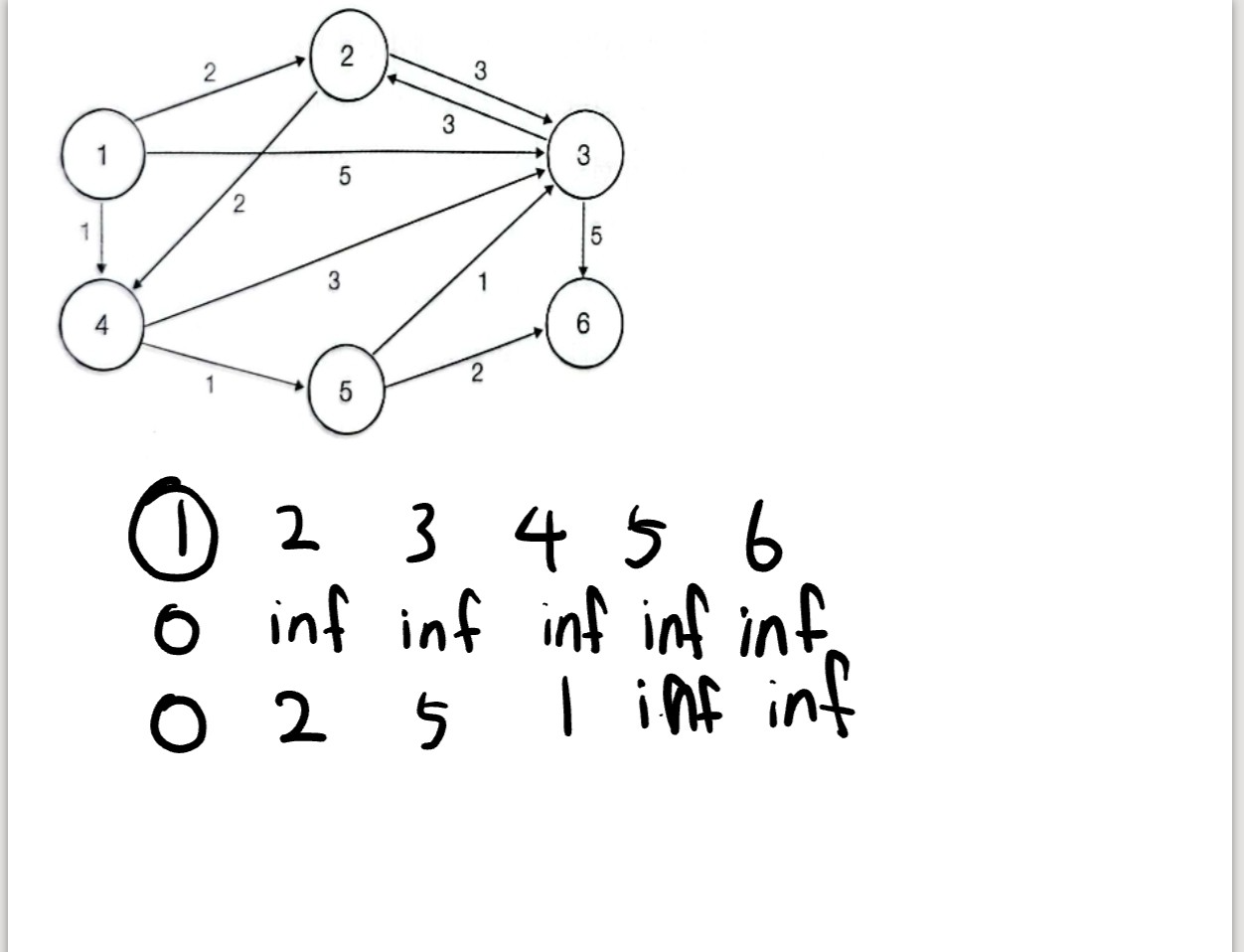
1번 노드만 거칠때 갈수있는곳
그리고 가장 작은 값으로 가줌
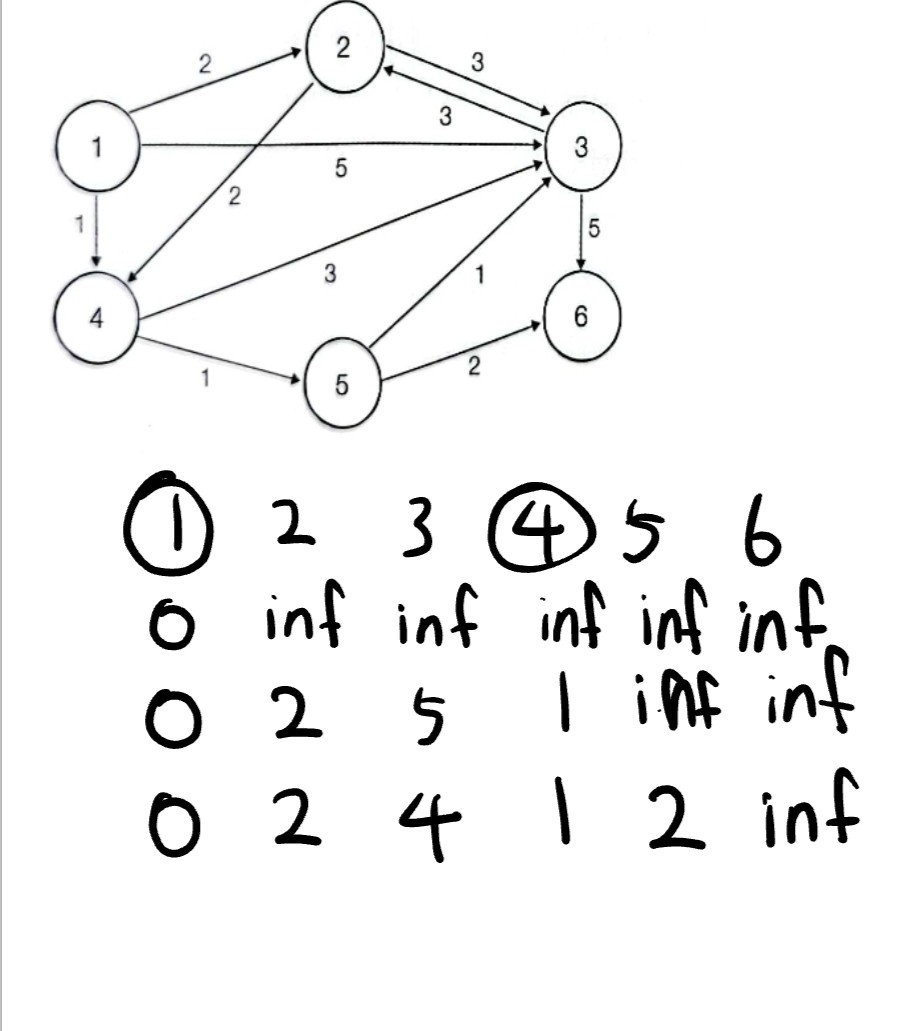
4번 노드를 거치고 가는거랑 안거치고 가는거랑 비교해서 작은걸로 해줌.
그리고 가장작은 2번으로감
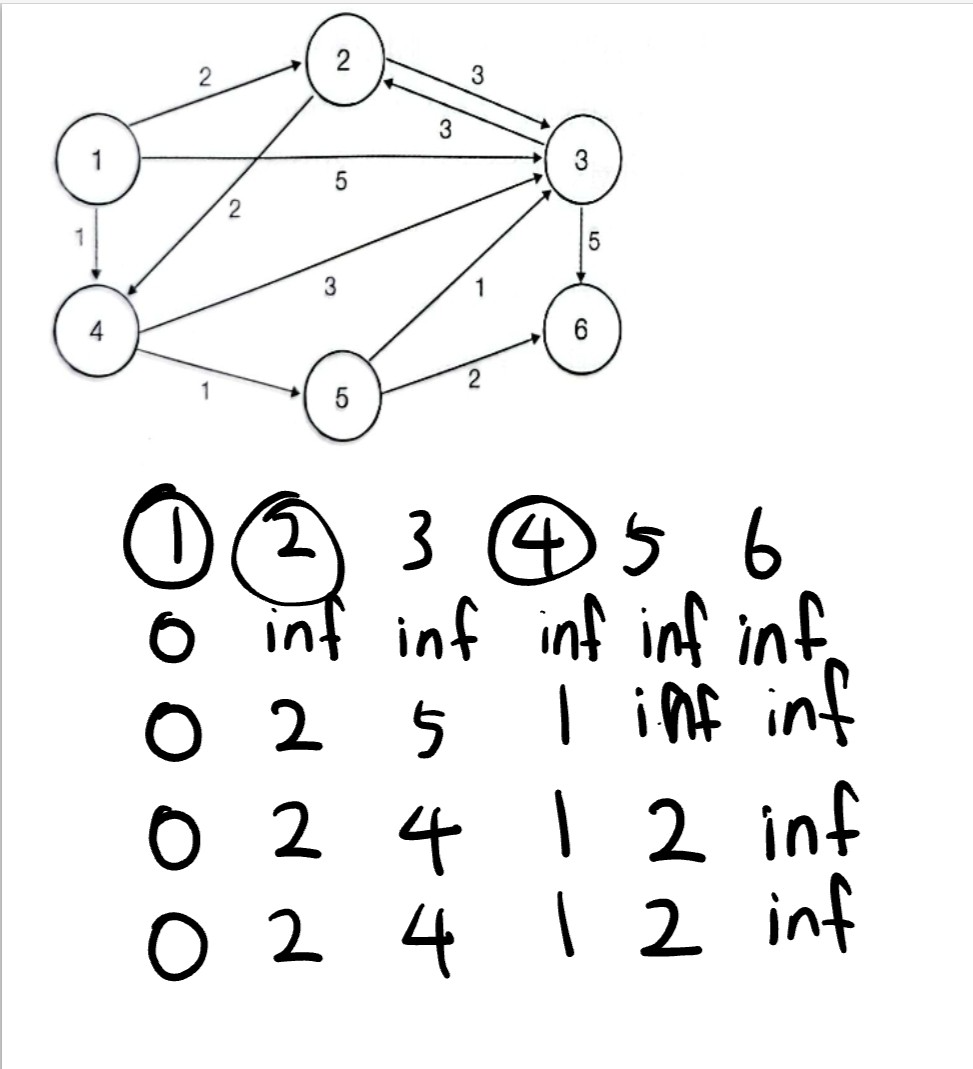
2번 노드를 거치고 가는거랑 안거치고 가는거랑 비교해서 작은걸로 해줌
그리고 가장작은 5번으로 가줌
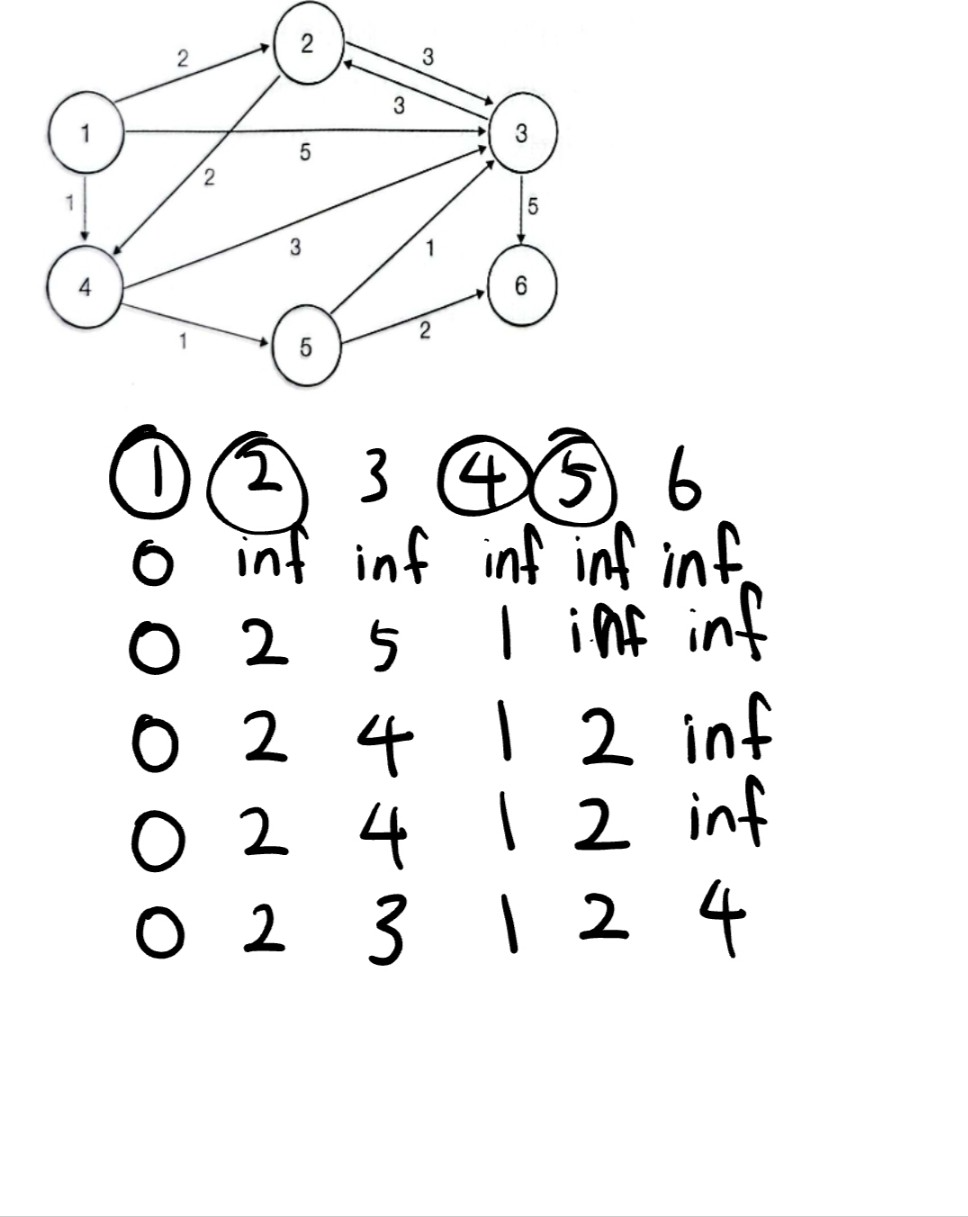
5번 노드를 거치고 가는거랑 안거치고 가는거랑 비교해서 작은걸로 해줌
그리고 가장작은 3번으로 가줌
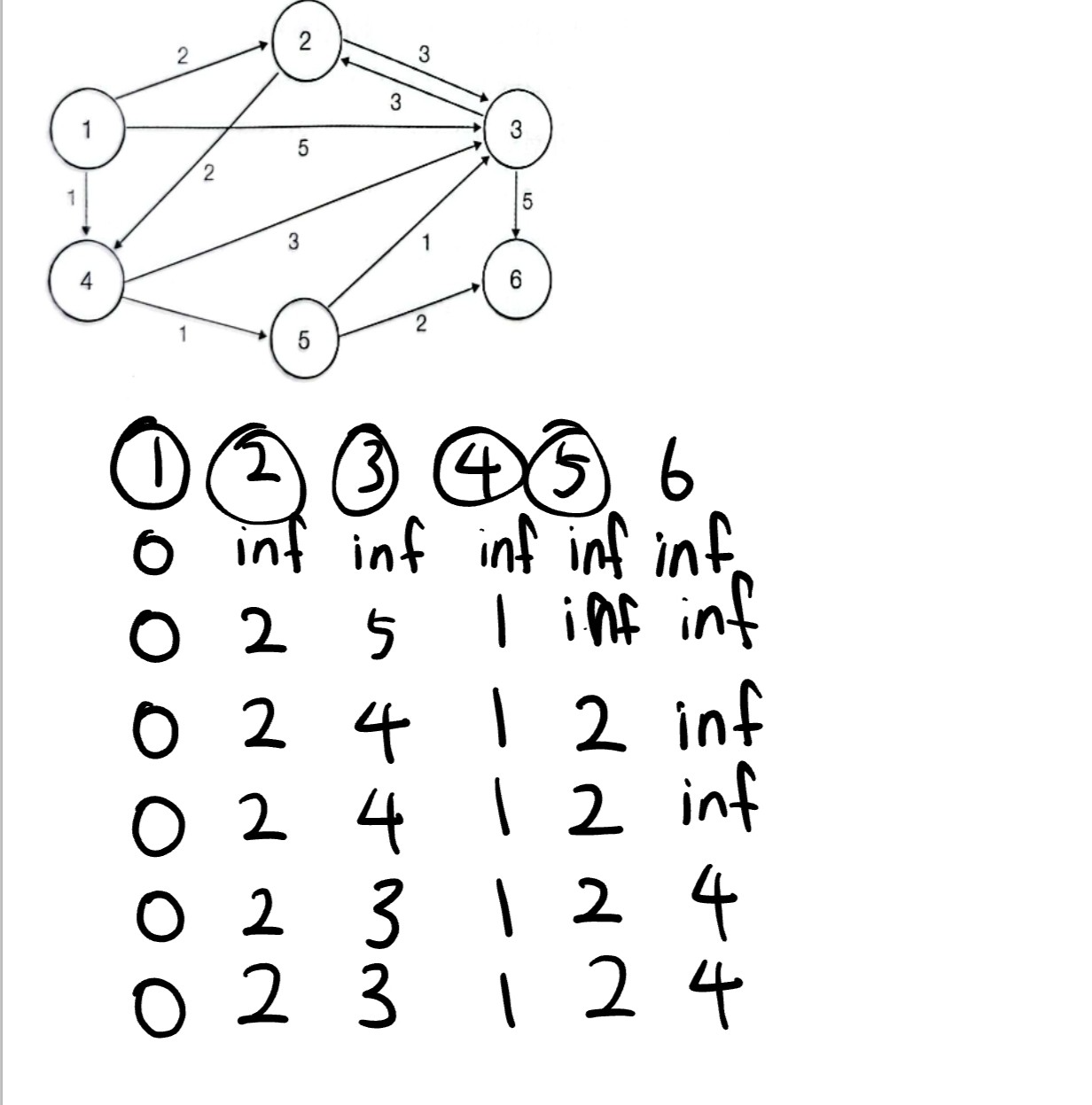
5번 노드를 거치고 가는거랑 안거치고 가는거랑 비교해서 작은걸로 해줌
그리고 끝이남 이쯤됐으면 감이 뽝 오죠??
import sys
input = sys.stdin.readline
INF = int(1e9)
n, m = map(int, input().split())
start = int(input())
graph = [[] for i in range(n + 1)]
visited = [False] * (n + 1)
distance = [INF] * (n + 1)
for _ in range(m):
a, b, c = map(int, input().split())
graph[a].append((b, c))
def get_smallest_node():
min_value = INF
index = 0
for i in range(1, n + 1):
if distance[i] < min_value and not visited[i]:
min_value = distance[i]
index = i
return index
def dijkstra(start):
distance[start] = 0
visited[start] = True
for j in graph[start]:
distance[j[0]] = j[1]
for i in range(n - 1):
now = get_smallest_node()
visited[now] = True
for j in graph[now]:
cost = distance[now] + j[1]
if cost < distance[j[0]]:
distance[j[0]] = cost
dijkstra(start)
for i in range(1, n + 1):
if distance[i] == INF:
print("INF")
else:
print(distance[i])이건 get_smallest_node()로 가장 작은 노드를 찾아줌
import heapq
import sys
input = sys.stdin.readline
INF = int(1e9)
n, m = map(int, input().split())
start = int(input())
graph = [[] for i in range(n + 1)]
distance = [INF] * (n + 1)
for _ in range(m):
a, b, c = map(int, input().split())
graph[a].append((b, c))
def dijkstra(start):
q = []
heapq.heappush(q, (0, start))
distance[start] = 0
while q:
dist, now = heapq.heappop(q)
if distance[now] < dist:
continue
for i in graph[now]:
cost = dist + i[1]
if cost < distance[i[0]]:
distance[i[0]] = cost
heapq.heappush(q, (cost, i[0]))
dijkstra(start)
for i in range(1, n + 1):
if distance[i] == INF:
print("INFINITY")
else:
print(distance[i])
이거는 우선순위 큐를 이용한거임
우선순위큐로 가장 거리가 짧은 노드를 찾아줌
저것들은 빼고 한번 생각을 해보자
visited이거는 방문했냐고
distance이거는 우리가 열심히 그렸던 그 아래 표이고
graph는 위의 예제에서는
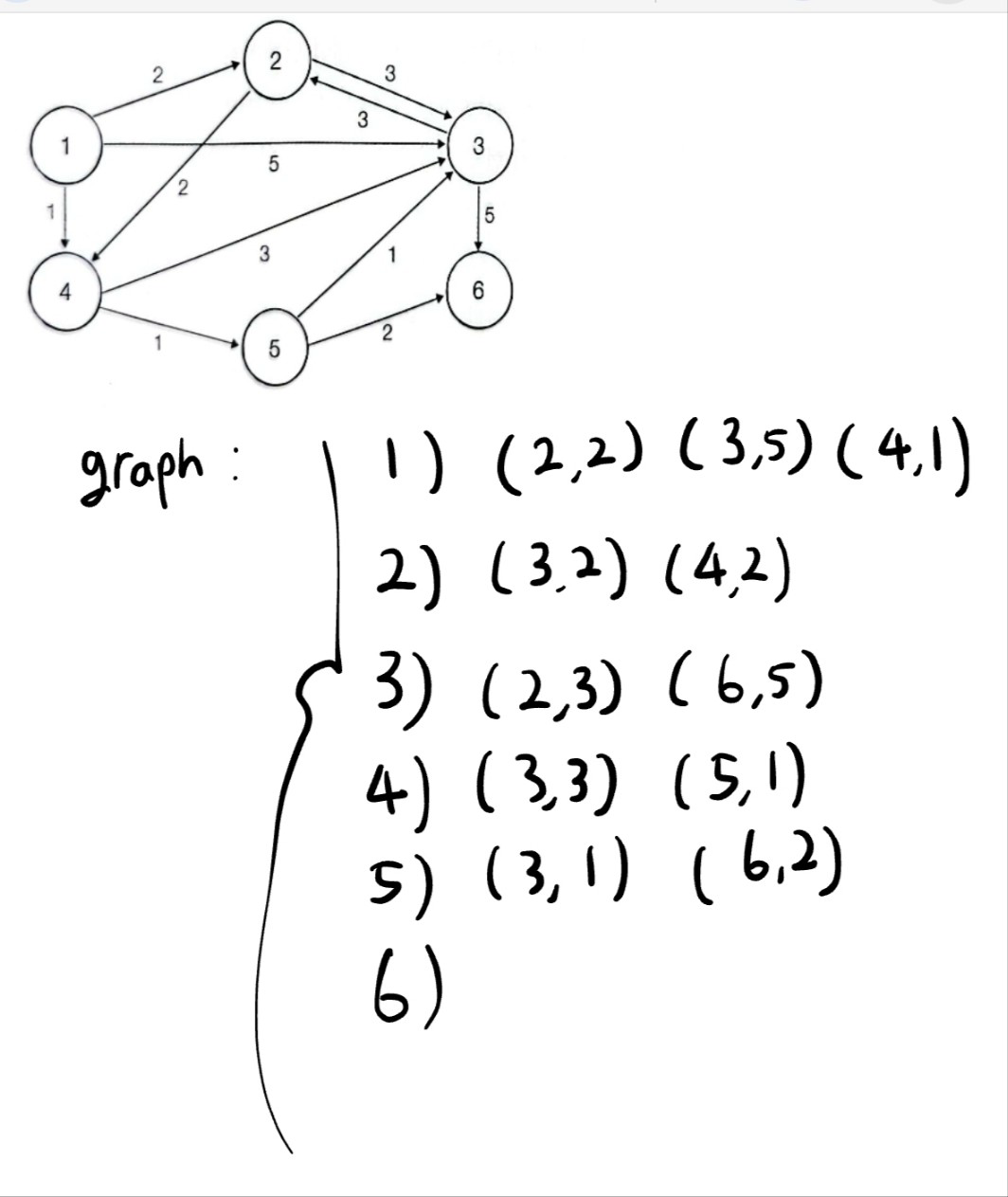
이거이다. 각각이 어디에 연결되어있는지를 보여준다.
def dijkstra(start):
distance[start] = 0
visited[start] = True
for j in graph[start]:
distance[j[0]] = j[1]
for i in range(n - 1):
now = get_smallest_node()
visited[now] = True
for j in graph[now]:
cost = distance[now] + j[1]
if cost < distance[j[0]]:
distance[j[0]] = cost
이부분은
시작 노드에서 최단 거리를 0으로 설정하고, 인접 노드들의 초기 거리를 설정한다.
반복문을 통해 최단 거리가 가장 작은 노드를 찾고, 해당 노드에서 연결된 다른 노드들의 거리를 갱신한다.
이 과정을 반복하여 모든 노드의 최단 거리를 계산한다.
def dijkstra(start):
q = []
heapq.heappush(q, (0, start))
distance[start] = 0
while q:
dist, now = heapq.heappop(q)
if distance[now] < dist:
continue
for i in graph[now]:
cost = dist + i[1]
if cost < distance[i[0]]:
distance[i[0]] = cost
heapq.heappush(q, (cost, i[0]))우선순위 큐에 시작 노드를 삽입하고, 시작 노드의 최단 거리를 0으로 설정한 후 큐에서 꺼내면서 최단 거리를 계산한다.
큐에서 꺼낸 노드의 최단 거리와 연결된 노드들의 거리 계산 후, 더 짧은 거리가 있으면 큐에 다시 삽입하여 업데이트한다.
이 과정을 큐가 빌 때까지 반복하여 모든 노드의 최단 거리를 계산한다.
오늘은 최단거리 구하기를 알아보았다.
이건 자다가도 깨어나서 할수있을만큼 잘해야한다고한다.
화이팅

