[ algorithm] Kruskal Algorithm

최소 비용 신장 트리를 O(ElogV) O(ElogV)만에 구하는 알고리즘이다.

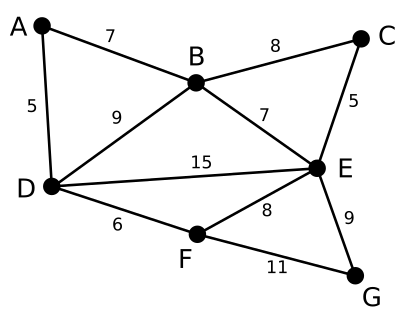
이렇게 보고 작은것부터 생각을 합시다.





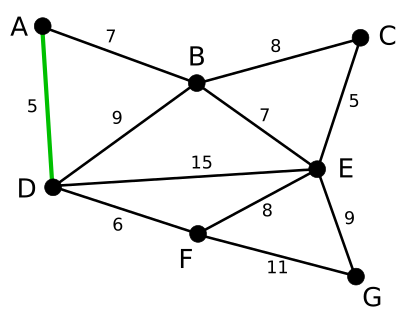
AD 와 CE 가 가장 짧은(가중치가 가장 작은) 변이다. 아무거나 골라서 AD를 선택한다. AD의 색을 변경하였다.





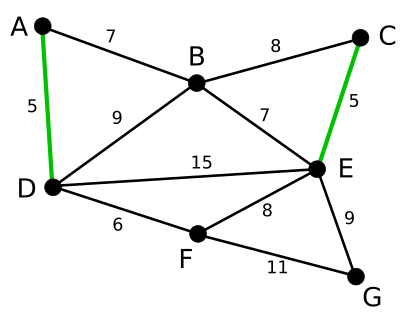
이제, CE가, 가중치가 5로서, 고리(loop)를 생성하지 않는 가장 짧은 변이다. CE의 색을 변경하였다.





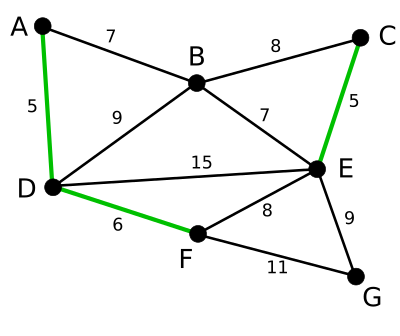
같은 방식으로 고르면 다음 변은 DF이다. 가중치는 6이다.





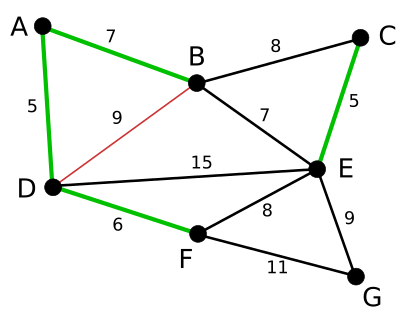
다음으로 가장 짧은 변은 AB와 BE인데, 둘 다 길이가 7이다. 임의로AB를 골랐다.
BD는 빨강색으로 변경하였는데, ABD를 연결시키면 루프를 이루기 때문이다.





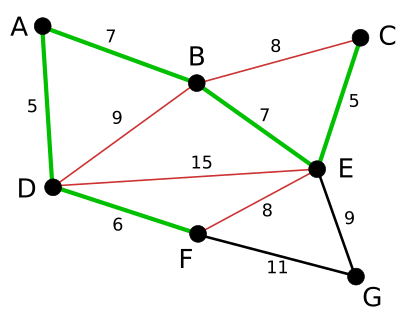
다음으로 가장 짧은 변은 BE로서 길이 7이다. 더 많은 변들이 빨강으로 변했다. BCE 루프를 생성하기 때문에
BC가 빨강색으로 변했으며, DEBA 루프를 생성하기 때문에 DE가 빨강색으로 변했고,
FEBAD 고리를 생성하기 때문에 FE가 빨강색으로 변했다.





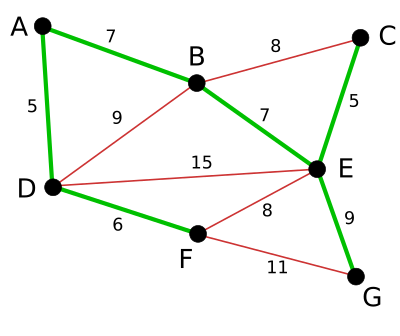
끝내, EG가 연결되면서 알고리즘이 종료된다. 최소 비용 신장 부분 그래프가 완성되었다.
이걸 코드로 구현해보면

# 특정 원소가 속한 집합을 찾기
def find_parent(parent, x):
	# 루트 노드를 찾을 때까지 재귀 호출
	if parent[x] != x:
    	parent[x] = find_parent(parent, parent[x])
    return parent[x]
    
# 두 원소가 속한 집합을 합치기
def union_parent(parent, a, b):
	a = find_parent(parent, a)
    b = find_parent(parent, b)
   	if a < b:
    	parent[b] = a
    else:
    	parent[a] = b

# 노드의 개수와 간선(Union 연산)의 개수 입력 받기
v, e = map(int, input().split())
parent = [0] * (v + 1)	# 부모 테이블 초기화하기

# 모든 간선을 담을 리스트와, 최종 비용을 담을 변수
edges = []
result = 0

# 부모 테이블 상에서, 부모를 자기 자신으로 초기화
for i in range(1, v+1):
	parent[i] = i
    
# 모든 간선에 대한 정보를 입력 받기
for _ in range(e):
	a, b, cost = map(int, input().split())
    # 비용 순으로 정렬하기 위해서 튜플의 첫 번째 원소를 비용으로 설정
    edges.append((cost, a, b))

# 간선을 비용 순으로 정렬
edges.sort()
    
# 간선을 하나씩 확인하며, 
for edge in edges:
	cost, a, b = edge
    # 사이클이 발생하지 않는 경우에만 집합에 포함
    if find_parent(parent, a) != find_parent(parent, b):
    	union_parent(parent, a, b)
        result += cost
        
print(result)

이렇게 된다.