📌 문제 : 소수 찾기
주어진 수 N개 중에서 소수가 몇 개인지 찾아서 출력하는 프로그램을 작성하시오.
⬇️ 입력
첫 줄에 수의 개수 N이 주어진다. N은 100이하이다. 다음으로 N개의 수가 주어지는데 수는 1,000 이하의 자연수이다.
⬆️ 출력
주어진 수들 중 소수의 개수를 출력한다.

💡 코드 : 소수 찾기
✅ 입력받은 수
num을 2 ~ num까지의 수로 나머지 연산을 수행. 하나라도 나누어 떨어지는 수가 있으면 소수가 아니므로 break문을 통해 반복문을 즉시 빠져나가가는데, 이 때 나누는 수가num과 같으면 소수이므로cnt++수행. 1은 소수도 합성수도 아니므로 따로 판별하지 않는다.
import java.io.*;
import java.util.StringTokenizer;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
int t = Integer.parseInt(br.readLine());
int cnt = 0;
StringTokenizer st = new StringTokenizer(br.readLine());
for(int i=1;i<=t;i++) {
int num = Integer.parseInt(st.nextToken());
for(int j=2;j<=num;j++) {
if(j == num) cnt++;
else if(num % j == 0) break;
}
}
bw.write(cnt + "");
br.close();
bw.close();
}
}➕ 다른 사람의 코드 : 소수는 자신의 제곱근보다 크지 않은 어떤 수로도 나누어지지 않는다는 특징을 가진다! 따라서, for문을 num까지 돌릴 필요 없이
Math.sqrt(num)메서드를 활용하여 제곱근 이전까지 나누어지지 않는다면 그 수는 소수이다.
import java.io.*;
import java.util.StringTokenizer;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
int t = Integer.parseInt(br.readLine());
int cnt = 0;
StringTokenizer st = new StringTokenizer(br.readLine());
for(int i=1;i<=t;i++) {
boolean isPrime = true; // 소수이면 true
int num = Integer.parseInt(st.nextToken());
if(num == 1) continue;
for(int j=2;j<=Math.sqrt(num);j++) {
if(num % j == 0) isPrime = false;
}
if(isPrime) cnt++;
}
bw.write(cnt + "");
br.close();
bw.close();
}
}
📌 문제 : 소수
자연수 M과 N이 주어질 때 M이상 N이하의 자연수 중 소수인 것을 모두 골라 이들 소수의 합과 최솟값을 찾는 프로그램을 작성하시오.
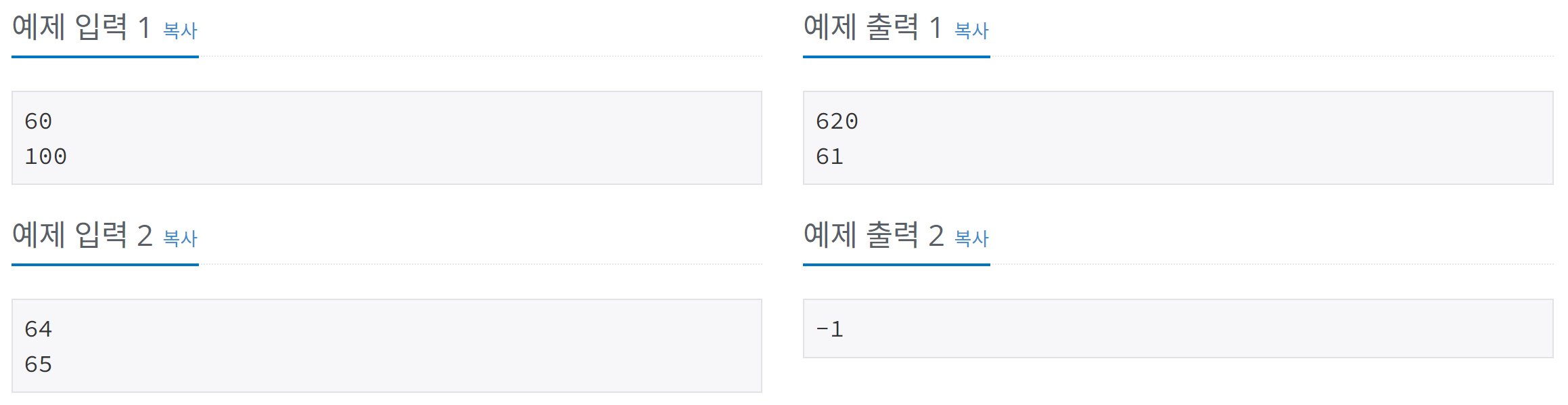
예를 들어 M=60, N=100인 경우 60이상 100이하의 자연수 중 소수는 61, 67, 71, 73, 79, 83, 89, 97 총 8개가 있으므로, 이들 소수의 합은 620이고, 최솟값은 61이 된다.
⬇️ 입력
입력의 첫째 줄에 M이, 둘째 줄에 N이 주어진다.
M과 N은 10,000이하의 자연수이며, M은 N보다 작거나 같다.
⬆️ 출력
M이상 N이하의 자연수 중 소수인 것을 모두 찾아 첫째 줄에 그 합을, 둘째 줄에 그 중 최솟값을 출력한다.
단, M이상 N이하의 자연수 중 소수가 없을 경우는 첫째 줄에 -1을 출력한다.
💡 코드 : 소수
✅ 소수를 찾아내는 알고리즘 자체는 위 문제의 ➕ 코드와 같다. for문을 통해 n ~ m까지의 수를 2 ~ i의 제곱근까지의 수로 나머지 연산을 수행하여, 소수인 경우
sum에 누적합을 수행하여 합계를 구하고, 소수를 저장하는prime에 요소를 추가해준다.
반복이 종료되면prime의 크기를 판별하여prime.size() != 0인 경우, 즉, 소수가 하나라도 존재하는 경우에는sum과 최솟값을 출력하고, 소수가 존재하지 않는 경우에는 -1을 출력한다. 최솟값의 경우, 반복문이 작은 수 ➡️ 큰 수의 순서로 수행되어 저장되는 순서도 작은 수 ➡️ 큰 수이므로, 가장 먼저 저장된 0번 인덱스의 수가 최솟값이 된다!
import java.io.*;
import java.util.ArrayList;
import java.util.List;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
int n = Integer.parseInt(br.readLine());
int m = Integer.parseInt(br.readLine());
List<Integer> prime = new ArrayList<Integer>();
int sum = 0;
for(int i=n;i<=m;i++) {
boolean isPrime = true;
if(i == 1) continue;
for(int j=2;j<=Math.sqrt(i);j++) {
if(i % j == 0) isPrime = false;
}
if(isPrime) {
sum += i;
prime.add(i);
}
}
StringBuilder sb = new StringBuilder();
if(prime.size() != 0) {
sb.append(sum).append("\n").append(prime.get(0));
} else {
sb.append("-1");
}
bw.write(sb + "");
br.close();
bw.close();
}
}


