💡 동적 계획법 (DP)
큰 문제를 작은 문제들로 나누어서 해결하는 방식
: 작은 문제들을 풀어 결과를 저장하고, 저장된 결과값을 사용하여 큰 문제를 해결한다. ➡️ 점화식 세우기!
📒 재귀 VS DP
재귀 함수를 호출하는 방식은 DP와 유사하지만, 재귀 함수는 작은 문제들이 반복되어 호출되므로 비효율적이다.
📝 하향식 (Top-down) 접근
큰 문제 ➡️ 작은 문제 : 재귀 함수
ex) 피보나치 수열
static int fib(int n) { // 재귀
if(n == 1 || n == 2) {
cnt1++; return 1;
}
else return fib(n-1) + fib(n-2);
}
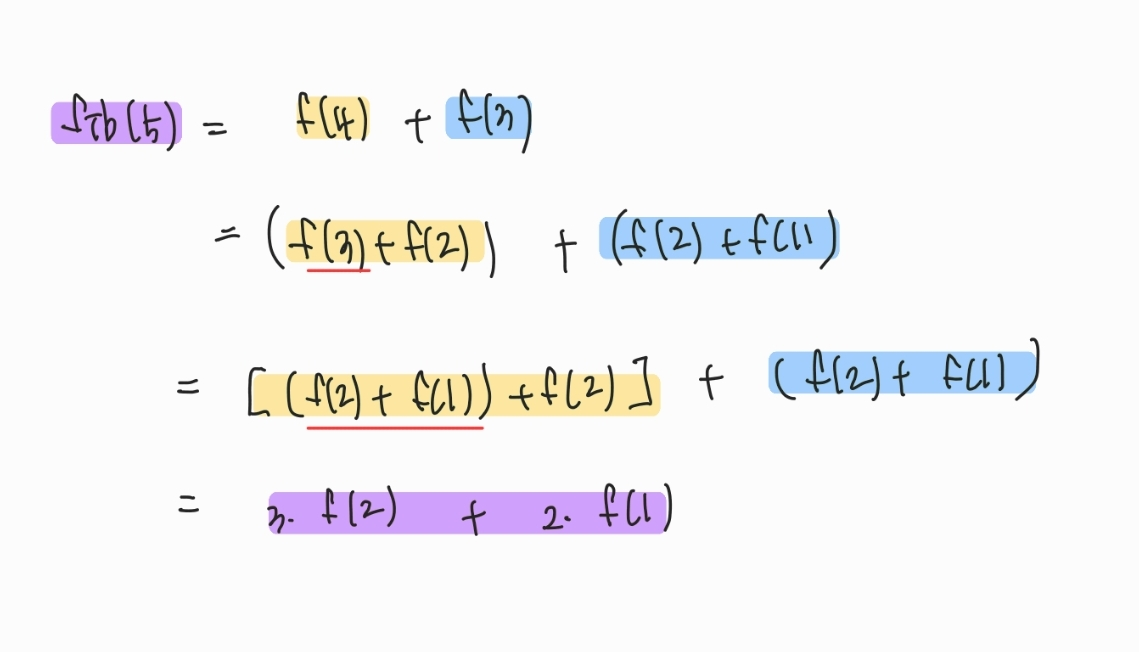: 위 코드는 피보나치 수열을 재귀 함수를 사용하여 풀이하였다. 가장 큰 문제인 fib(5)가 주어지면 작은 문제 fib(4) + fib(3)를 수행하게 된다. 이 때, 호출된 fib(4)와 fib(3) 에 대해서도 fib(n-1) + fib(n-2)를 호출하기 때문에 작은 문제들이 중복되어 수행 시간이 기하급수적으로 늘어난다는 단점이 있다.
📝 상향식 (Bottom-up) 접근
작은 문제 ➡️ 큰 문제 : 반복문 (Memoization)
✅ Memoization 기법
: DP를 구현하는 방법의 한 종류이다. 한 번 계산한 작은 문제의 결과를 메모리 공간에 저장(캐싱, Caching) 해두고, 이후 문제에서 해당 결과값을 필요로 하면 저장된 결과를 호출하여 중복 수행을 피할 수 있다.
ex) 피보나치 수열
static int fibonacci(int n) { // 동적 프로그래밍
arr[0] = arr[1] = 1;
for(int i=2;i<n;i++) {
cnt2++;
arr[i] = arr[i-1] + arr[i-2];
}
return arr[n-1];
}
: 위 코드는 DP를 활용하여 피보나치 수열을 해결하였다. 가장 작은 문제인 첫번째, 두번째 숫자를 미리 정의해두고, 이후 문제들을 for문을 통해 계산하였다. 이 때, 배열 arr[]을 선언하여 각 문제들의 결과값을 저장하여 이후 문제에서 해당 값을 필요로 하는 경우에 저장된 값을 호출해서 사용할 수 있다.
📒 요약
동적 계획법(DP)이란 큰 문제들을 작은 문제들로 나누어 해결하는 기법이다. 이전 결과값을 저장하여 다음 문제에 활용하므로 중복 계산을 피할 수 있지만, 결과를 저장하기 위해 추가적인 메모리를 사용하므로 문제의 크기에 따라 메모리 사용량이 커질 수 있다.
