💡 유클리드 호제법
두 개의 수가 주어졌을 때, 두 수의 최대공약수를 구하는 알고리즘
- 호제법 : 두 수가 서로 상대방의 수를 나누어서 원하는 수를 얻는 알고리즘
📝 예제
유클리드 호제법을 사용하여
24, 65의 최대공약수 구하기
-
큰 수 찾기 :
62 -
큰 수를 작은 수로 나누어 나머지 구하기 :
65 % 24 = 17 -
앞 연산에서 나눈 수를 나머지로 나누어 나머지 구하기 :
24 % 17 = 7 -
3번 과정을 반복하여 나머지가
0이 되는 식의 나누는 수가 두 수의 최대공약수가 된다!-
17 % 7 = 3 -
7 % 3 = 1 -
3 % 1 = 0➡️ 종료 : 최대공약수 =1
-
📒 코드 구현 (Java)
📝
eucd(int x, int y): 큰 수(or 나누는 수)x와 작은 수(or 나머지)y를 입력받아x % y를 수행하여 나머지z를 구한다.
기본적으로 나머지가 0일 때까지 3번 과정을 반복해야 하므로,x % y를 수행한 후 다음 연산에서 필요한 나누는 수y와 나머지z를 사용하여 재귀함수eucd(y, z)를 호출한다. 나머지가 0 (z = 0) 이면 나누는 수가 최대공약수이므로y를 반환하고 함수를 종료한다.
static int eucd(int x, int y) {
int z = x % y; // (큰 수 % 작은 수) or (나누는 수 % 나머지)
if(z == 0) return y; // 나누는 수를 최대공약수로 리턴
return eucd(y, z); // 3번 과정 반복
}📝 예제 : [2609] 최대공약수와 최소공배수
두 개의 자연수를 입력받아 최대 공약수와 최소 공배수를 출력하는 프로그램을 작성하시오.

- 최대공약수
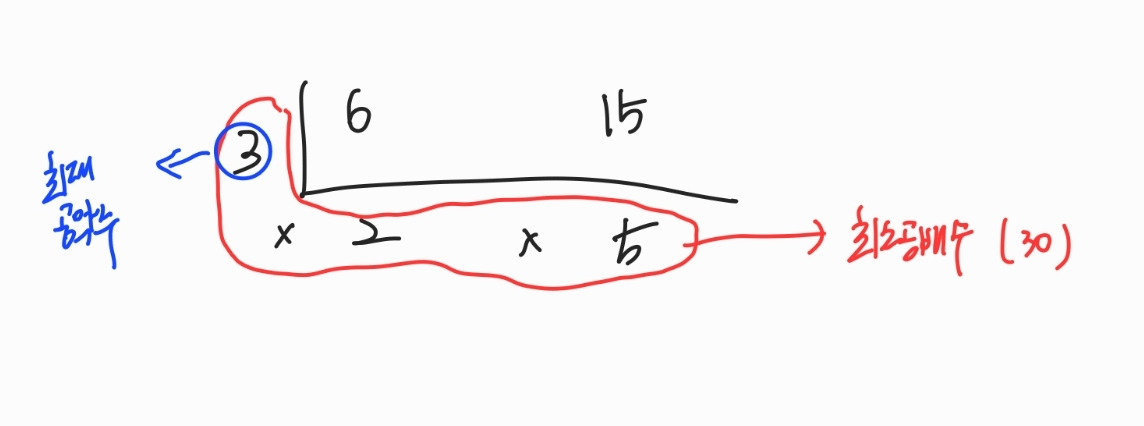
gcd: 위에서 구현한eucd(큰 수, 작은 수)메서드 사용- 최소공배수
lcm:gcd와 두 수a, b를 각각gcd로 나눈 값을 곱하여 구할 수 있음.
import java.io.*;
import java.util.*;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
StringTokenizer st = new StringTokenizer(br.readLine());
int a = Integer.parseInt(st.nextToken());
int b = Integer.parseInt(st.nextToken());
int gcd = eucd(Math.max(a, b), Math.min(a, b)); // 최대공약수
int lcm = (a/gcd) * (b/gcd) * gcd; // 최소공약수
bw.write(gcd + "\n"+ lcm);
br.close();
bw.close();
}
static int eucd(int x, int y) {
int z = x % y;
if(z == 0) return y;
return eucd(y, z);
}
}