📌 프로그래머스 Level 3 : 가장 긴 펠린드롬
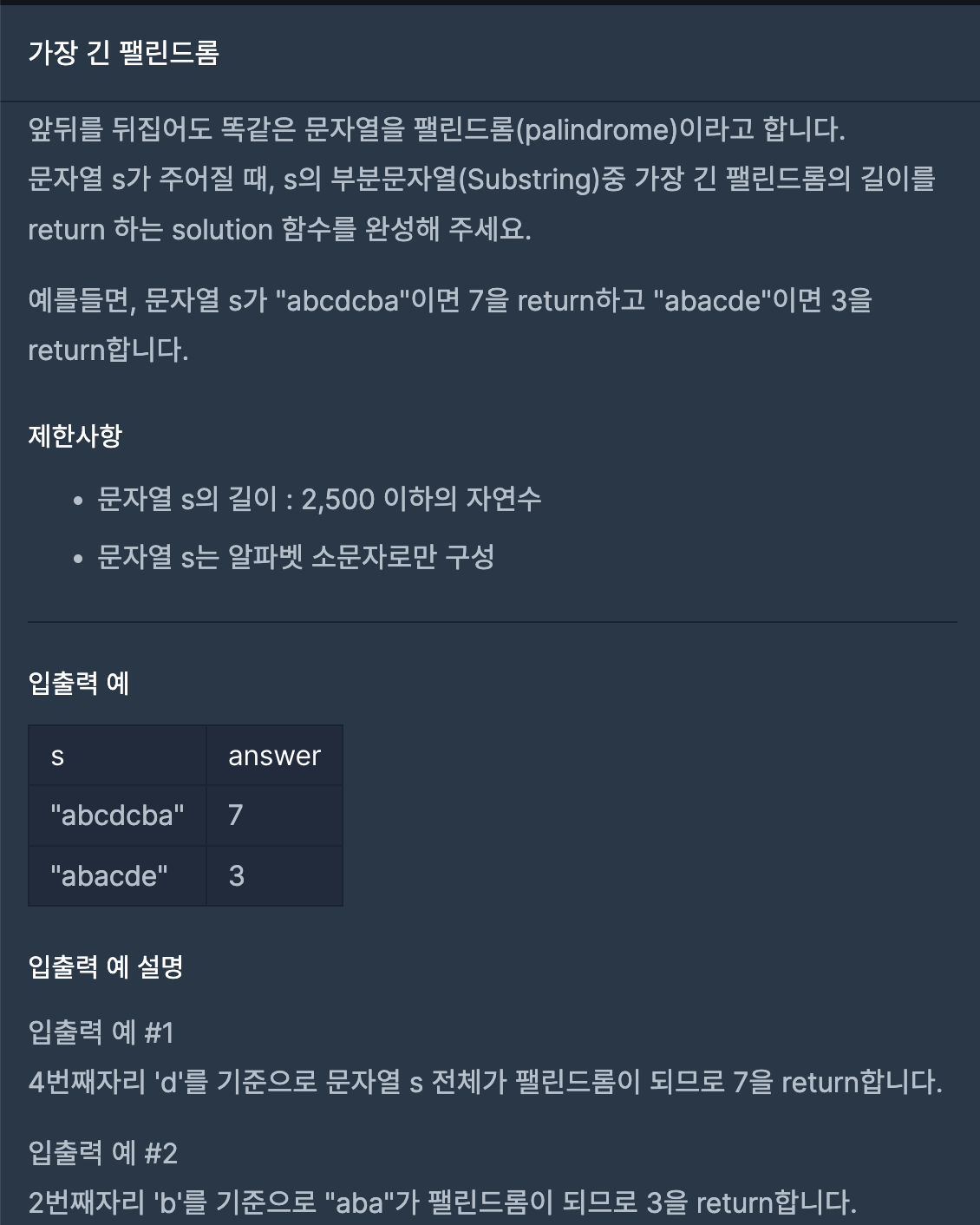
처음에 슬라이싱 사용해서 풀었는데 역시나 레벨 3라 그런지 효율성 테스트 1에서 실패했다..
최근에 이렇게 생각 없이 구현하면 시간 초과로 통과할 수 없는 문제들을 풀어서 그런지 단번에 뭐가 문젠지 알았다..
바로 슬라이싱 이 문제다!
슬라이싱을 행할 때 마다 O(슬라이싱 갯수) 복잡도를 가진다.
예를 들면 s[a:b]를 할 때마다 O(b-a)
그래서 나는 only index를 사용해서 풀었다.
사실 index만 헷깔리지 않게 짜면 꽤 금방 풀리는 문제!
📝 내 답안
def solution(s):
l = len(s)
while l != 1:
for j in range(len(s)-l+1):
cnt = 1
for i in range(l//2):
if s[j+i] == s[l+j-i-1]:
cnt+=2
else:
break
if cnt >= l:
return l
l -= 1
return 1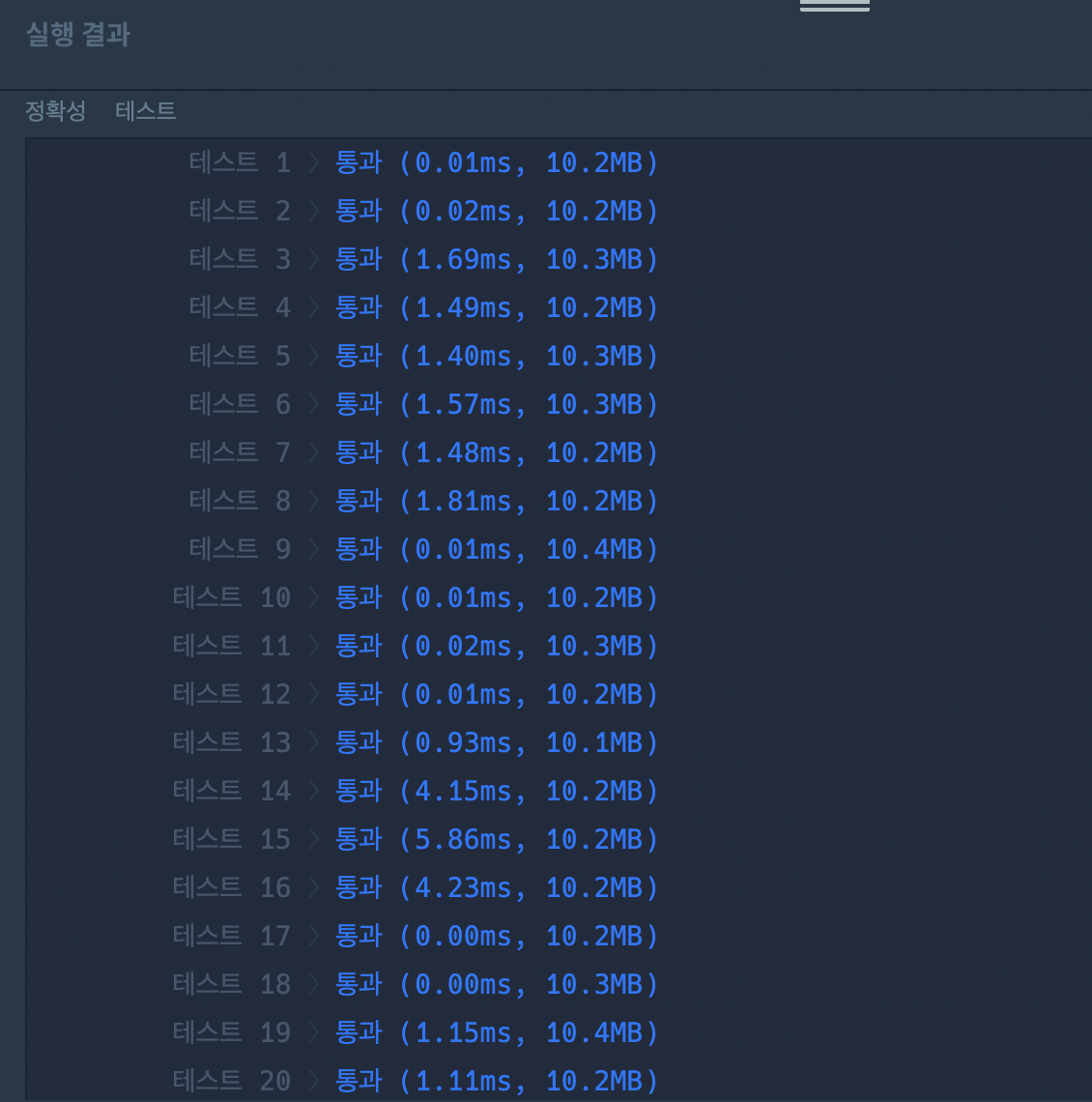
🔮 답안 해석
다음 알고리즘에 따라 구현했다.
첫 번째,
l = 최대 펠린드롬 길이(s의 길이)에서 시작해 l개의 길이를 가진 문자열에서 문자열 조합의 양 끝 index 검사해서 모두 같으면 (cnt가 l의 길이보다 크거나 같아지면) l 값 return두 번째,
두 번째, 만약 l개의 길이를 가진 문자열들이 모두 펠린드롬이 아니면
l -= 1해주고 다시 반복
def solution(s):
l = len(s)
while l != 1:
# len(s)-l+1 는 s에서 l개 문자 배열의 수(즉 조합의 시작점)
for j in range(len(s)-l+1):
cnt = 1
# 해당 문자 조합의 양 끝 비교.
# 펠린드롬이라면 양 끝이 모두 같을 것이고, 그러면 cnt가 l개를 넘게 된다.
for i in range(l//2):
if s[j+i] == s[l+j-i-1]:
cnt+=2
# 한 번이라도 같지 않으면 펠린드롬이 아니므로 더 검사할 필요가 없다
else:
break
# l개인 문자열 조합이 펠린드롬이므로 더 검사할 필요가 없다.
if cnt >= l:
return l
# 펠린드롬 만족하지 않았다면 문자열 갯수를 하나 빼주고 위 과정 반복
l -= 1
# while문에서 return 되지 않았다면 답은 1 뿐
return 1가장 헷깔릴 수 있는 부분이 바로 index 검사하는 부분이다.
중간에 for j in range(len(s)-l+1): 여기서 len(s)-l+1 은 l개의 문자열 조합이 몇 개 있는지를 뜻한다.
예를 들어 "abacde" 의 과정에서
l = 6
가능한 문자열 조합 :"abacde"(len(s)-l+1 = 6 - 6 + 1= 1가지)
펠린드롬 만족하지 않으므로 l -= 1
l = 5
가능한 문자열 조합 :"abacd", "bacde"(len(s)-l+1 = 6 - 5 + 1= 2가지)
펠린드롬 만족하지 않으므로 l -= 1
l = 4
가능한 문자열 조합 :"abac", "bacd", "acde"(len(s)-l+1 = 6 - 4 + 1= 3가지)
펠린드롬 만족하지 않으므로 l -= 1
l = 3
가능한 문자열 조합 :"aba", "bac", "acd", "cde"(len(s)-l+1 = 6 - 4 + 1= 4가지)
l = 3 일 때, "aba" 조합에서 펠린드롬을 만족하므로, l = 3 을 답으로 return
