[프로그래머스, 파이썬] 거스름돈 - 레벨 3 | DP(Dynamic Programming)

📌 프로그래머스 Level 3 : 거스름돈

문제 설명
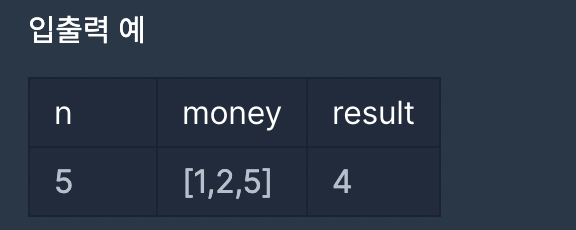
Finn은 편의점에서 야간 아르바이트를 하고 있습니다. 야간에 손님이 너무 없어 심심한 Finn은 손님들께 거스름돈을 n 원을 줄 때 방법의 경우의 수를 구하기로 하였습니다.

예를 들어서 손님께 5원을 거슬러 줘야 하고 1원, 2원, 5원이 있다면 다음과 같이 4가지 방법으로 5원을 거슬러 줄 수 있습니다.

• 1원을 5개 사용해서 거슬러 준다.
• 1원을 3개 사용하고, 2원을 1개 사용해서 거슬러 준다.
• 1원을 1개 사용하고, 2원을 2개 사용해서 거슬러 준다.
• 5원을 1개 사용해서 거슬러 준다.
• 거슬러 줘야 하는 금액 n과 Finn이 현재 보유하고 있는 돈의 종류 money가 매개변수로 주어질 때, Finn이 n 원을 거슬러 줄 방법의 수를 return 하도록 solution 함수를 완성해 주세요.

제한 사항

• n은 100,000 이하의 자연수입니다.
• 화폐 단위는 100종류 이하입니다.
• 모든 화폐는 무한하게 있다고 가정합니다.
• 정답이 커질 수 있으니, 1,000,000,007로 나눈 나머지를 return 해주세요.

문제가 간단해보이는데 레벨 3일 경우..
시간 제한이 빡빡해서 꽤나 어려운 경우가 많은데 이 문제도 역시나 그랬다.!

대다수의 사람들이 그랬겠지만 완전탐색 후 중복 제거로 구하면 시간초과로 해당 문제를 통과할 수 없다.

dp를 활용해서 풀어야하는 문제인데, dp로 다시 풀었는데도 막상 실행하면 통과를 못해서 결국 구글링의 힘을 빌렸다..

📝 내 답안

def solution(n, money):
    money.sort()
    dp = [0 for _ in range(n+1)]
    dp[0] = 1
    
    for m in money:
        for cur in range(1,n+1):
            if m > cur:
                continue
            dp[cur] += dp[cur-m]
            
    return dp[-1]%1000000007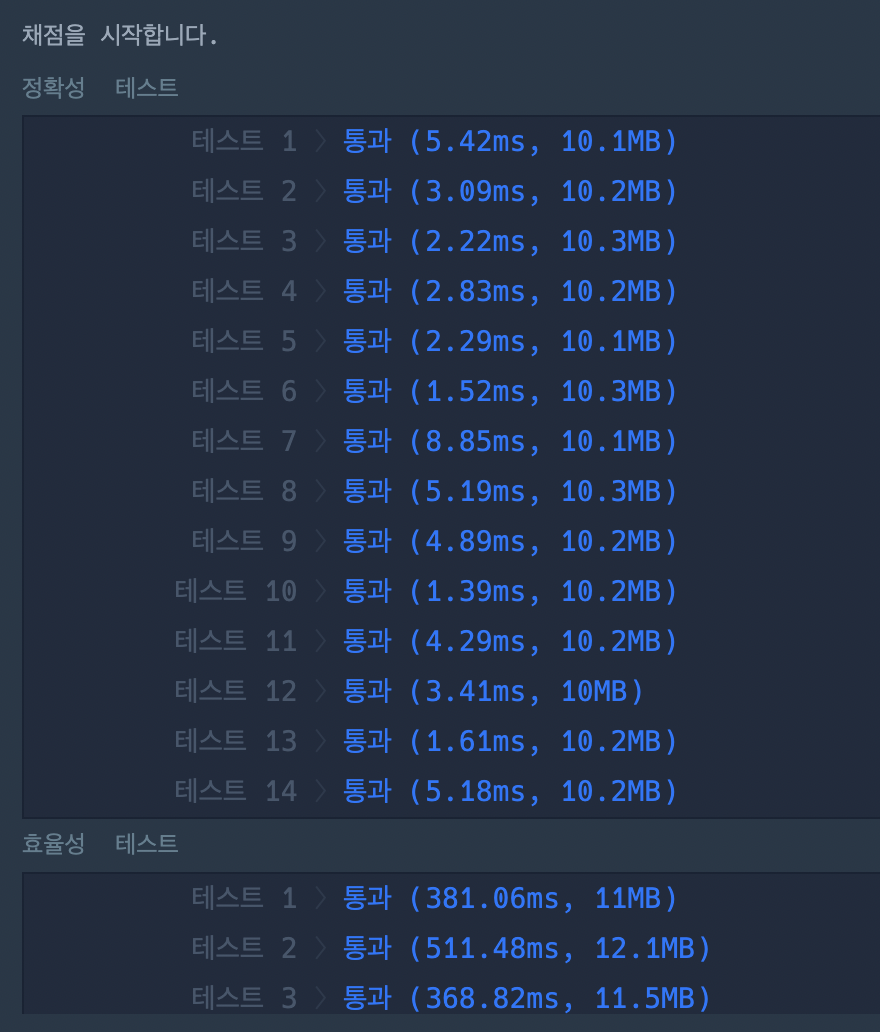

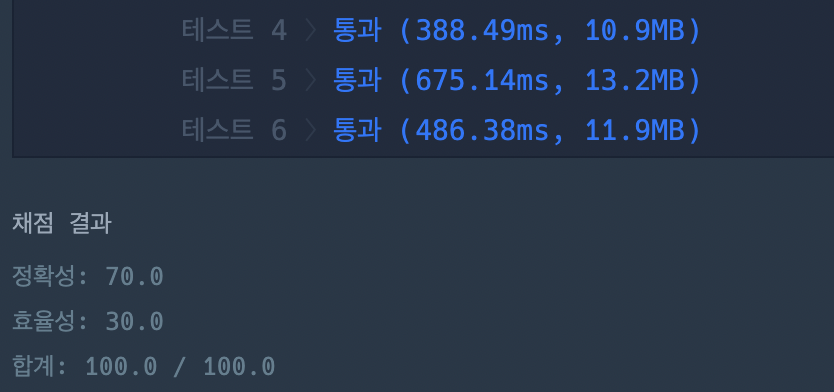
🔮 풀이

이번 문제를 풀면서 dp 알고리즘의 효율성에 놀랬고.. 천재는 많구나.. 싶었다

내가 해당 문제를 푼 알고리즘을 전개하면 다음과 같다.

❗️ 예시 TestCase

n = 5
money = [1,2,5]

📣 초기 상태

• 1원부터 n원까지 money 배열로 만들 수 있는 조합의 가짓수를 dp 배열에 담기 위해, dp 배열 정의

    dp = [0 for _ in range(n+1)]
    dp[0] = 1

dp = [1, 0, 0, 0, 0, 0]

dp[1]은 money 배열로 1원을 만들 수 있는 조합을 담는다. (목표 액수 = 1원)
...
dp[5]은 money 배열로 5원을 만들 수 있는 조합을 담는다. (목표 액수 = 5원)

• 우리의 최종 목표는 dp[5] (=dp[n]) 를 구하는 것!

여기서 dp[0] = 1 인 이유는 뒤에서 자세히 설명.

📣 조합 가짓 수 채워 넣기

• 점화식 : dp[목표 액수] += dp[목표 액수 - 현재 money]
  => dp[cur] += dp[cur - m]

이런 점화식을 사용하는 이유?

1,2,5원이 있을 때, 1원부터 5원까지의 조합을 찾아보면

• 1원을 만들기 위한 조합 => 1원 사용해서 1가지
• 2원을 만들기 위한 조합 => 1원 사용해서 1가지 + 2원 사용해서 1가지 = 2가지
• 3원을 만들기 위한 조합 => 1원 사용해서 1가지 + 1원과 2원 사용해서 1가지 = 2가지
• 4원을 만들기 위한 조합 => 1원 사용해서 1가지 + 1원과 2원 사용해서 2가지 = 3가지
• 5원을 만들기 위한 조합 => 1원 사용해서 1가지 + 1원과 2원 사용해서 2가지 + 5원 사용해서 1가지 = 4가지

    for m in money:
        for cur in range(1,n+1):
            if m > cur:
                continue
            dp[cur] += dp[cur-m]

n = 5
money = [1,2,5]
dp = [1, 0, 0, 0, 0, 0]
의 초기 상태에서,

처음 for문이 돌면

m = 1 ;
cur = 1 => dp[1] += dp[1 - 1], dp[1] += dp[0], dp[1] = 1

여기서 dp[0]을 미리 1로 지정해주는 이유가 나온다.

money가 목표 액수와 같을 경우 dp[목표액수-현재 money]가 0이 되므로 dp[0] = 1 로 지정해주어 dp[0]이 될 경우 1을 더할 수 있도록 해준다.

cur = 2 => dp[2] += dp[2 - 1], dp[2] += dp[1], dp[2] = 1
cur = 3 => dp[3] += dp[3 - 1], dp[3] += dp[2], dp[3] = 1
cur = 4 => dp[4] += dp[4 - 1], dp[4] += dp[3], dp[4] = 1
cur = 5 => dp[5] += dp[5 - 1], dp[5] += dp[4], dp[5] = 1

>>> dp = [1, 1, 1, 1, 1, 1]

두 번째 반복

m = 2 ;
cur = 1 => 현재 money인 m이 더 크므로 건너뜀
cur = 2 => dp[2] += dp[2-2], dp[2] += dp[0], dp[2] = 1(기존)+1 = 2
cur = 3 => dp[3] += dp[3-2], dp[3] += dp[1], dp[3] = 1(기존)+1 = 2
cur = 4 => dp[4] += dp[4-2], dp[4] += dp[2], dp[4] = 1(기존)+2 = 3
cur = 5 => dp[5] += dp[5-2], dp[5] += dp[3], dp[5] = 1(기존)+2 = 3

>>> dp = [1, 1, 2, 2, 3, 3]

세 번째 반복(마지막)
m = 5 ;
cur = 1,2,3,4 => 건너뜀
cur = 5 => dp[5] += dp[5-5], dp[5] += dp[0], dp[5] = 3(기존) + 1 = 4

>>> dp = [1, 1, 2, 2, 3, 4]

5원을 money 배열로 조합할 수 있는 가짓수는 총 4가지라는 것을 알 수 있다.