[프로그래머스, 파이썬] 게임 맵 최단거리 - Level 2 | 깊이/너비 우선 탐색(DFS/BFS), Deque로 풀기

📌 프로그래머스 레벨2 - 게임 맵 최단거리

<내 답안>

from collections import deque
def solution(maps):
    answer = 0
    dx = [1,0,-1,0]
    dy = [0,1,0,-1]
    goal_x = len(maps)-1
    goal_y = len(maps[0])-1
    q = deque()
    q.append((0,0))
    while q:
        x,y = q.popleft()
        for i in range(4): #4방향으로 움직여야함
            newx = x + dx[i]
            newy = y + dy[i]
            if 0<=newx<=goal_x and 0<=newy<=goal_y and maps[newx][newy] == 1:
           #범위 에러때문에 maps[newx][newy] 조건이 뒤에 쓰여져야함..!!!
                maps[newx][newy] = maps[x][y]+1
               #지나간 경로에 지나왔던 칸 수를 누적해서 쌓아줌
                q.append((newx,newy)) 
   #최종 도착지(상대 팀 진영)에 쌓인 최종 칸 수를 return, 단 1보다 작으면(= 도착할 수 있는 경로가 없음) -1 return
    return maps[goal_x][goal_y] if maps[goal_x][goal_y] > 1 else -1

<답안 설명>

q에 지나갈 수 있는 경로가 쌓이는데 결국 중간의
'maps[newx][newy] == 1'조건으로 인해 최단 경로만 남고 나머지는 소멸된다.


해당 경로로 지나가면 그 경로에 지나왔던 칸 수를 저장해놓기 때문이다.
(maps[newx][newy] = maps[x][y]+1 조건으로 인해)


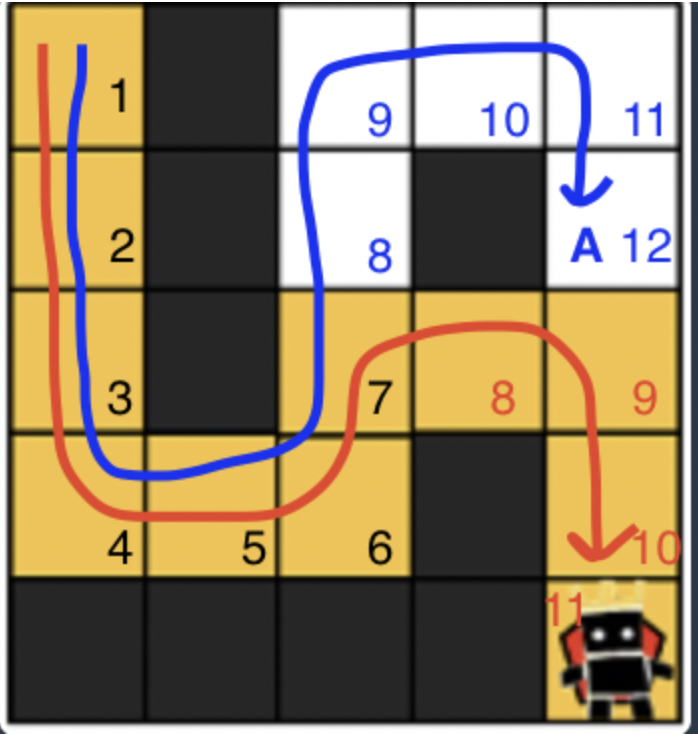
아래 그림을 보면 이해가 쉬운데, 7칸이 쌓이는 곳에서 경로가 분기되고,
이 때 q에는 두 가지 값이 존재한다.
q에는 파란색 경로의 좌표와 빨간색 경로의 좌표 두 개가 쌓인다.



하지만 파란색 경로의 좌표 중 A 지점에서 다음 지점으로 넘어가지 못하는데, 이는 주변 경로 중에 1의 값을 가진 경로가 없기 때문이다.
(maps[newx][newy] == 1이어야 다음 탐색)


반대로 빨간색 경로의 좌표는 최단 경로이기 때문에, 다른 경로의 방해 없이 최종 목적지에 도달할 수 있다.

일종의 땅따먹기같은 풀이 방법이다. 먼저 선점해야 나아갈 수 있는..

회사를 다니면서 공부를 시작해서인지 자꾸만 맘이 느슨해진다..ㅋㅋ

하루에 한 문제라도 풀도록 노력해야겠다!