[프로그래머스, 파이썬] 햄버거 만들기 - 레벨 1 | 슬라이싱 활용하기

📌 프로그래머스 레벨1 - 햄버거 만들기

가볍게 사내 코테 준비하던 중 못풀어봤던 레벨 1 문제가 있어서 풀어봤다!

내가 생각하기에.. 1레벨은 아닌거같고 2레벨에서 조금 쉬운문제? 같다..

왜냐하면 너무 생각없이 풀면 시간초과가 뜰 수 있기 때문이다.

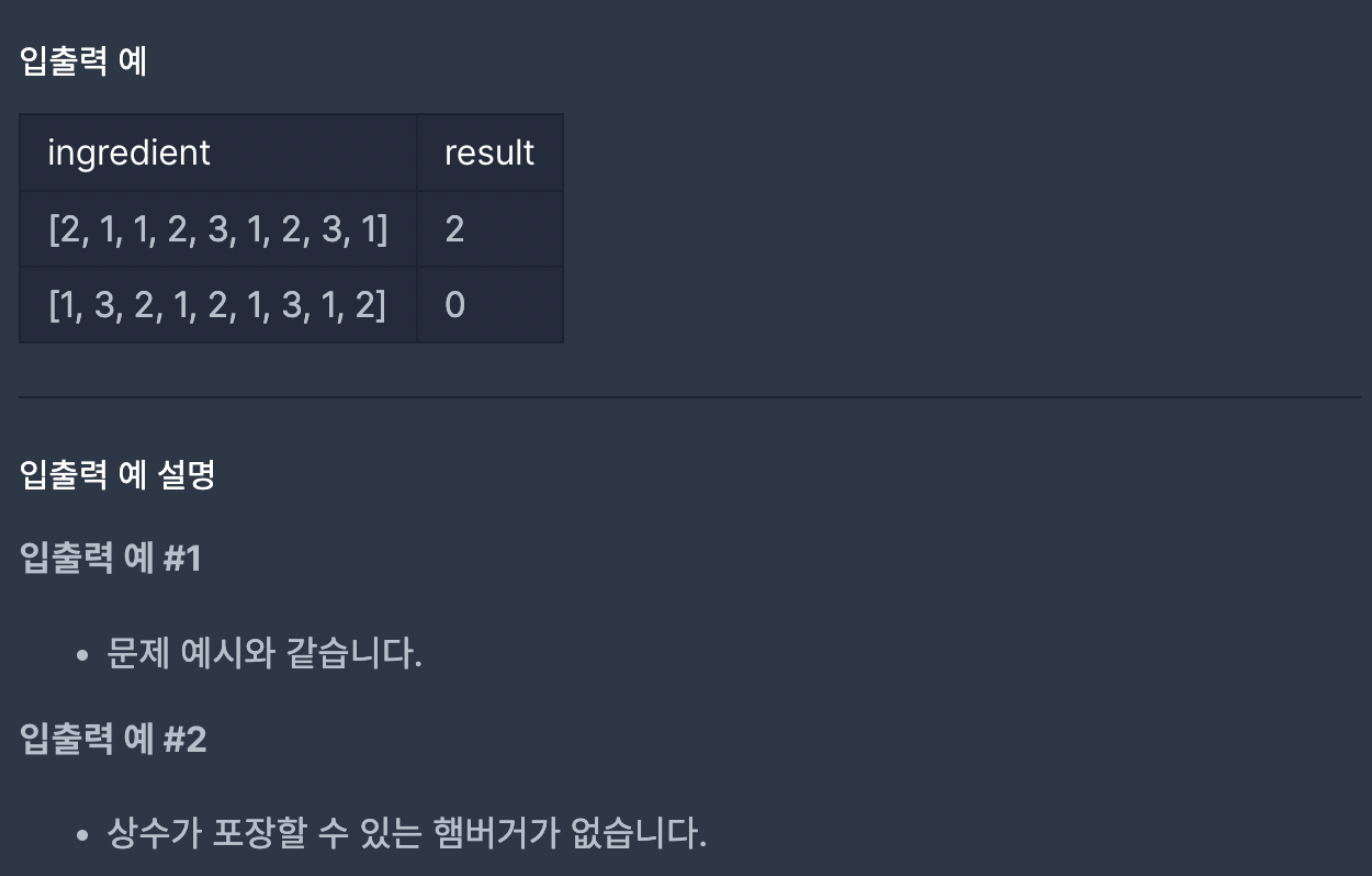
ingredient는 재료 조합이다.

순서대로 '빵(1), 야채(2), 고기(3), 빵(1)' 이 쌓여야 햄버거 하나를 완성할 수 있다.

즉, ingredient가 4개 미만이면, 무조건 햄버거를 하나도 만들 수 없으니 0을 반환해야한다..!

[빵, 빵, 야채, 고기, 빵, 야채, 고기, 빵]
배열에서 중간 음영 표시된 부분으로 햄버거 하나를 완성하면,

[빵,          야채, 고기, 빵] 이 남아서 결국 햄버거를 하나 더 만들 수 있는
[빵, 야채, 고기, 빵] 조합이 완성된다.

즉, 한 번 배열을 순회했을 때 햄버거를 만들 수 있는 순서를 슬라이싱으로 제거하고, 다시 탐색하면 답을 찾을 수 있다.

하지만 햄버거를 만들고 나서 인덱스 처리가 조금 까다로웠던 문제다.

<내 답안>

def solution(ingredient):
    answer = 0
    i = 0
    while 1:
        if len(ingredient) < 4 or i >= len(ingredient)-2:
            break
        now = ingredient[i:i+4]
        if now == [1,2,3,1]:
            answer += 1
            del ingredient[i:i+4]
            i = i-3
        else:
            i += 1
    return answer

<답안 설명>

def solution(ingredient):
    answer = 0
    i = 0
    while 1:
        # 순서대로 '빵,야채,고기,빵'이 올라가야하는데 재료가 4개 이하거나
        뒤에서 두번째 순서까지 돌았을 때 while문 종료
        if len(ingredient) < 4 or i >= len(ingredient)-2:
            break
        # i번째 배열부터 i+3번째 배열까지(4개 슬라이싱)
        now = ingredient[i:i+4]
        # 만약 now가 [빵,야채,고기,빵] 조합이면 햄버거를 하나 만들 수 있으니 answer += 1
        if now == [1,2,3,1]:
            answer += 1
           # 해당 재료로 햄버거를 만들었으니, 소진한 재료 제거
            del ingredient[i:i+4]
           # 햄버거를 만든 인덱스에서 -3한 인덱스로 돌아감.(중요!!)
            i = i-3
        else:
          # 햄버거를 만들지 않았다면 인덱스를 +1해줘서 계속 탐색
            i += 1
    return answer

가장 애를 먹은 부분이 햄버거를 만들고 나서 인덱스(i) 처리였다.

처음에는 i = i-1 처리를 해줬었는데 실행해보면 반타작이었다.

생각해보니 만약 저 코드에서 햄버거를 만들고 인덱스를 -1 처리를 해주면(i=i-1)

[1, 2, 1, 2, 3, 1, 3, 1] 같은 햄버거를 2개 만들 수 있는 사례에서 에러를 유발한다는 것을 깨달았다.

<i = i-1 사용했을 때 문제점>

[1, 2, 1, 2, 3, 1, 3, 1]
   👆 현재 i = 2, 햄버거 만들었으니 i - 1해줌


[1, 2,       3, 1]
 👆 현재 i = 1, 햄버거 못만들었으니 i + 1 해줌


[1, 2,       3, 1]
         👆 현재 i = 2, 남은 재료가 4개 미만이므로 햄버거를 만들 수 없어서 끝. ( i >= len(ingredient)-2 가 break 조건으로 인해 종료)

이렇게 남아있는 재료가 [1, 2, 3, 1]로, 햄버거 하나를 더 만들 수 있음에도 만들지 못하고 지나가버린다.

이 때, 햄버거를 만들고 나서 i - 3을 해주면 해결할 수 있다.

햄버거를 만들 수 있는 재료는 4개.

현재 인덱스에서 햄버거를 만들 수 있다면 현재 인덱스 i에서 -3인 곳까지는 햄버거를 만들 수 있는 시작 재료, 빵(1)을 만날 가능성이 있다.

그래서

햄버거를 만들고 인덱스를 -3 처리해주면(i = i -3)

[1, 2, 1, 2, 3, 1, 3, 1] 사례에서 다음과 같은 과정을 거친다.

<i = i-3 사용했을 때>

[1, 2, 1, 2, 3, 1, 3, 1]
   👆 현재 i = 2, 햄버거 만들었으니 i - 3해줌


[1, 2,       3, 1]
 👆 현재 i = 1, 햄버거 못만들었으니 i + 1 해줌.
(이 때 i >= len(ingredient)-2 조건에는 해당하지 않아서 break 되지 않는다. 만약 i=2였으면 해당 됨.)


[1, 2,       3, 1]
👆 현재 i = 0, i에서 i+3까지가 1,2,3,1 로, 햄버거를 만들 수 있는 조합이므로 answer += 1

결과적으로 2개의 햄버거를 만들 수 있다고 정상적인 답을 도출해낼 수 있다.