[프로그래머스, 파이썬] 숫자 타자 대회 - 레벨 3 | 동적 계획법(DP)

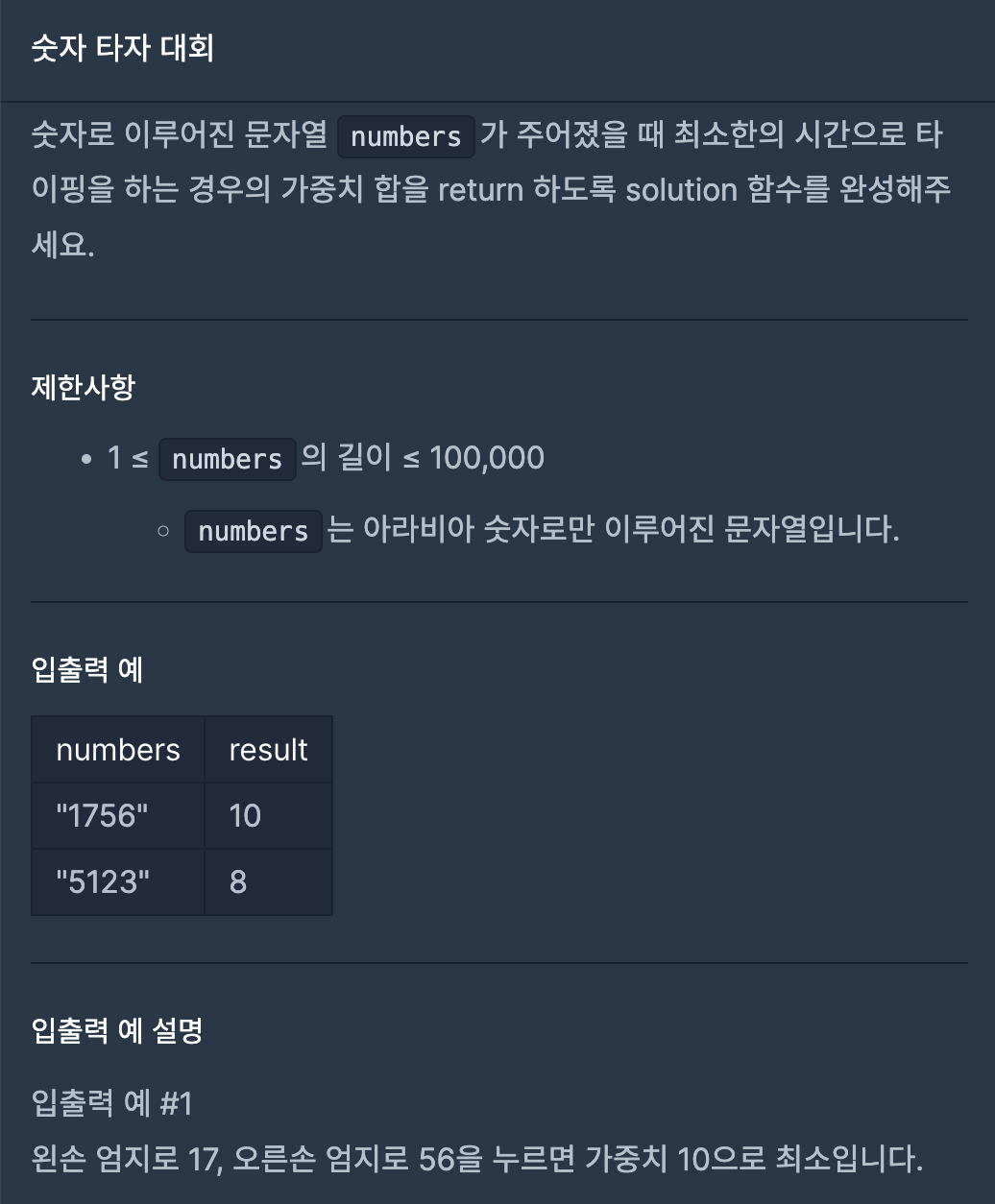
📌 프로그래머스 Level 3 : 숫자 타자 대회

DP 중 Top down 방법으로 풀어야한다. memoization(메모이라이제이션) 특성을 가지고 있다.

memoization : 컴퓨터 프로그램이 동일한 계산을 반복해야 할 때, 이전에 계산한 값을 메모리에 저장함으로써 동일한 계산의 반복 수행을 제거하여 프로그램 실행 속도를 빠르게 하는 기술.

처음에 dfs로 모든 경로 탐색해서 최소값 얻어내는 방식으로 풀었다가 시간초과로 풀지 못했다.

📝 내 답안

from collections import deque
def solution(numbers):
    answer = 0
    m = {}
    # 가중치 map
    m['0'] = [1, 7, 6, 7, 5, 4, 5, 3, 2, 3]
    m['1'] = [7, 1, 2, 4, 2, 3, 5, 4, 5, 6]
    m['2'] = [6, 2, 1, 2, 3, 2, 3, 5, 4, 5]
    m['3'] = [7, 4, 2, 1, 5, 3, 2, 6, 5, 4]
    m['4'] = [5, 2, 3, 5, 1, 2, 4, 2, 3, 5]
    m['5'] = [4, 3, 2, 3, 2, 1, 2, 3, 2, 3]
    m['6'] = [5, 5, 3, 2, 4, 2, 1, 5, 3, 2]
    m['7'] = [3, 4, 5, 6, 2, 3, 5, 1, 2, 4]
    m['8'] = [2, 5, 4, 5, 3, 2, 3, 2, 1, 2]
    m['9'] = [3, 6, 5, 4, 5, 3, 2, 4, 2, 1]
    
    # 위치랑 쌓인 가중치
    #(왼쪽,오른쪽,가중치)
    q = deque()
    # 경우의 수, 가중치 저장
    dic = {}
    dic[('4','6')] = 0
    
    for i in range(len(numbers)):
        n = numbers[i]
        now_dic = {}
        
        for lp,rp in dic.keys():
            q.append((lp,rp,dic[(lp,rp)]))
        
        while q:
            l,r,c = q.popleft()
            l_cnt = m[l][int(n)]
            r_cnt = m[r][int(n)]
            
            if l == n:
                # 왼쪽이 움직이고, 가중치 +1
                if (n,r) not in now_dic.keys() or now_dic[(n,r)] > c + 1:
                    now_dic[(n,r)] = c + 1
            elif r == n:
                # 오른쪽이 움직이고, 가중치 +1
                if (l,n) not in now_dic.keys()  or now_dic[(l,n)] > c + 1:
                    now_dic[(l,n)] = c + 1
                    
            else:
                # 왼쪽 움직였을 때
                if (n,r) not in now_dic.keys() or now_dic[(n,r)] > c + l_cnt:
                    now_dic[(n,r)] = c + l_cnt
                # 오른쪽 움직였을 때
                if (l,n) not in now_dic.keys() or now_dic[(l,n)] > c + r_cnt:
                    now_dic[(l,n)] = c + r_cnt
        # 기록 갱신
        dic = now_dic
    
    return min(dic.values())

나중에 다시 한 번 풀어봐야겠다.