본 포스팅은 충남대 정상근 교수님의 강의를 참고하였습니다. 개인 공부를 기록하는 목적의 포스팅이며, 문제가 될 시 삭제하겠습니다.

Principal Component Analysis(PCA)

대부분 실제로 분석하는 데이터는 많은 특성(feature)을 가지고 있다. 데이터의 특성이 많을수록 차원도 증가하게 되는데, 데이터가 고차원으로 갈수록 데이터 공간의 부피가 급격하게 커지고, 데이터간의 거리가 증가하게 된다. 이는 학습속도를 느리게 할 뿐만 아니라, 모델이 복잡해지며 오버피팅(overfitting) 위험이 커지게 된다. 따라서 데이터가 고차원일 경우, 차원축소(Dimension Reduction) 방법은 데이터를 분석하고 시각화하는데 매우 편리한 수단을 제공한다.

PCA는 영상인식에서 주로 활용되는데, 대표적으로 얼굴인식이 그 예이다. 우리나라 대표 미인들을 빠른 시간에 바꿔가며 나타내주는 영상을 본 적이 있을 것이다. 20명의 미스코리아 출신인들의 얼굴을 PCA를 이용하여 분석한 연구가 있는데, 6개의 아이젠페이스(eigenface)로 이들을 설명할 수 있다고 나타났다.

차원 축소 (Dimension Reduction)

차원 축소란, 높은 차원의 데이터 중에서 몇 가지만 골라서 새로운 (더 작은) 차원의 데이터를 만드는 것이다. 단, 원래 데이터가 가지고 있는 내재적 속성을 유지해야 한다.

차원 축소에는 다음과 같은 두 가지 방법이 있는데, 일반적으로 투영 접근법이 사용된다.

• Feature Selection

  • 가공하지 않고 그대로 selection해서 사용한다.

• Feature 투영(Projection) (Feature extraction)

• selection 후 가공하여 사용한다.

• 다양한 알고리즘이 있는데, 대표적으로 Principal component analysis (PCA)가 있다.

주성분 분석 Principal component analysis (PCA)

PCA는 분포된 데이터들의 주성분을 찾아주는 방법이다. 즉, 데이터를 가장 잘 설명할 수 있는 데이터 축을 찾는 것인데, 분산이 가장 큰 벡터를 찾는 것이고, 이는 선형변환을 통해 찾아낼 수 있다.

1. ${X}\rightarrow{Y}$ : Linear Data Projection
2. Basis Change : Linear Projection할 때 데이터가 잘 설명될 수 있는 축으로 basis를 바꿀 것이다.
3. 중복성 최소화(Minimize Redundancy) : 데이터를 사용하는 component들 끼리의 정보 중복성를 줄인다.

선형 변환 (Linear Transformation)

어떠한 matrix에 의해 방향이 바뀌지 않는 vector들이 있다. (크기만 바뀐다) = 아이젠벡터

If Every Vector is Eigenvector, then Matrix is a Multiple of Identity Matrix

직관적 이해

correlated : A가 움직일 때, D도 따라서 움직인다면 A와 D 중 하나의 정보만 필요하다

not-correlated : A가 움직일 때, D의 움직임이 별 관계가 없다면 A와 D 둘 모두의 정보가 필요하다

P를 구해 보자

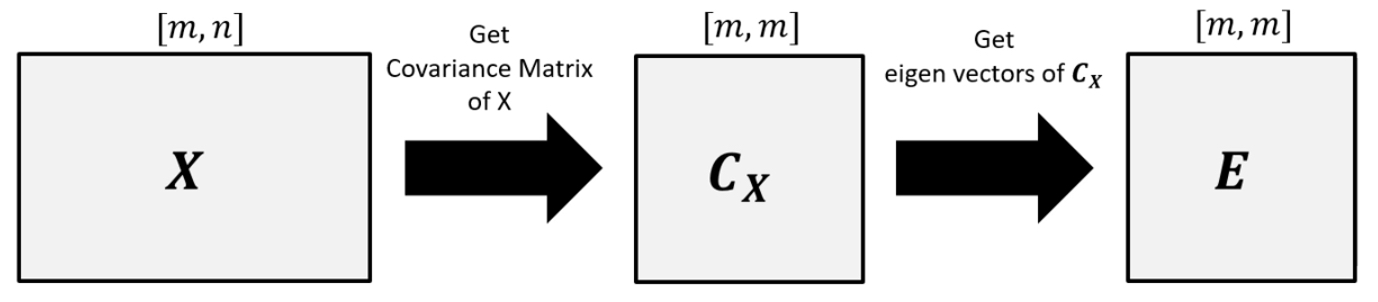
기존 행렬 X의 공분산행렬 $C_X$를 구한다.

$C_X$의 $E·v (Eigenvector)$를 구한다. (여러개)

각각의 Eigenvector에서 $e·v(Eigen value)$를 구하여 순서대로 marix를 만들면 P가 된다.

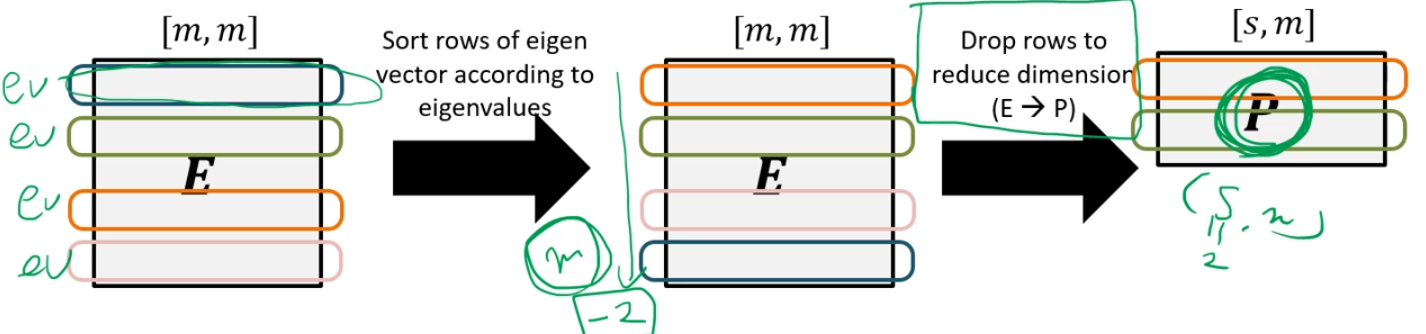
아이젠 벡터를 큰 순서대로 나열한 후, 영향력이 작은 하위 n(여기선 -2)을 제거한다.

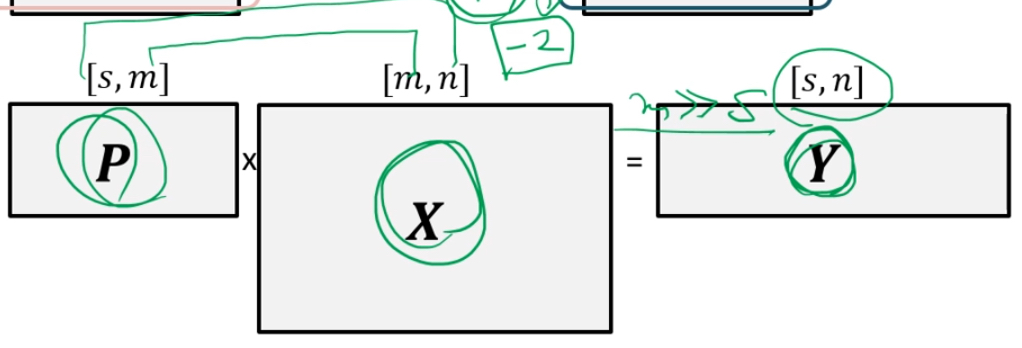
X를 가장 잘 설명할 수 있는 Y를 구할 수 있다. (X를 가장 잘 설명할 수 있는 basis로 바뀌어 Y가 되었다.)

정리

데이터가 고차원일 경우 차원 축소를 해야하는데, 차원 축소 중에서도 투영을 이용한 방법에는 대표적으로 주성분분석(PCA) 알고리즘이 있다. PCA는 데이터 셋에서 중복된 정보를 제거함으로써 변수를 줄이는데, 통계적으로 상관관계가 없도록 데이터셋을 회전시켜 차원을 축소한다.

활용

Scikit-Learn을 사용하여 PCA를 구할 수 있다.

from sklearn.decomposition import PCA
pca = PCA(n_components=3)
pca.fit(X)
print('eigen_value :', pca.explained_variance_)
print('explained variance ratio :', pca.explained_variance_ratio_)