본 포스팅은 충남대 정상근 교수님의 강의를 참고하였습니다. 개인 공부를 기록하는 목적의 포스팅이며, 문제가 될 시 삭제하겠습니다.

Distance Metric Types

거리 측정에 대한 내용은 데이터와 데이터간의 유사성을 보는 군집분석, 변수와 변수간의 관계를 보는 다변량 통계 분석 등 다양한 분야에서 기본이 된다. 우리가 일반적으로 생각하는 Pairwise(1:1) 관계에서도 거리를 측정할 수 있지만, Distribution-wise : 1 (or Many) to Many 관계에서도 거리를 측정할 수 있다.

Pairwise(1:1)

2. 코사인 거리 (Cos distance)
3. 유클리드 거리 (Euclid distance)
4. 맨하탄 거리 (Manhattan distance, City block distance)
5. 민코프스키 거리 (Minkowski distance)

코사인 거리 (Cos distance)

코사인 유사도(Cosine Similarity)는 두 개의 문서별 단어별 개수를 세어놓은 특징 벡터 X, Y 에 대해서 두 벡터의 곱(X*Y)을 두 벡터의 L2 norm (유클리드 거리)의 곱으로 나눈 값이며, 코사인 거리(Cosine Distance)는 '1 - 코사인 유사도(Cosine Similarity)'이다.

Dot product definition : $a\cdot b = \|a\|\|b\|cos\theta$

코사인 거리 : $1-cos\theta$

코사인 유사도

$cos\theta = \|a\|\|b\| \over a•b$

문서를 유사도 기준으로 분류 혹은 그룹핑을 할 때 사용한다.

유클리드 거리 (Euclid distance)

유클리드 공간에서의 기하학적 최단 거리(직선 거리)이다.

n차원에서의 유클리드 거리는 다음과 같이 나타낸다.

$d(p,q) = \sqrt{(p_1-q_1)^2 + (p_2-q_2)^2 + ... + (p_n-q_n)^2}$

맨하탄 거리 (Manhattan distance, City block distance)

격자 형태의 공간에서의 거리이다.

n차원에서의 맨하탄 거리는 다음과 같이 나타낸다.

$d_1(p,q) = ||p-q||_1 = \Sigma_{i=1}^{n}{|p_i-q_i|}$

맨하탄 도시에서 건물 블럭들이 있을 때, 몇 블럭을 이동해야 원하는 곳에 도달할 수 있는지를 측정하는 것에서 유래하였다.

민코프스키 거리 (Minkowski distance)

p-norm을 활용하여 일반화한 것으로, 맨하탄 거리와 유클리드 거리가 하나의 공식으로 표현된다.

$(\Sigma_{i=1}^n{|x_i-y_i|^p})^{1/p}$

Norm

놈(Norm)은 vector값을 scalar값으로 바꿀 수 있는 function의 일종으로, 아래의 세 가지 속성을 동시에 만족한다면 Norm( $\|v\|$ )이라 한다.

1. Zero Vector : $v = 0$
2. Scalar Factor : $f(cv) = |c|f(v)$
3. Triangle Inequality : $f(u + v) \le f(u) + f(v)$

P-norm

p를 $p \ge 1$ 인 실수라 할 때, $p-norm$ ($l_p-norm$) of vector $X = (x_1,...,x_n)$

$||X||_p = (\Sigma_{i=1}^n{|x_i|^p})^{1/p}$

$p=1$ : Manhattan norm ($l_1-norm$)

$p=2$ :Euclidean norm ($l_2-norm$)

$p=\infty$ : Maximum norm

유클리드의 경우 p가 2이고, 맨하탄의 경우 p가 1로 둘 다 민코프스키 거리에 포함된다. 즉, 민코프스키 거리를 표현한다면 다음과 같다.

민코프스키 거리 (Minkowski distance)

$X = (x_1,x_2,...,x_n)\text{and}Y = (y_1,y_2,...,y_n) \in \R^n$

$D(X,Y) = (\Sigma_{i=1}^n{|x_i-y_i|^p})^{1/p}$

$p=1$ : Taxicab (Manhattan) Distance ($l_1-distance$)

$p=2$ :Euclidean Distance ($l_2-distance$)

$p=\infty$ : Maximum norm

Distribution-wise : 1 (or Many) to Many

마할라노비스 거리(Mahalanobis distance)

정규분포에서 특정 값 X가 얼마나 평균에서 멀리있는지를 나타내는 거리로써, 관측된 X가 얼마나 일어나기 힘든 일인지를 수치화한 것이다. 즉, 평균과 표준편차를 고려했을때 얼마나 중심에서 멀리 떨어져 있는가를 나타내며, 주로 관측된 데이터의 신뢰성 또는 적합성을 판단하는데 쓰인다.

마할라노비스 거리의 주요 아이디어와 공식은 다음과 같다.

1. 각 Component들 사이의 상관관계를 없앤다.
2. Scale에 민감하지 않게 정규화해준다.
3. Euclidean처럼 거리를 계산한다.

$D_M(x,y) = \sqrt{(x-y)^TS^{-1}(x-y)}$

$x$ : 점들의 벡터 (차원에 따라 x와 y 벡터의 col 개수가 달라진다)

$y$ : 점들의 벡터

$S$ : Covariance matrix (공분산 행렬)

유클리드와 마할라노비스의 비교

유클리드는 단순히 주어진 거리만을 계산하지만

마할라노비스는 데이터의 상관성을 고려해서 거리를 계산한다.

아래 두 식은 유클리드 거리의 공식을 다르게 나타낸 것이다.

$D_{L2}(x,y) = \sqrt{(x_1-y_1)^2+(x_2-y_2)^2}$

$D_{L2}(x,y) = \sqrt{(x-y)^T(x-y)}$

유클리드 : $D_{L2}(x,y) = \sqrt{(x-y)^T(x-y)}$

마할라노비스 거리 to Center : $D_M(x,\mu) = \sqrt{(x-\mu)^TC^{-1}(x-\mu)}$

마할라노비스 거리의 일반화된 형태 : $D_M(x,y) = \sqrt{(x-y)^TS^{-1} (x-y)}$

$x-\mu$ in M to Center 은 각 component의 중심까지의 거리

$C^{-1}$ in M to Center 은 상관관계를 없애고 Scale factor를 정규화한다.

참고

공분산 행렬을 통해 직관적으로 이해할 수 있다.

Covariance Matrix ($S^{-1}$)

$x = (x_1, x_2, x_3)$

$x_1$이 변할 때 $x_2,x_3$가 변하는 정도를 확인. : n x n의 모든 선형 관계를 측정한다. Covariance로.

$Covariance(x_1,x_2) = cov(x_1,x_2)$

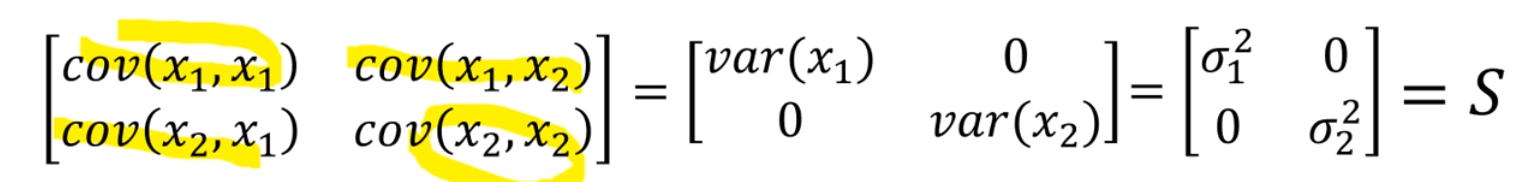
직관적으로 $\sigma$는 폭으로 생각할 수 있다.

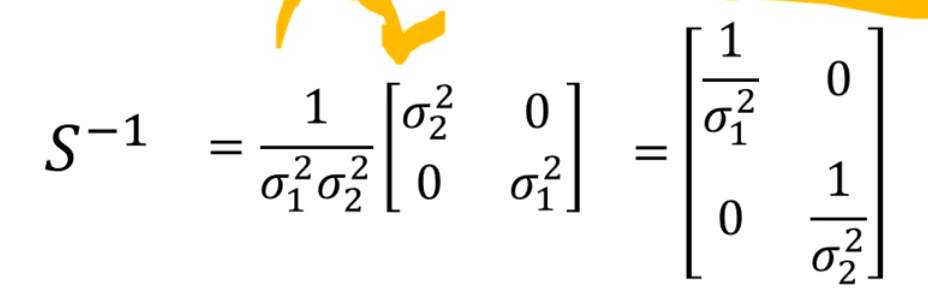
공식을 보면 공분산 행렬의 역행렬을 중간에 곱해주는데, 이것은 결국 단위 행렬의 각 행에 분산을 나누는 것과 일치한다. 즉, 상관관계를 없애주고, 스케일에 민감하지 않게 정규화 해주는 것이다.

아래는 2차원에서 no correlation일 때의 마할라노비스 공식이다.

활용

Scipy를 사용하여 거리를 구할 수 있다.

from scipy.spatial import distance
distance.euclidean([1,2],[3,0]) # 유클리드 거리
distance.cityblock([1,2],[3,0]) # 맨하탄 거리
distance.mahalanobis([1,2],[3,0]) # 마할라노비스 거리