
BOJ 9095. 1, 2, 3 더하기
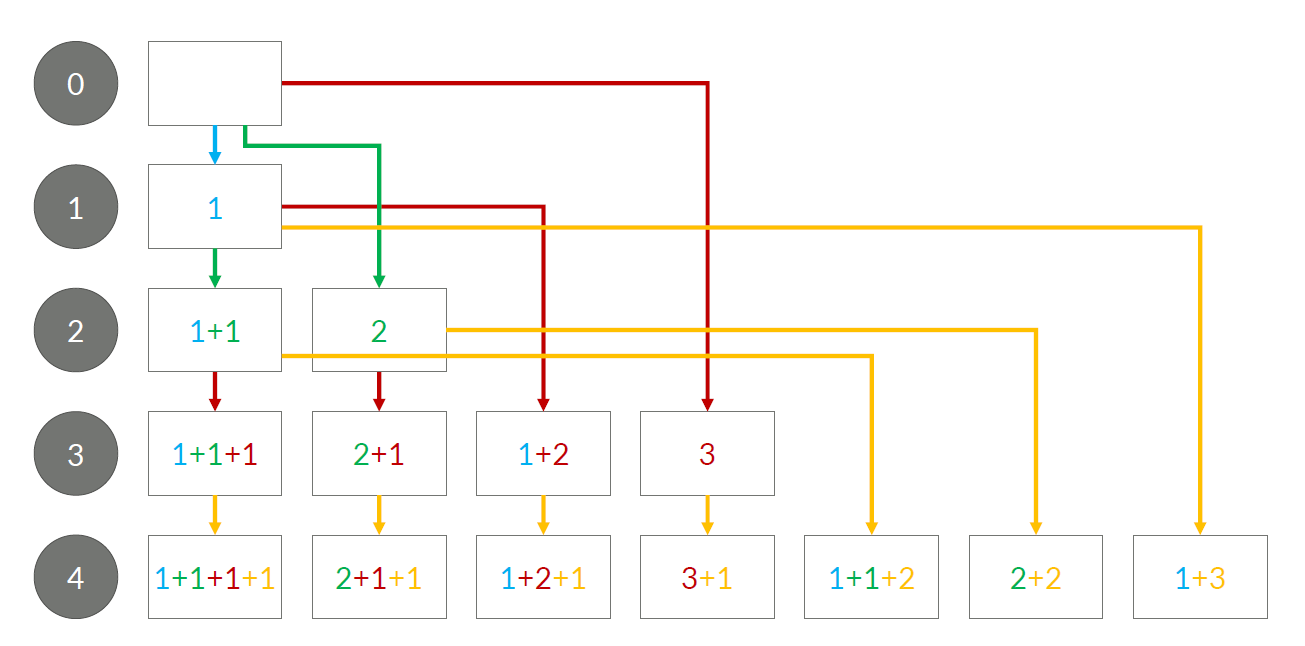
정수 4를 1, 2, 3의 합으로 나타내는 방법은 총 7가지가 있다. 합을 나타낼 때는 수를 1개 이상 사용해야 한다.
- 1+1+1+1
- 1+1+2
- 1+2+1
- 2+1+1
- 2+2
- 1+3
- 3+1
정수 n이 주어졌을 때, n을 1, 2, 3의 합으로 나타내는 방법의 수를 구하는 프로그램을 작성하시오.
1. 문제 해석
이 문제를 풀기 위해서는 각 숫자를 포함한다 or 포함하지 않는다 의 모든 경우의 수를 검사해야한다. N의 제한이 10까지이고 1, 2, 3을 포함하거나 포함하지 않으려면 3^10 = 59,049의 경우의 수가 존재한다. 이 문제의 구현방법은 세 가지가 존재한다. 그것은 반복문으로 구현, 재귀호출을 통한 구현, 동적 프로그래밍을 이용한 구현이다.
먼저, 반복문으로 구현하는 경우에는 매우 복잡한 N중 for문이 만들어진다. 이 경우에 시간복잡도는 각 반복문의 반복횟수가 3으로 고정이므로 O(3^N)이 된다.
이를 구현하는 또 다른 방법으로 재귀를 이용하는 방법이 있다. 이 경우에 오히려 반복문보다 코드가 간결하여 직관적인 이해가 가능하다. 재귀로 구현한다고 해도 시간복잡도는 반복문으로 구현하는 것과 같다. O(3^N)이다.
마지막으로, 동적 프로그래밍을 통해서도 이 문제를 해결할 수 있다. 이 경우에는 총 N번만 반복하면 동적배열이 채워지므로 시간복잡도는 O(N)으로 기하급수적인 성능향상을 보인다.
2. 문제 풀이
2.1. 반복문으로 구현
#include <iostream>
using namespace std;
int main() {
int T, n;
cin >> T;
for (int idx = 0; idx < T; idx++) {
cin >> n;
int ans = 0;
for (int l1 = 1; l1 <= 3; l1++) {
if (l1 == n) ans++;
for (int l2 = 1; l2 <= 3; l2++) {
if (l1+l2 == n) ans++;
for (int l3 = 1; l3 <= 3; l3++) {
if (l1+l2+l3 == n) ans++;
for (int l4 = 1; l4 <= 3; l4++) {
if (l1+l2+l3+l4 == n) ans++;
for (int l5 = 1; l5 <= 3;l5++) {
if (l1+l2+l3+l4+l5 == n) ans++;
for (int l6 = 1; l6 <= 3; l6++) {
if (l1+l2+l3+l4+l5+l6 == n) ans++;
for (int l7 = 1; l7 <= 3; l7++) {
if (l1+l2+l3+l4+l5+l6+l7 == n) ans++;
for (int l8 = 1; l8 <= 3;l8++) {
if (l1+l2+l3+l4+l5+l6+l7+l8 == n) ans++;
for (int l9 = 1; l9 <= 3;l9++) {
if (l1+l2+l3+l4+l5+l6+l7+l8+l9 == n) ans++;
for (int l10 = 1; l10 <= 3; l10++) {
if(l1+l2+l3+l4+l5+l6+l7+l8+l9+l10 == n) ans++;
}
}
}
}
}
}
}
}
}
}
cout << ans << endl;
}
return 0;
}물론, 앞의 코드와 같이 N중 for문으로 구현해도 정답이 나오기 때문에 저것도 정답이 된다. 하지만 실제로 조금만 반복할 대상이 복잡해져 버리면 N중 for문의 구현은 그리 쉽지가 않다. 그리고 저렇게 중복되는 코드의 반복은 좋지 않다. 따라서 그 규칙성을 파악하여 재귀로 이를 구현할 수 있다.
2.2. 재귀를 통한 구현
숫자 몇개로 N을 만들 수 있는가? 그리고 거기에 포함된 숫자는 무엇인가? 이 두가지를 조합하여 재귀함수를 모델링 해보면, go(count, sum, goal)와 같이 나타낼 수 있다. 숫자 count개로 합 sum을 만드는 경우의 수를 계속 누적해나가는 것이다.
재귀의 모델링
재귀를 구현하기 위해서 크게 세 가지 경우를 나누어 볼 수 있다. 먼저, 탈출조건으로서 정답이 불가능한경우와 정답을 찾은 경우가 있다. 그리고 반복을 위해서 다음 경우를 호출하는 경우가 있다.
1) 정답이 불가능한 경우 : sum > goal
2) 정답을 찾은 경우 : sum == goal
3) 다음 경우 호출 : go(count+1, sum+i, goal)
- 1을 사용하는 경우 : go(count+1, sum+1, goal)
- 2를 사용하는 경우 : go(count+1, sum+2, goal)
- 3을 사용하는 경우 : go(count+1, sum+3, goal)
int go(int count, int sum, int goal) {
if (sum > goal) return 0; // 불가능한 경우
if (sum == goal) return 1; // 정답을 찾은 경우
int now = 0;
now += go(count+1, sum+1, goal); // 정답을 찾지못한 경우, 다음 경우 호출
now += go(count+1, sum+2, goal); // 정답을 찾지못한 경우, 다음 경우 호출
now += go(count+1, sum+3, goal); // 정답을 찾지못한 경우, 다음 경우 호출
return now;
}goal = 4 인 경우에 재귀 호출 순서를 보면,
- 먼저, 1만 세 번 넣는 경우, now에 1+1+1+1=4이 누적되고, sum==goal이므로 출력
- 1+1+1+2 > 4 이므로 불가능, return 0
- 1+1+2 = 4 이므로 sum==goal이 되어 return 1
- 1+1+3 > 4 이므로 불가능, return 0
- 1+2+1 = 4 이므로 sum==goal이 되어 return 1
- ...
- 3+1 = 4 이므로 sum==goal이 되어 return 1 -> 정답 완성됨
- 3+1+1 > 4 이므로 불가능, return 0
- 3+1+2 > 4 이므로 불가능, return 0
- 3+1+3 > 4 이므로 불가능, return 0
- 3+2 > 4 이므로 불가능, return 0
- 3+3 > 4 이므로 불가능, return 0
- return now -> 전체 누적값 리턴
int go(int count, int sum, int goal) {
if (sum > goal) return 0; // 불가능한 경우
if (sum == goal) return 1; // 정답을 찾은 경우
int now = 0;
for (int i=1; i<=3; i++) {
now += go(count+1, sum+i, goal); // 정답을 찾지못한 경우, 다음 경우 호출
}
return now;
}의미상 count를 넣었지만, 여기에서는 sum이 탈출조건에 포함되므로, count는 사실상 필요가 없다.
int go(int sum, int goal) {
if (sum > goal) return 0; // 불가능한 경우
if (sum == goal) return 1; // 정답을 찾은 경우
int now = 0;
for (int i=1; i<=3; i++) {
now += go(sum+i, goal); // 정답을 찾지못한 경우, 다음 경우 호출
}
return now;
}재귀를 이용하여 구현한 코드
#include <iostream>
using namespace std;
int go(int sum, int goal) {
if (sum > goal) return 0; // 불가능한 경우
if (sum == goal) return 1; // 정답을 찾은 경우
int now = 0;
for (int i=1; i<=3; i++) {
now += go(sum+i, goal); // 정답을 찾지못한 경우, 다음 경우 호출
}
return now;
}
int main() {
int t;
cin >> t;
while (t--) {
int n;
cin >> n;
cout << go(0, n) << '\n'; // 0부터 n이 될 때까지 반복
}
return 0;
}2.3. 동적 프로그래밍으로 구현
DP 설계
먼저, D[n]을 찾아야 한다. 이 문제는 D[n]이 무엇인지 문제에 그대로 나와있다. 따라서 문제에 주어진 정답에 관한 설명을 그대로 옮기면 된다. 그리고 점화식을 세우기 위해서 나열을 해본다.
? + ? + ? + ... ? + ? = n 에서 마지막 부분부터 역으로 생각해보면,
[합 = n - 1] + 1 = n
[합 = n - 2] + 2 = n
[합 = n - 3] + 3 = n
이 세 가지 외에는 다른 방법이 존재하지 않는다. 따라서 이 문제는 DP로 풀이가 가능하다. 이를 그대로 점화식으로 세우면 D[n] = D[n-1] + D[n-2] + D[n-3] 이 된다.
• D[i] = i를 1, 2, 3의 합으로 나타내는 방법의 수
• D[i] = D[i-1] + D[i-2] + D[i-3]
D[0]은 점화식으로 구할 수 없는 값이다. 따라서 직접 D[0]=1로 대입한다. 이는 크기가 0인 공집합과 같다. D[1]은 ? + 1 = 1, ? + 2 = 1, ? + 3 = 1 중에 2와 3의 경우 음수가 되므로 불가능하다. 따라서 이에 대한 예외처리도 해 주어야 한다.
DP로 풀이한 코드
#include <stdio.h>
int d[11];
int main() {
d[0] = 1;
for (int i=1; i<=10; i++) {
if (i-1 >= 0) {
d[i] += d[i-1];
}
if (i-2 >= 0) {
d[i] += d[i-2];
}
if (i-3 >= 0) {
d[i] += d[i-3];
}
}
int t;
scanf("%d",&t);
while (t--) {
int n;
scanf("%d",&n);
printf("%d\n",d[n]);
}
}