깊이 우선 탐색(DFS)

트리의 순회와 같이 그래프의 모든 정점들을 특정한 순서에 따라 방문하느 알고리즘을 그래프의 탐색(search) 알고리즘이라고 한다. 트리와는 달리, 그래프에서는 탐색 과정에서 얻어지는 정보가 매우 중요하다. 탐색 과정에서 어떤 간선이 사용되었는지, 또 어떤 순서로 정점들이 방문되었는지를 통해 그래프의 구조를 알 수도 있다. 예를 들어, 미로 찾기를 한다면 길이 있는 곳에 대해서만 연결된 간선을 방문해가면서 도착지점까지 탐색해볼 수 있을것이다. 그렇게 도착지점까지 도달하면 그동안 방문한 노드가 미로의 탐색경로가 된다.

탐색 알고리즘 중에서 가장 많이 사용되는 것이 깊이 우선 탐색(depth-first search, DFS) 와 너비 우선 탐색(breadth-first search, BFS) 이다. DFS는 모든 정점을 방문하는 가장 단순하고 고전적인 방법이다. 현재 정점과 인접한 간선들을 하나씩 검사하다가, 아직 방문하지 않은 정점으로 향하는 간선이 있다면 그 간선을 무조건 방문한다. 이 과정에서 더 이상 방문할 곳이 없다면, 마지막에 방문했던 간선을 따라 뒤로 돌아간다.

여기서 '마지막에' 방문했던 곳으로 돌아간다는 것이 익숙한 표현이다. 바로 스택(Stack) 자료구조의 동작방식과 유사하다. 따라서 DFS는 스택을 통해 구현할 수 있다. 스택을 이용하여 간선 정보를 Push하면서 방문하다가 더이상 방문할 노드가 없다면 Pop하면서 다시 방문할 노드를 탐색해가면 될 것이다. 대부분의 언어에서는 재귀함수가 내부적으로는 스택으로 구현되어있으므로, DFS의 구현은 재귀함수의 형태로 많이 구현된다.

1. DFS 동작원리

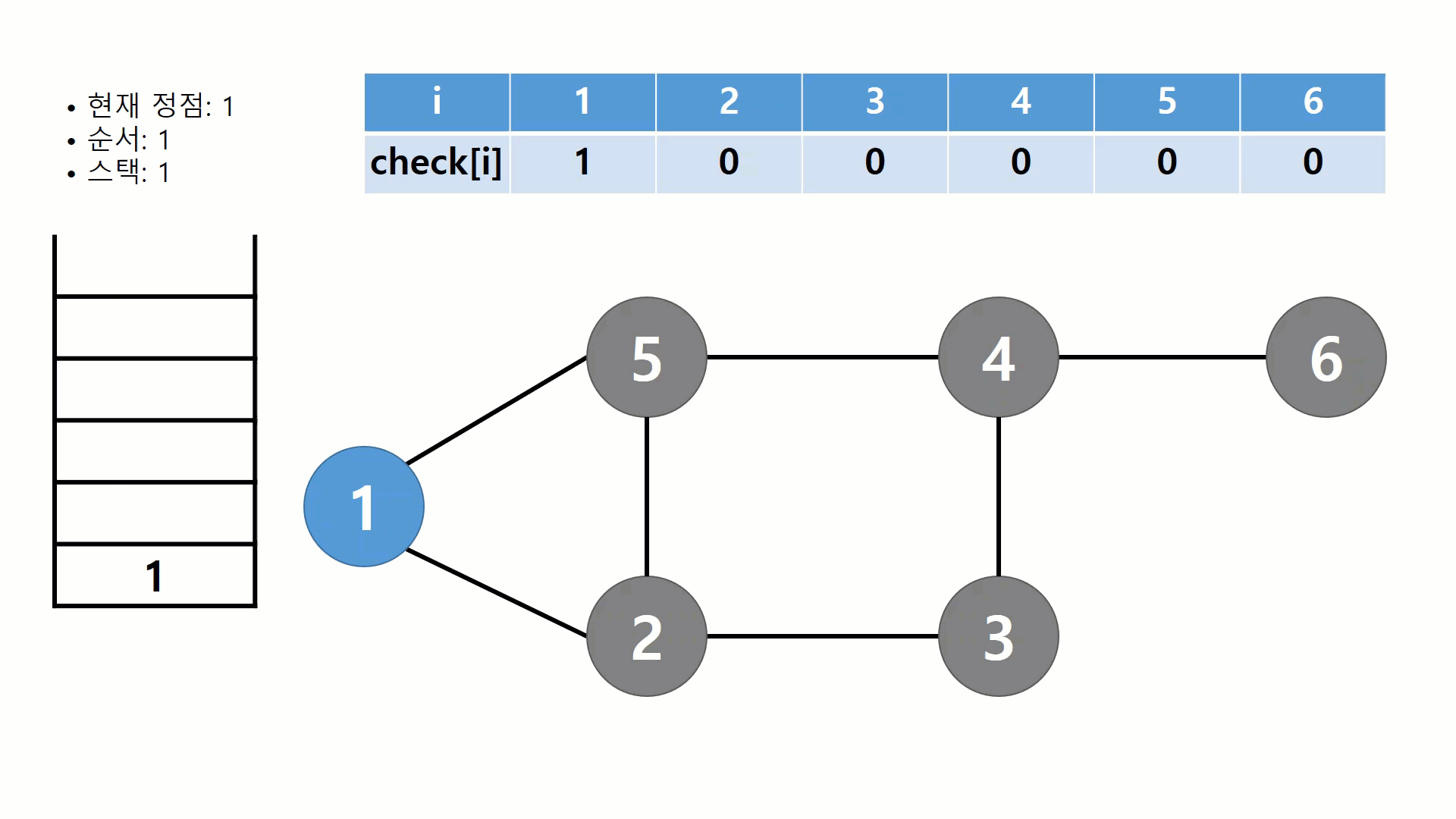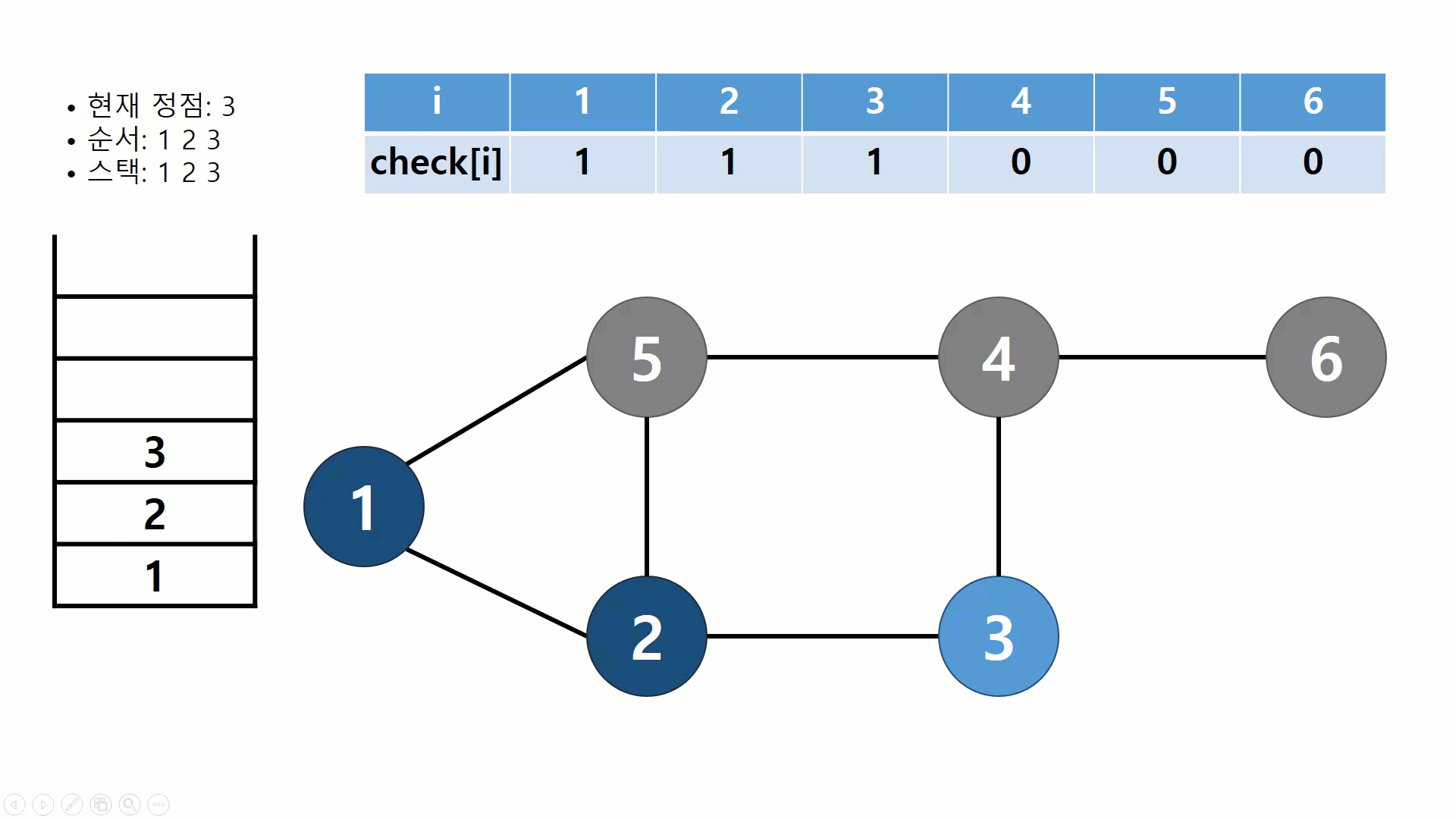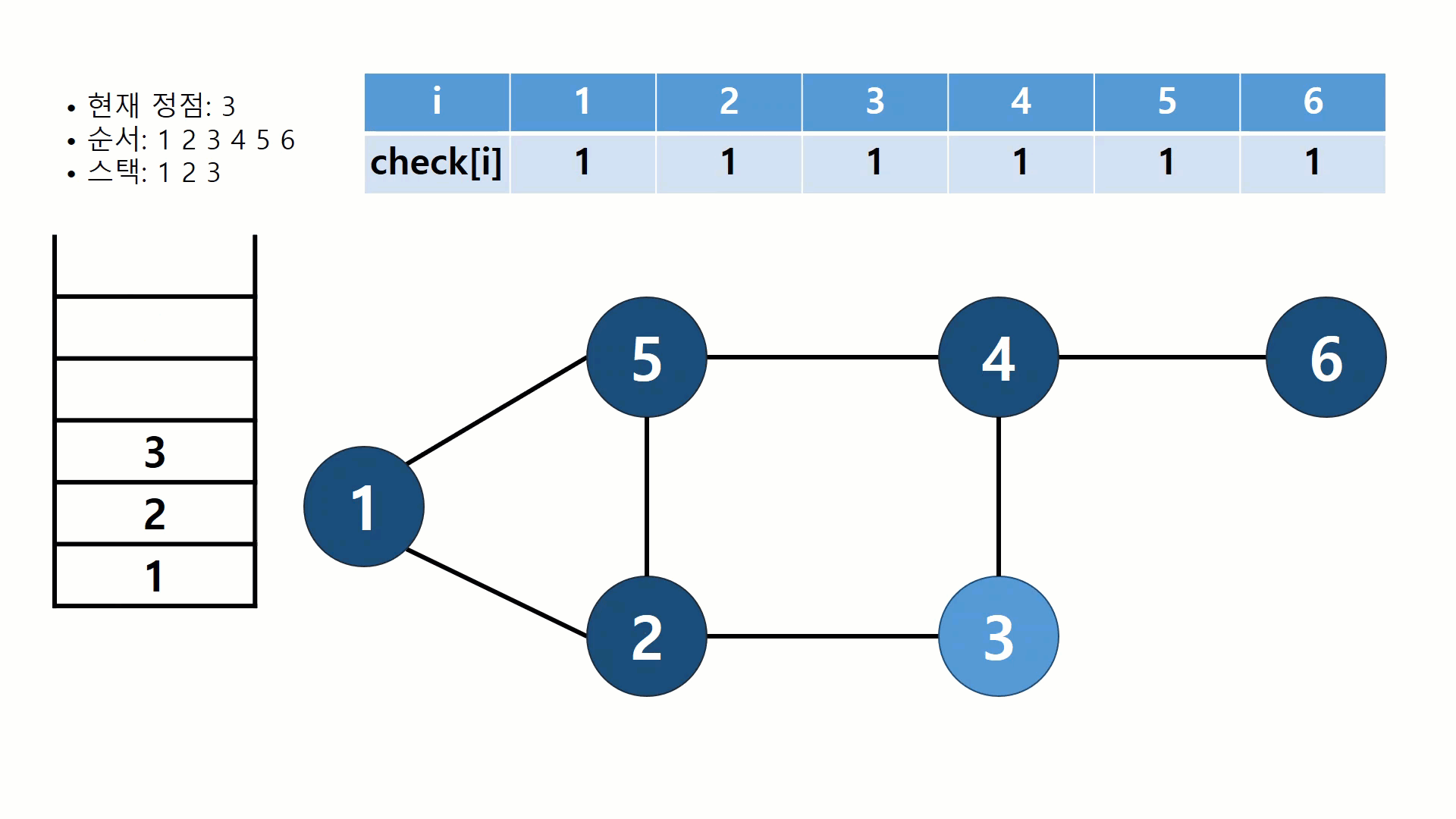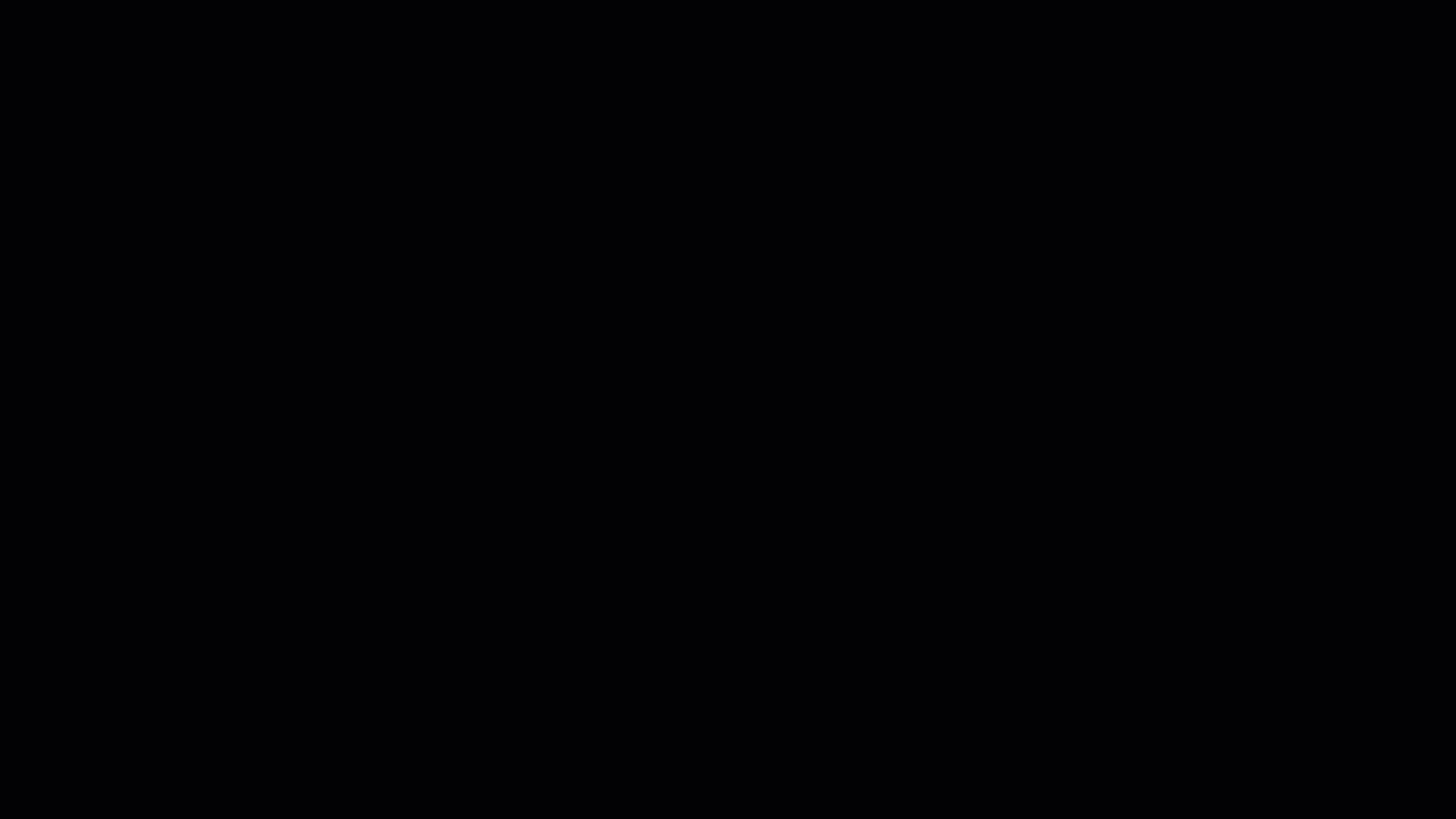
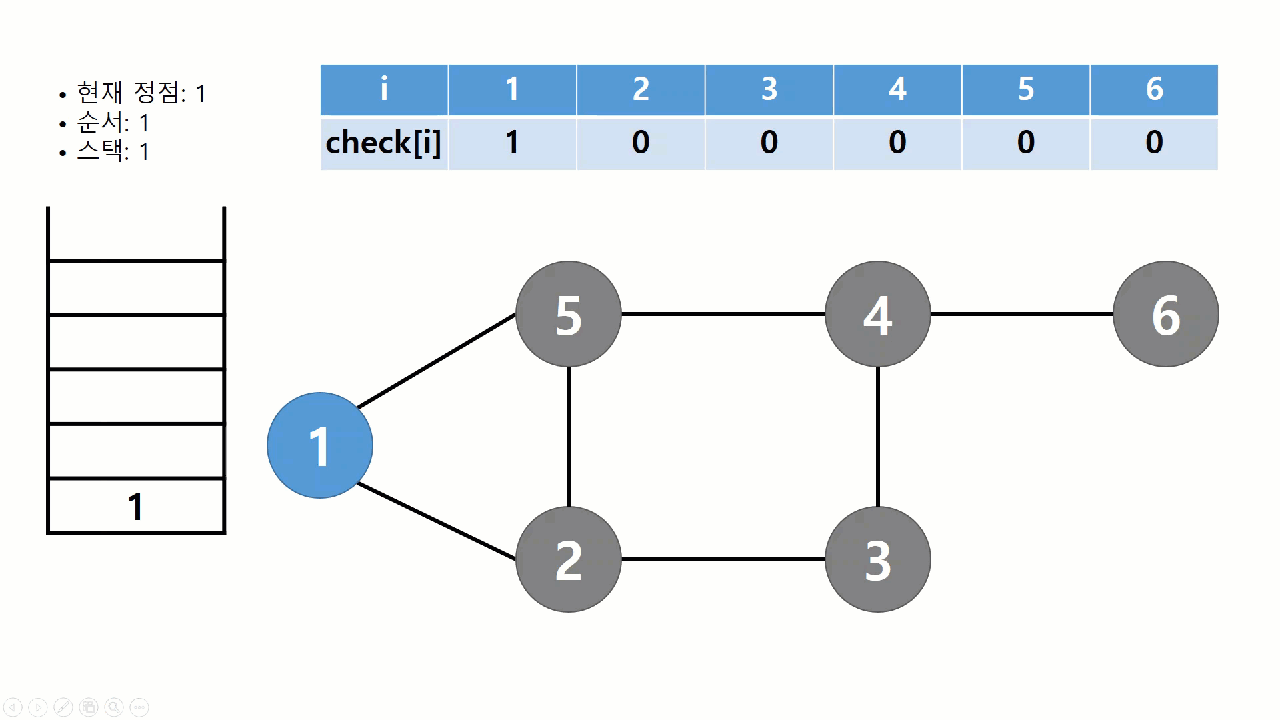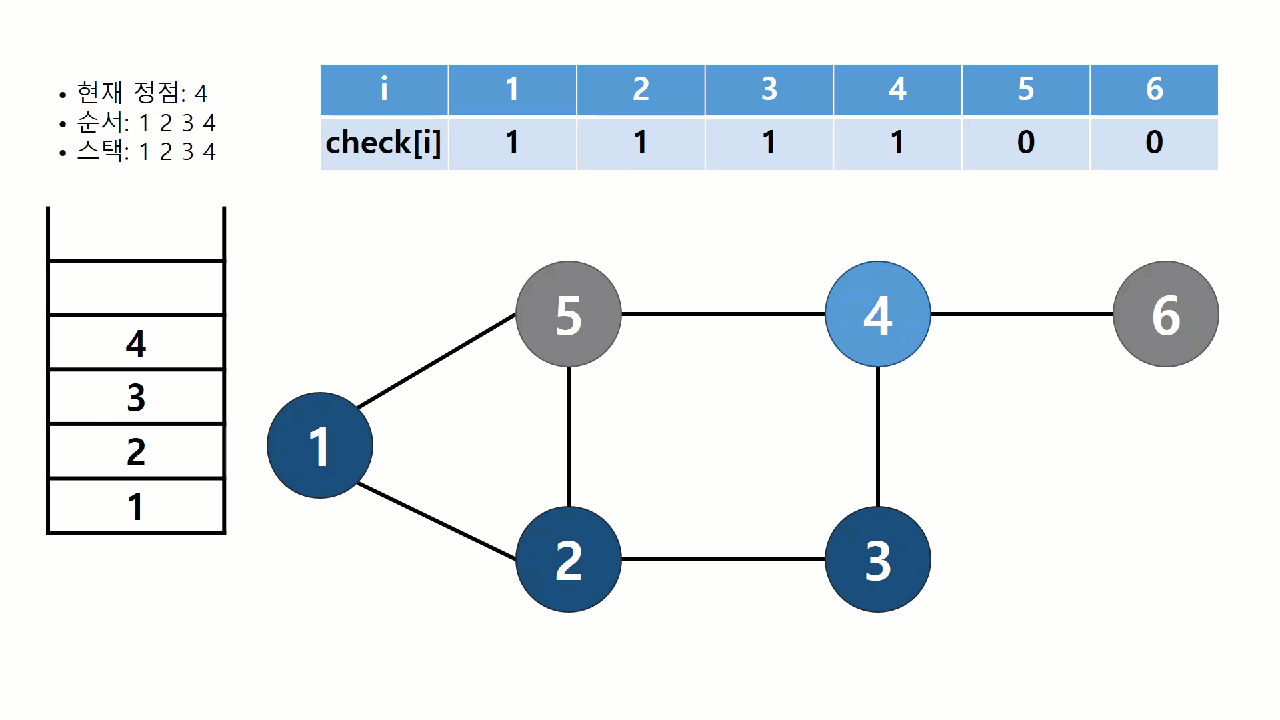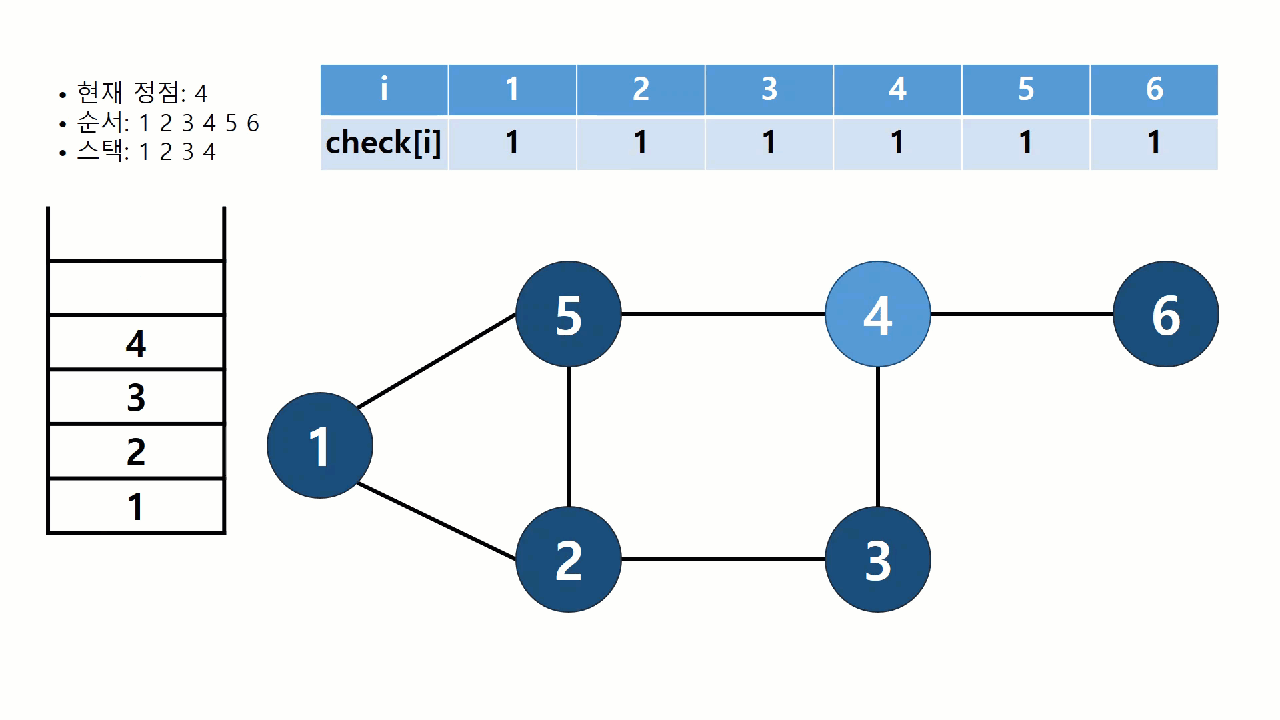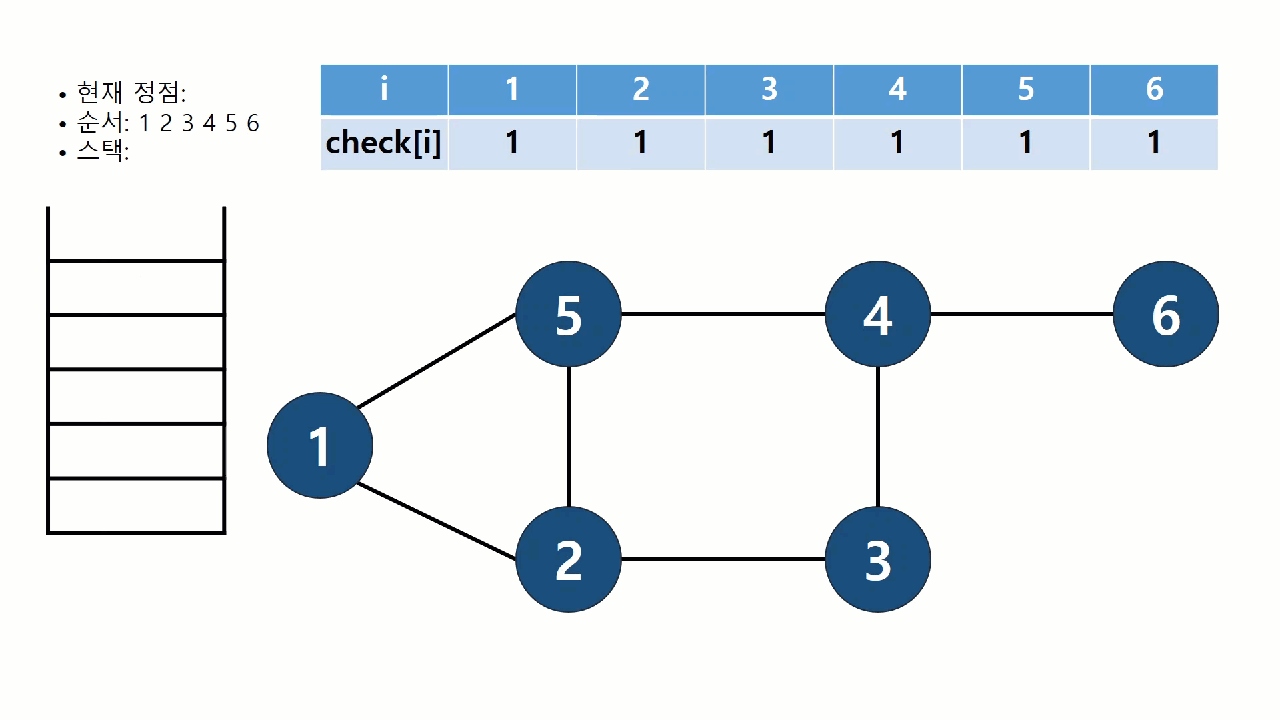
위 그림은 1번 정점에서 시작해서 숫자가 작은 정점부터 차례대로 방문하는 DFS의 동작방식을 보여준다. 방문 여부를 표시하기 위해서 check배열을 두고, 스택에 지나온 정점을 Push하면서 나아간다. 1번 정점부터 DFS가 진행되는 과정을 나열하면 다음과 같다.

• 1번 정점을 방문하고, 스택에 1을 넣고, check배열의 1번 값을 1로 바꾼다.
• 2번 정점을 방문하고, 스택에 2를 넣고, check배열으 2번 값을 1로 바꾼다. (숫자가 작은것부터)
• 3번 정점을 방문하고, 스택에 3을 넣고, check배열의 3번 값을 1로 바꾼다.
• 4번 정점을 방문하고, 스택에 4을 넣고, check배열의 4번 값을 1로 바꾼다.
• 5번 정점을 방문하고, 스택에 5을 넣고, check배열의 5번 값을 1로 바꾼다.
• 5번 정점에서 더이상 방문할 곳이 없으므로, 스택에서 5를 꺼내고, 4번 정점으로 돌아간다.
• 6번 정점을 방문하고, 스택에 6을 넣고, check배열의 6번 값을 1로 바꾼다.
• 6번 정점에서 더이상 방문할 곳이 없으므로, 스택에서 6을 꺼내고, 4번 정점으로 돌아간다.
• 4번 정점에서 더이상 방문할 곳이 없으므로, 스택에서 4을 꺼내고, 3번 정점으로 돌아간다.
• 3번 정점에서 더이상 방문할 곳이 없으므로, 스택에서 3을 꺼내고, 2번 정점으로 돌아간다.
• 2번 정점에서 더이상 방문할 곳이 없으므로, 스택에서 2을 꺼내고, 1번 정점으로 돌아간다.
• 1번 정점에서 더이상 방문할 곳이 없으므로, 스택에서 1을 꺼내고, 탐색이 끝난다.

---

2. DFS 구현

인접 행렬을 이용한 DFS 구현

인접 행렬에 그래프가 저장되어 있다면, 다음과 같이 DFS를 구현할 수 있다. 이때 주의할 점은 a[x][i]의 값이 1인지(연결된 간선이 있는지) 확인하면서 방문한적이 없는 정점을 방문해야 한다는 것이다.

void dfs(int x) {
  check[x] = true;
  for (int i=1; i<=n; i++) {
    if (a[x][i] == 1 && check[i] == false) { // 연결여부와 방문여부 확인
    	dfs(i);
    }
  }
}

인접 리스트를 이용한 DFS 구현

인접 리스트에 그래프가 저장되어 있다면, 다음과 같이 DFS를 구현할 수 있다. 이때는 인접 행렬을 이용한 DFS구현과 달리, 연결된 간선을 확인할 필요가 없이 방문여부만 확인하면 된다. 왜냐하면 인접 리스트에는 이미 연결된 간선만 저장되어 있을 것이기 때문이다.

void dfs(int x) {
  check[x] = true;
  for (int i=0; i<a[x].size(); i++) {
    int y = a[x][i];
    if (check[y] == false) { // 방문여부만 확인
    	dfs(y);
    }
  }
}

---

3. DFS를 활용한 문제풀이

BOJ 1260. DFS와 BFS

• 문제링크 : https://www.acmicpc.net/problem/1260

그래프를 DFS로 탐색한 결과와 BFS로 탐색한 결과를 출력하는 프로그램을 작성하시오. 단, 방문할 수 있는 정점이 여러 개인 경우에는 정점 번호가 작은 것을 먼저 방문하고, 더 이상 방문할 수 있는 점이 없는 경우 종료한다. 정점 번호는 1번부터 N번까지이다.

인접 리스트 기반의 구현

#include <cstdio>
#include <algorithm>
#include <cstring>
#include <vector>
#include <queue>
using namespace std;

vector<int> a[1001];	// 인접 리스트
bool check[1001];	// 방문 여부 저장

void dfs(int node) {
    check[node] = true;	// 방문 표시
    printf("%d ",node);	// 방문(출력)
    for (int i=0; i<a[node].size(); i++) { // 각 노드에 연결된 간선을 탐색
        int next = a[node][i];
        if (check[next] == false) {	// 방문 하지 않았다면 탐색
            dfs(next);
        }
    }
}
void bfs(int start) {
    ...
}
int main() {
    int n, m, start;	// 정점의 개수, 간선의 개수, 탐색 시작점
    scanf("%d %d %d",&n,&m,&start);
    for (int i=0; i<m; i++) {
        int u,v;
        scanf("%d %d",&u,&v);
        a[u].push_back(v);	// 양방향 그래프이므로
        a[v].push_back(u);	// 양쪽에 연결
    }
    for (int i=1; i<=n; i++) {	// 각 인접 리스트 요소를 오름차순 정렬
        sort(a[i].begin(), a[i].end());
    }
    dfs(start); puts("");
    bfs(start); puts("");
    return 0;
}

비재귀 구현(스택 라이브러리 사용)

#include <cstdio>
#include <stack>
#include <algorithm>
#include <cstring>
#include <vector>
#include <queue>
using namespace std;

vector<int> a[1001];	// 인접 리스트
bool check[1001];	// 방문 여부 저장

void dfs(int node) {
    stack<pair<int,int>> s;	// 스택 정의 <노드번호, 연결된 노드번호>
    s.push(make_pair(node,0));
    check[node] = true;
    printf("%d ",node);
    while (!s.empty()) {
        int node = s.top().first;
        int start = s.top().second;
        s.pop();
        for (int i=start; i<a[node].size(); i++) { // 인접 리스트의 각 요소를 탐색
            int next = a[node][i];
            if (check[next] == false) {
                printf("%d ",next);
                check[next] = true;
                s.push(make_pair(node,i+1));
                s.push(make_pair(next,0));
                break;
            }
        }
    }
}
void bfs(int start) {
    ...
}
int main() {
    ...
}