알고리즘

스택(Stack) 자료구조 스택은 흔히 프링글스에 비유가 된다. 프링글스 통 안에 감자칩이 쌓여있지만 우리는 가장 위에 있는 감자칩부터 꺼내는 수 밖에 없다. 즉, 마지막으로 넣은 것이 (맨위에 있으므로) 가장 먼저 나오는 Last In First Out(LIFO) 구

브루트 포스는 모든 경우의 수를 다 해보는 것이다. 실제로 사람이 모든 케이스를 일일이 계산해보는 것은 바람직한 방법은 아니다. 그리고 그렇게 하다보면 실수를 하기 마련이다. 마치 고등학교 때 수능시험에서의 노가다 와 같다. 하지만 전산학에서는 엄연히 하나의 알고리즘으

그래프(Graph)는 현실 세계의 사물이나 추상적인 개념 간의 연결 관계를 표현하는 자료구조이다. 여러 도시들을 연결하는 도로망, 사람들 간의 관계, 웹 사이트 간의 링크 관계 등이 그러한 연결 구조이다. 그래프는 계층 구조인 트리와는 다르게 부모 자식 관계에 관한 제

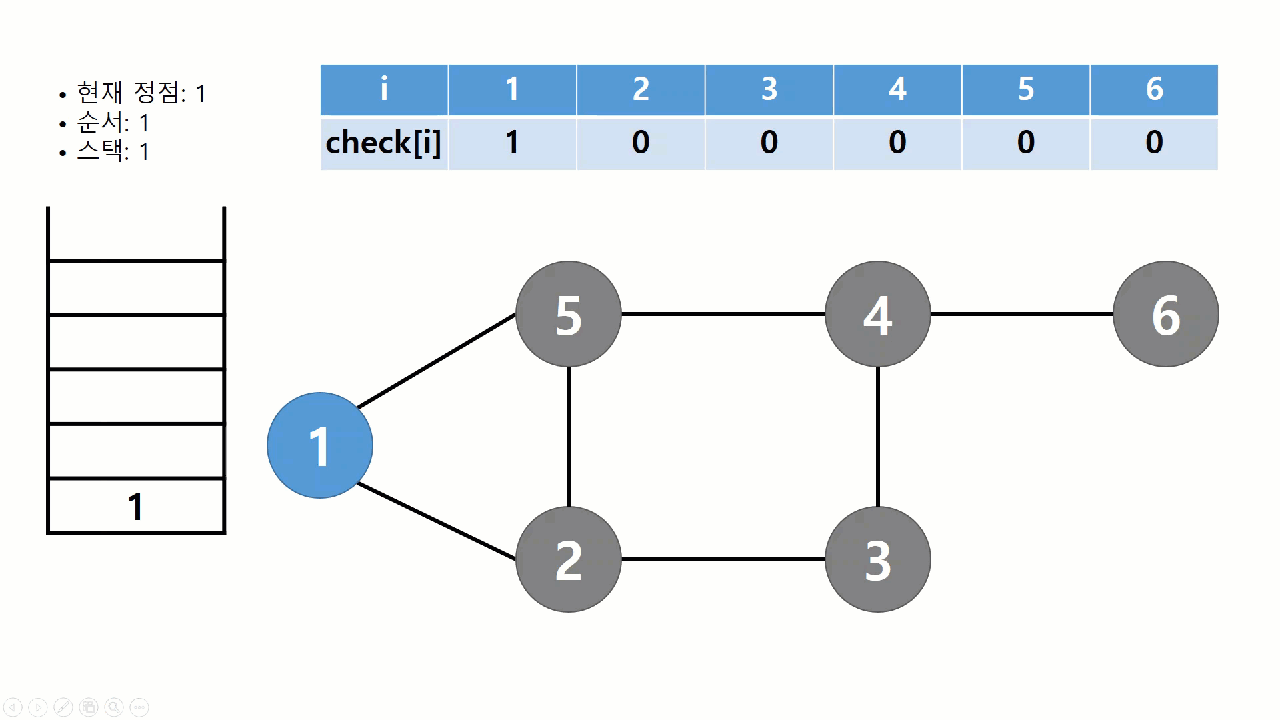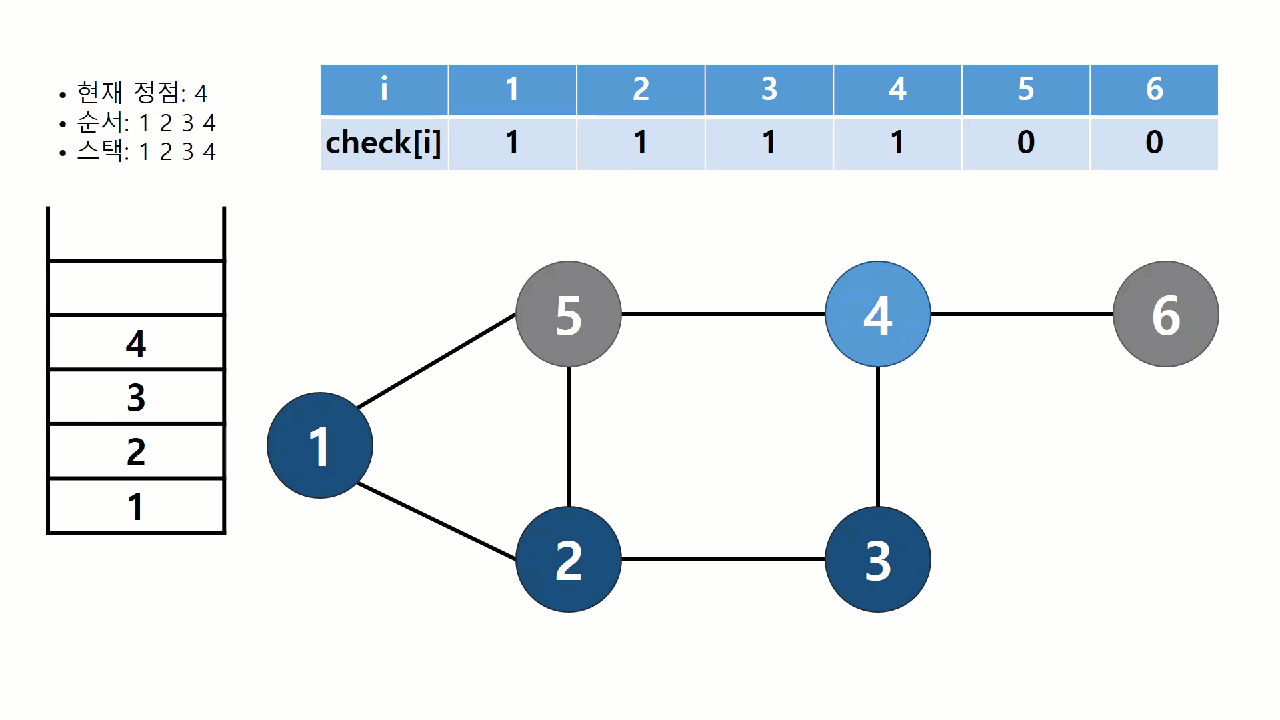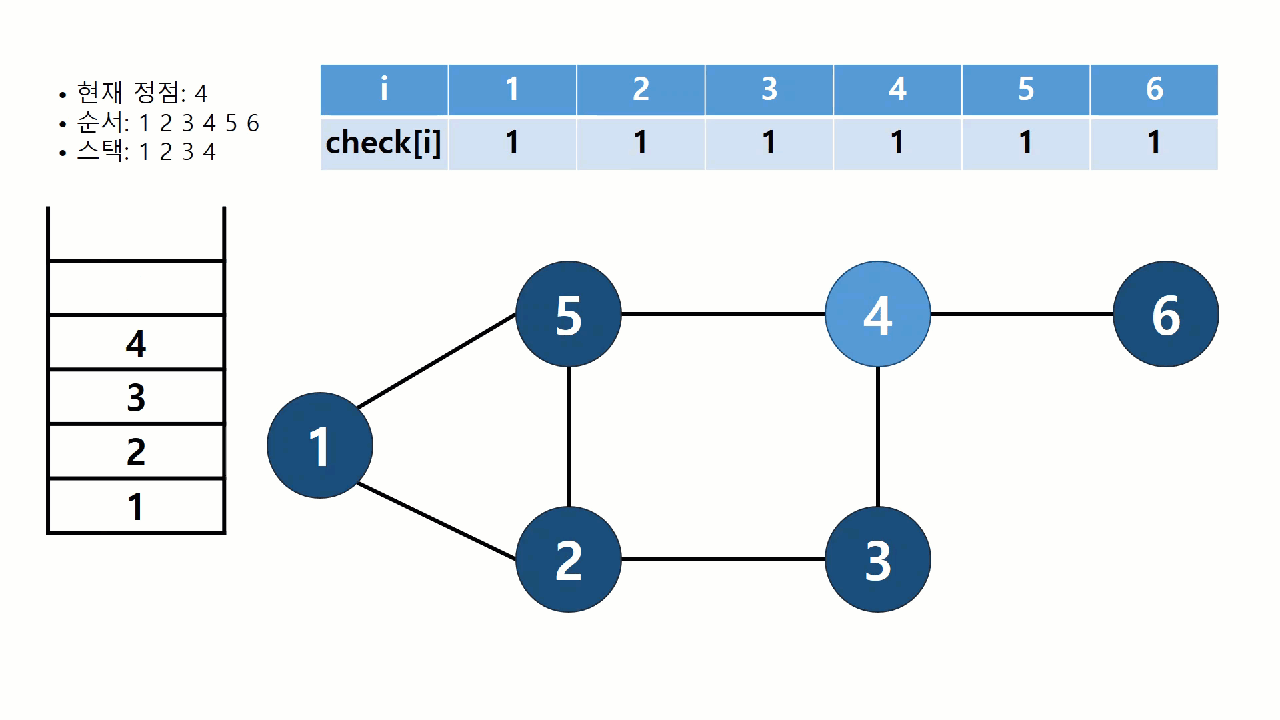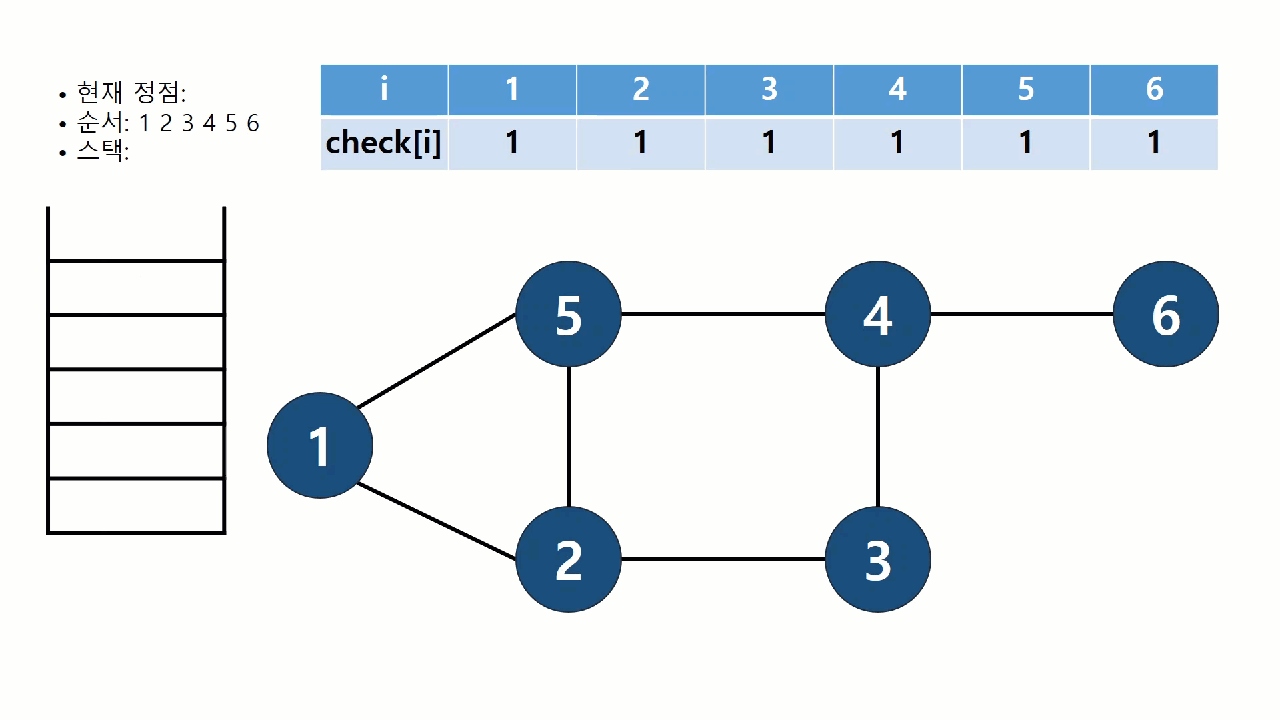
트리의 순회와 같이 그래프의 모든 정점들을 특정한 순서에 따라 방문하느 알고리즘을 그래프의 탐색(search) 알고리즘이라고 한다. 트리와는 달리, 그래프에서는 탐색 과정에서 얻어지는 정보가 매우 중요하다. 탐색 과정에서 어떤 간선이 사용되었는지, 또 어떤 순서로 정점

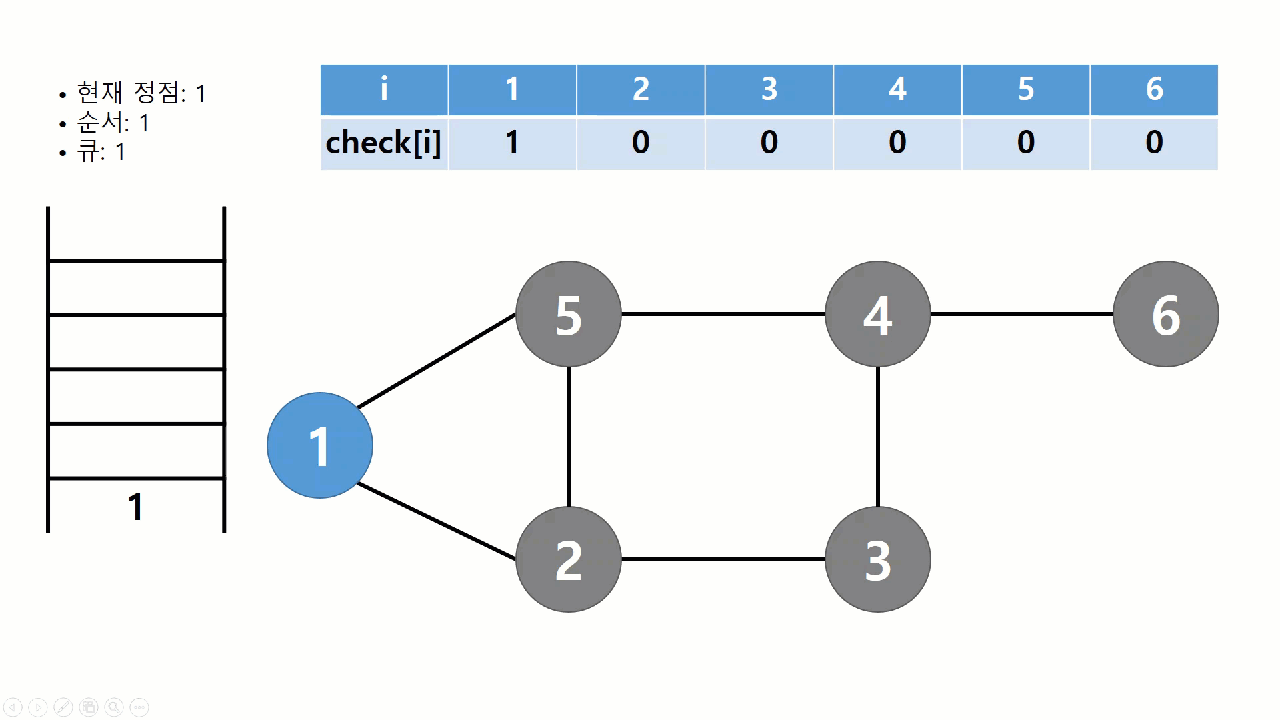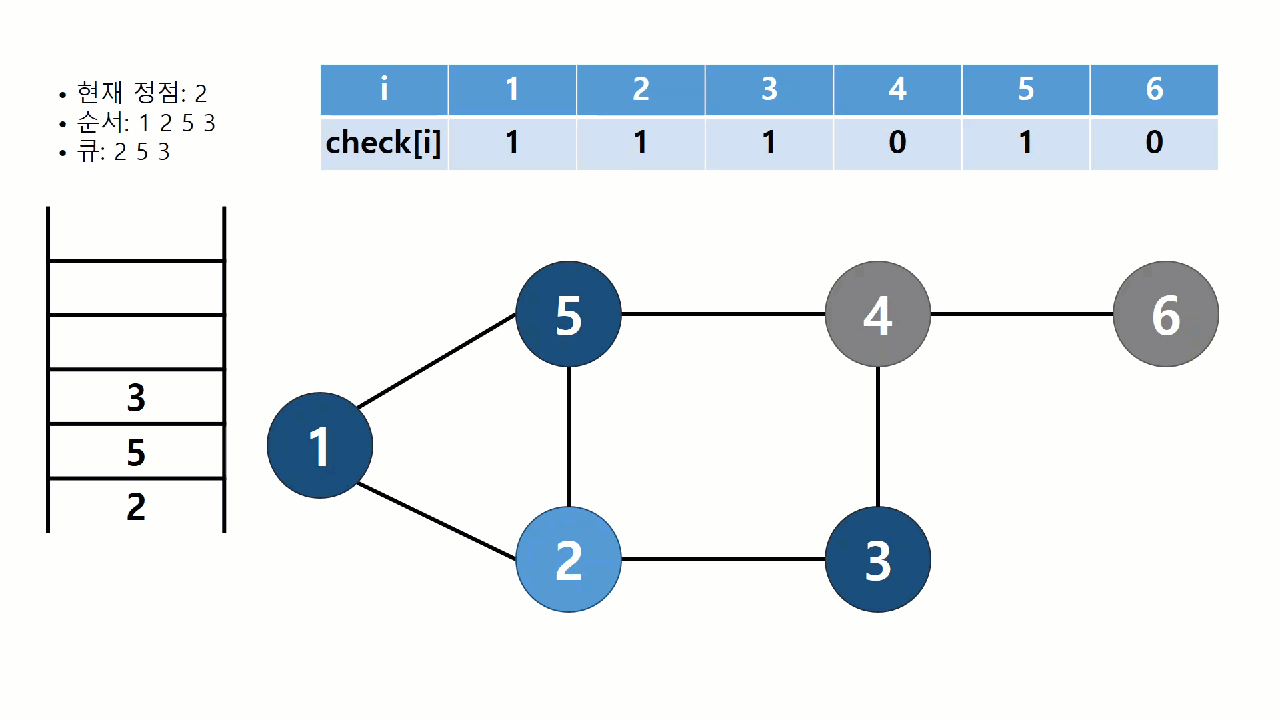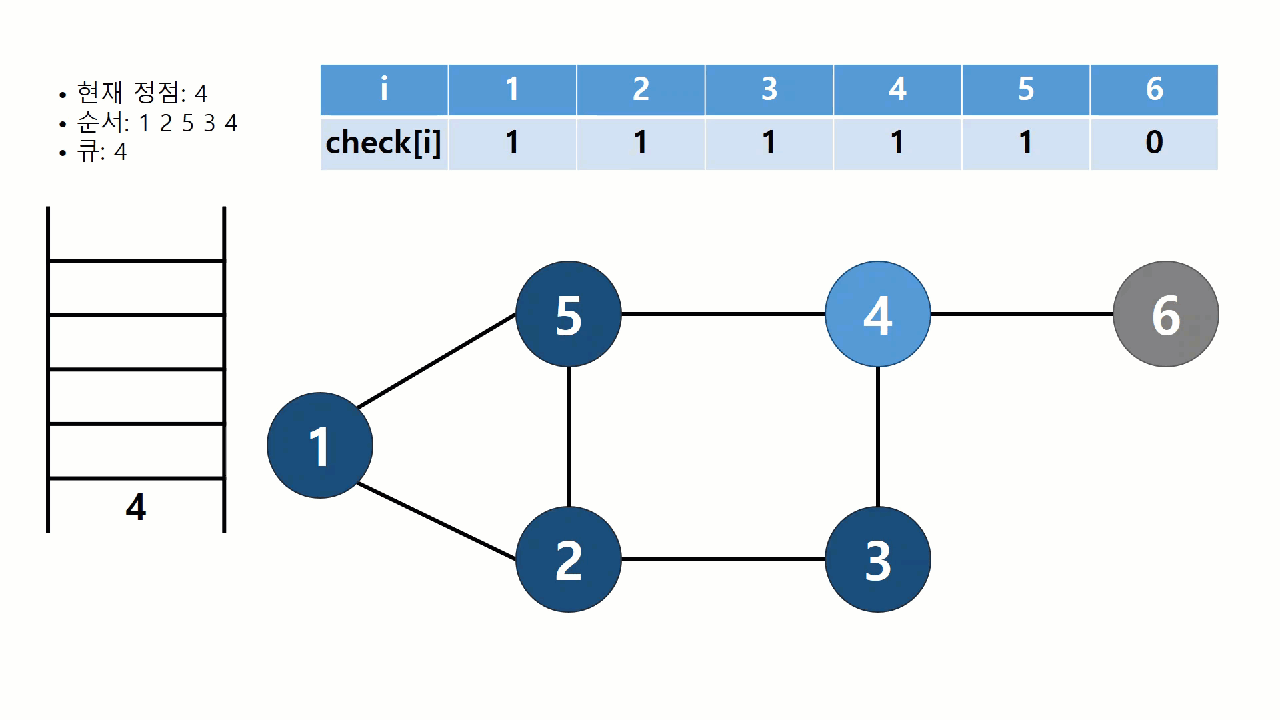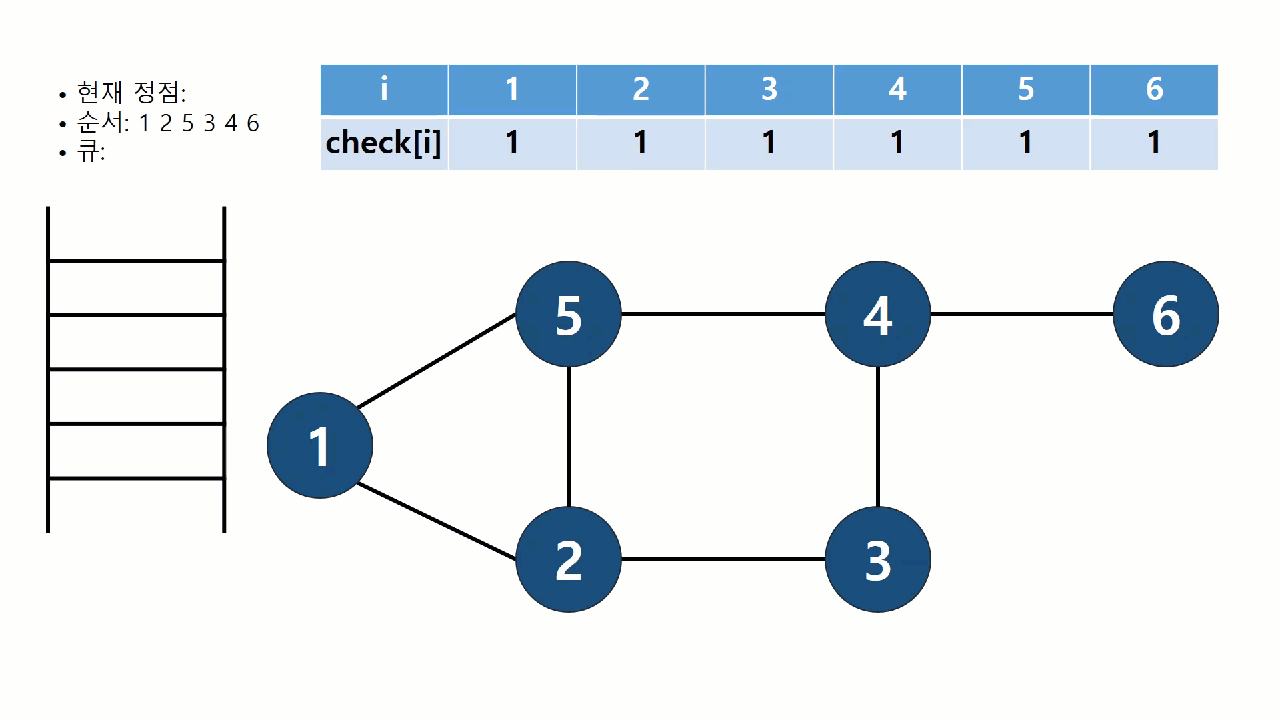
너비 우선 탐색(breadth-first search, BFS)는 시작점에서 가까운 정점부터 순서대로 방문하는 탐색 알고리즘이다. 가까운 정점을 모두 저장해놓고 순서대로 방문해야 하므로, 스택 구조로는 구현이 어렵다. 따라서 큐(Queue) 자료구조를 사용한다. BFS

그래프 중에서는 위 그림과 같이 여러 개로 나누어져 있을 수도 있다. 위 그림을 보고 두 개의 그래프라고 볼 수도 있지만, 하나의 그래프에 두 개의 연결 요소를 가진다고 볼 수도 있다. 그 이유는 정점 사이에 겹치는 것이 없기 때문이다. 연결 요소로 본다면, 나누어진

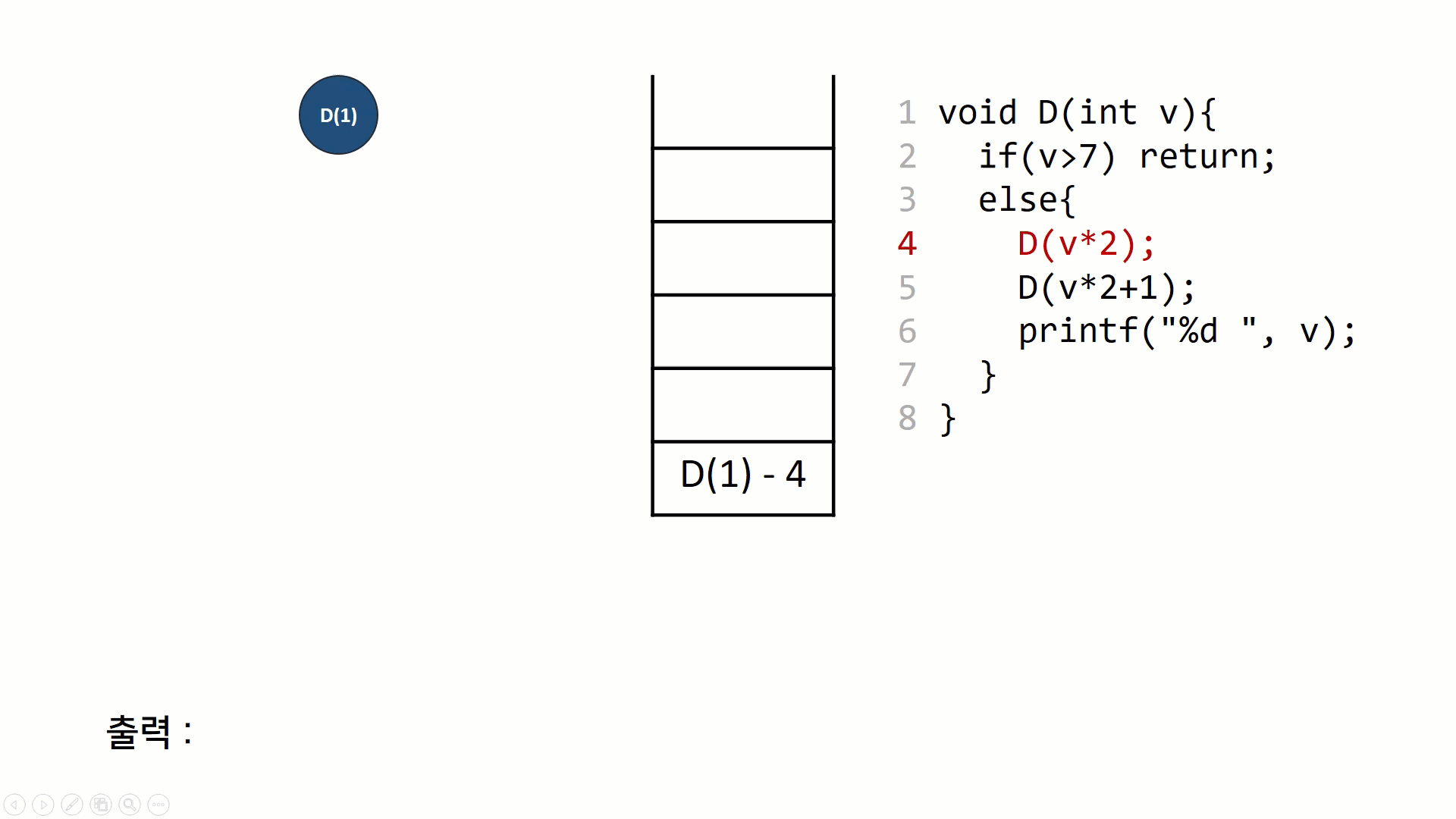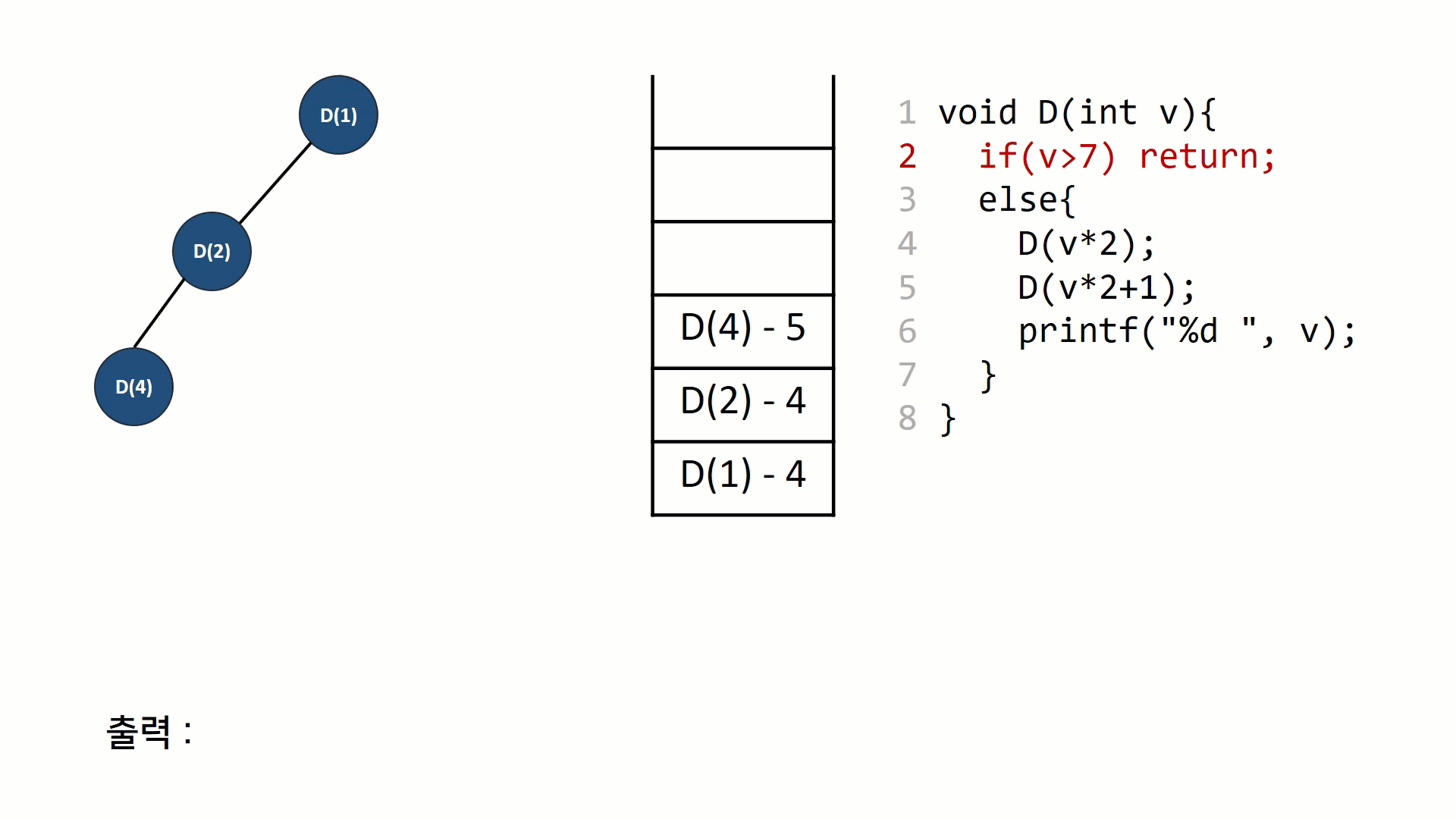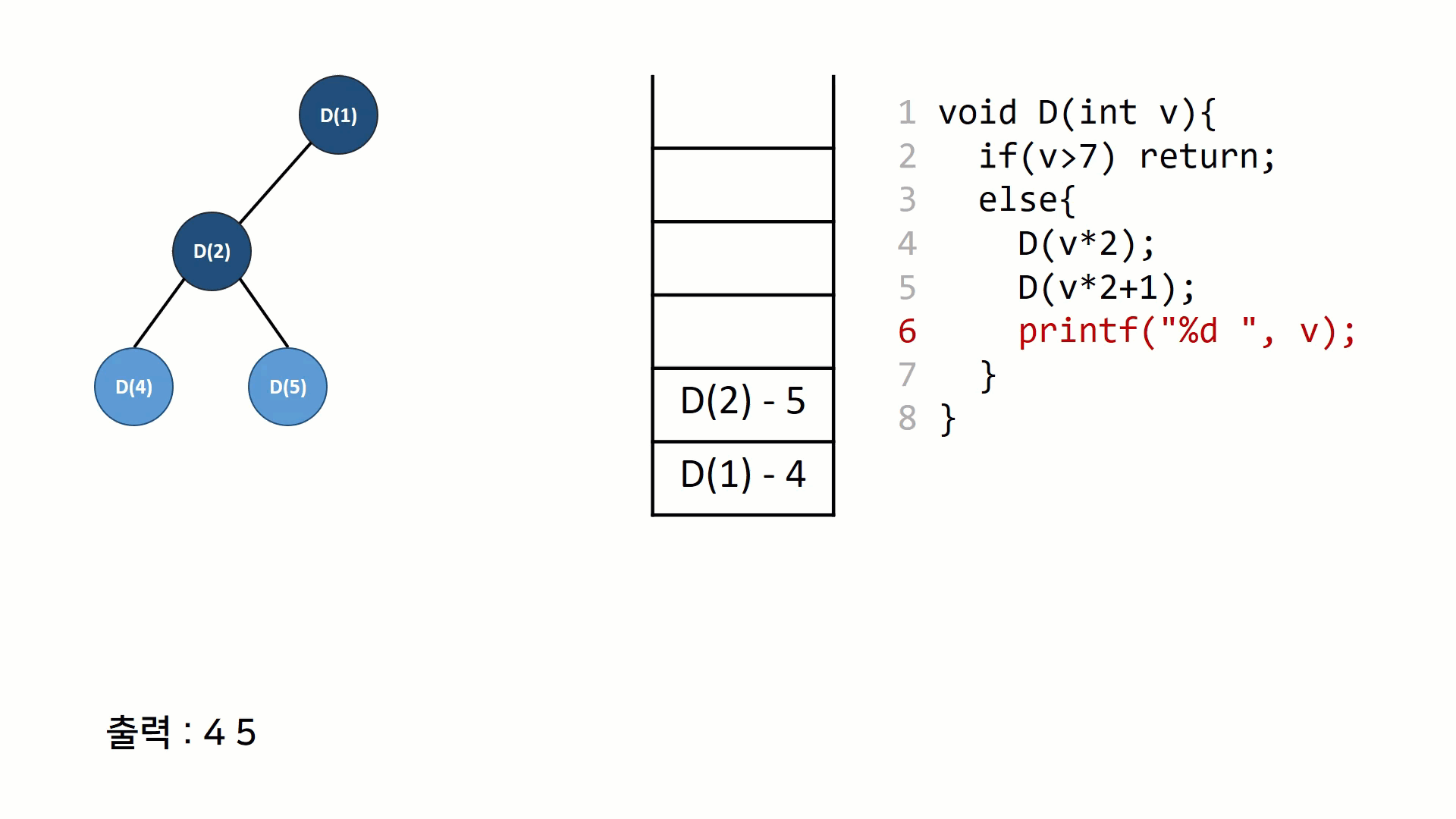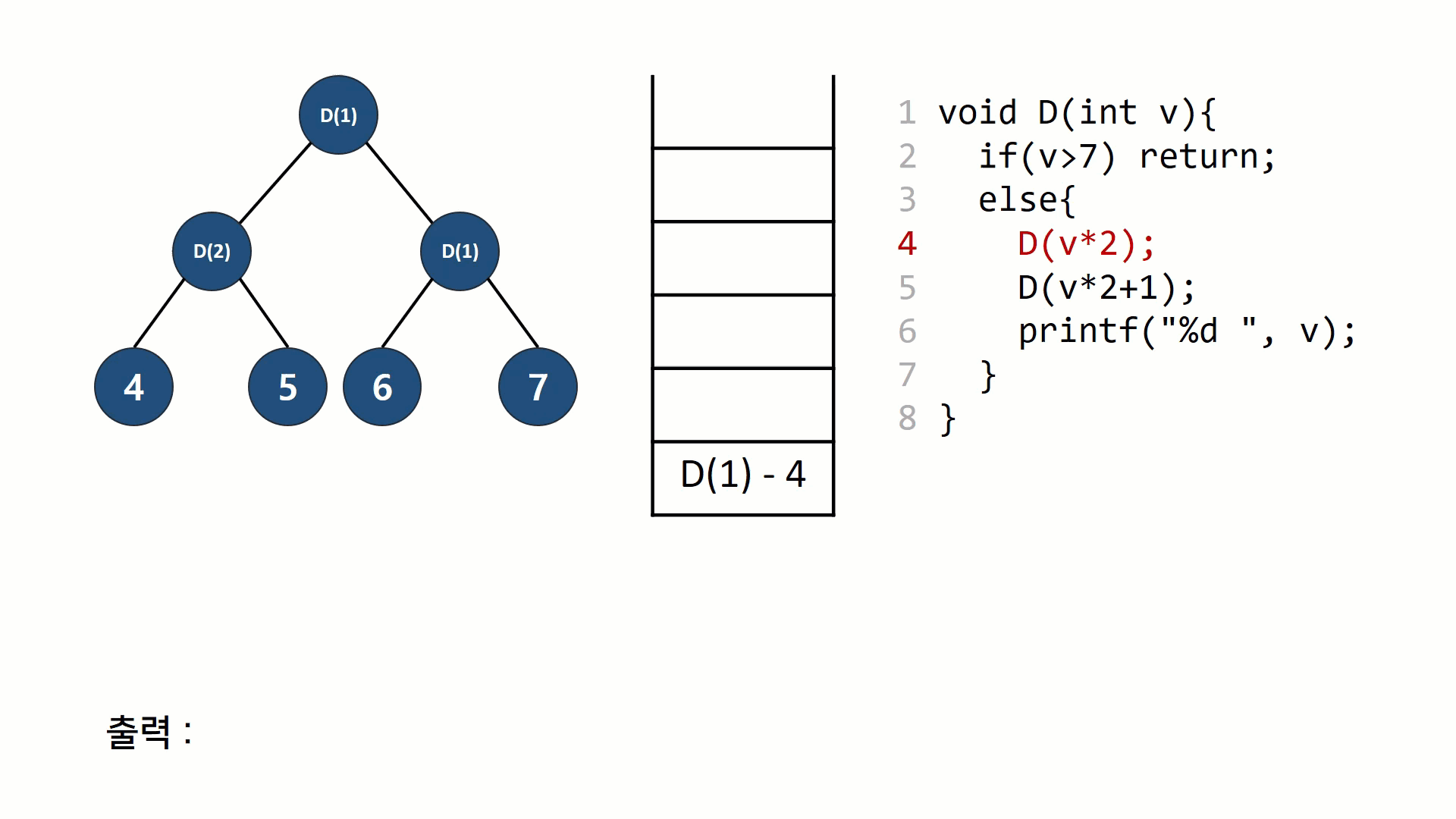
가능한 방법을 전부 만들어 보는 알고리즘 들을 가리켜 '완전 탐색(exhaustive search)' 라고 부른다. 손으로 직접 풀기에는 경우의 수가 너무 많은 경우, 완전 탐색은 (컴퓨터의 처리속도를 이용하여)충분히 빠르면서도 구현하기 쉬운 대안이 된다.간단한 예로,

동적 계획법(Dynamic Programming, DP)은 큰 문제를 작은 문제로 나누어서 푸는 방식의 알고리즘이다. 동적 계획법은 처음 주어진 문제를 더 작은 문제들로 나눈 뒤 각 조각의 답을 계산하고, 이 답들로부터 원래 문제에 대한 답을 계산해 낸다는 점에서 분할

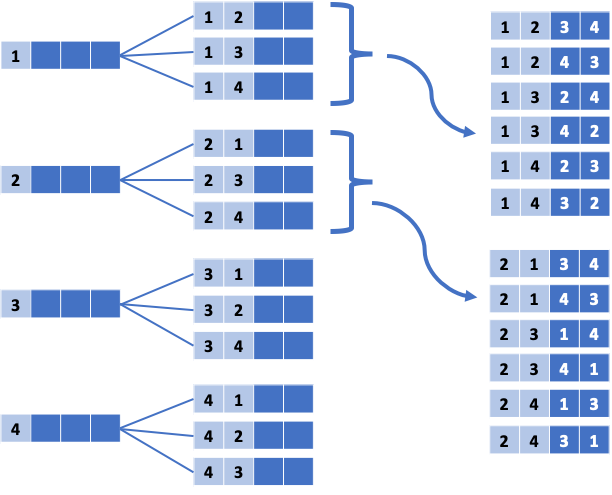
순열은 임의의 수열을 서로 다른 순서로 섞는 것이다. 순열은 브루트 포스 문제를 풀어야 하는데 순서가 매우 중요한 의미를 가질 때 사용할 수 있다. 예를 들어, 123과 132가 서도 다른 의미를 가지는 경우가 그렇다. N개의 수에 대한 순열을 사전순으로 나열하면 총

알고리즘의 성능을 평가하는 요소는 크게 두 가지가 있다. 첫 번째는 어떤 알고리즘이 어떠한 상황에서 더 빠르냐?이고 두 번째는 어떤 알고리즘이 어떠한 상황에서 메모리를 더 많이 쓰냐?이다. 전자는 속도에 관한 것이고 후자는 메모리 사용량에 관한 것이다. 이에 해당하는