재귀(Recursion)

가능한 방법을 전부 만들어 보는 알고리즘 들을 가리켜 '완전 탐색(exhaustive search)' 라고 부른다. 손으로 직접 풀기에는 경우의 수가 너무 많은 경우, 완전 탐색은 (컴퓨터의 처리속도를 이용하여)충분히 빠르면서도 구현하기 쉬운 대안이 된다.

간단한 예로, 열 명의 학생을 한 줄로 세우려고 하는데, 특정한 두 명을 인접하지 않도록 세우는 방법을 찾으려고 한다. 이 문제를 풀 수 있는 가장 쉬운 방법은 일단 열 명의 학생들을 줄 세우는 모든 경우를 만들어 보고, 각 경우에 두 명의 학생이 인접한지 확인하는 것이다. 이때 경우의 수는 360만 가지나 되지만, 컴퓨터는 1초안에 결과를 낼 수 있다.

1. 재귀 호출의 목적

재귀 함수란, 자신이 수행할 작업을 유사한 형태의 여러 조각으로 쪼갠 뒤, 그중 한 조각을 수행하고, 나머지를 자기 자신을 호출함으로써 실행하는 함수이다.

약간은 어려운 말이지만, 코드로 보면 오히려 이해가 빠르다. 다음은 n을 입력 받아 1부터 n까지의 합을 반환하는 함수이다.

반복문으로 구현

int sum(int n){
    int ret = 0;
    for(int i = 1; i <= n ; ++i)
        ret+=i;
    return ret;
}

재귀함수로 구현

int recursiveSum(int n){
    if(n == 1) return 1; // 더이상 쪼개지지 않을 때, 기저 사례(base case)
    return n + recursiveSum(n+1);
}

if문을 보면 '더이상 쪼개지지 않는' 최소한의 작업에 도달했을 때 종료하면서 답을 반환한다. 이때 쪼개지지 않는 가장 작은 작업들을 가리켜 재귀 호출의 기저 사례(base case)라고 한다.

중첩 반복문을 대체

0번부터 n번 까지의 원소 중 네 개를 고르는 모든 경우를 출력하라는 문제가 있다. 이 경우 for문으로 구현하려면 4중 for문으로 구현해야한다.

반복문으로 구현

for(int i=0; i<n; ++i)
  for(int j=i+1; j<n; ++j)
    for(int k=j+1; k<n; ++k)
      for(int l=k+1; l<n; ++l)
        cout << i << " " << j << " " << k << " " << l << endl;

위 코드 조각이 하는 작업은 네 개의 조각으로 나눌 수 있다. 각 조각에서 하나의 원소를 고르는 것이다. 이렇게 원소를 고른 뒤, 남은 원소들을 고르는 작업을 자기 자신을 호출해 떠넘기는 재귀 함수를 구현할 수가 있다. 이때 남은 원소들을 고르는 '작업'을 다음과 같은 입력들의 집합으로 정의할 수 있다.

• 원소들의 총 개수 : n
• 지금까지 고른 원소들의 번호 : picked
• 더 골라야 할 원소들의 개수 : toPick

void pick(int n, vector<int>& picked, int toPick){
  if(toPick == 0) { // 기저 사례: 더 고를 원소가 없을 때 고른 원소들을 출력
    printPicked(picked);
    return;
  }
  int smallest = picked.empty() ? 0 : picked.back() + 1;
  for(int next=smallest; next<n; ++next){
    picked.push_back(next);
    pick(n, picked, toPick - 1);
    picked.pop_back();
  }
}

위 코드의 경우 n이 아무리 커져도 코드가 그대로 유지된다. 반면에 for 반복문을 사용할 경우에는 for문이 n만큼 중첩되어야 할 것이다. 이것만 보아도 재귀호출의 의의는 충분하다. 그리고 더 나아가 DFS, DP 등 여러가지 알고리즘에서 재귀 호출을 응용할 수 있다.

---

2. 재귀 함수 분석

재귀 함수는 내부적으로 스택을 사용한다는 점을 잊어서는 안된다. 다시 한번 단계별로 재귀 함수를 구성하는 과정에 대해 살펴보자. 간단한 예로, 1부터 3까지 출력하는 재귀 함수를 구현해본다.

void recur(int x){
	printf("%d ", x);
    recur(x-1);
}

이 함수를 실행하면 무한루프를 돌게 될 것이다. 왜냐하면 기저 사례를 처리하는 부분이 없기 때문이다.(종료 조건이 없기 때문이다.) 따라서 가장 작은 작업 단위가 되면 값을 반환하고 종료하는 조건문이 추가되어야 할 것이다.

void recur(int x){
	if(x>0){
    	printf("%d ", x);
        recur(x-1);
    }
}

이렇게 if문에서 0보다 큰 경우에만 실행하도록 하면, x가 0보다 작아졌을 때 종료를 하게된다. 가장 바람직한 구조는 탈출 조건문과 반복 실행되는 부분을 분리하는 것이다.

void recur(int x){	// A code
	if(x==0) return;	// 탈출 조건문 (base case)
    else{
    	printf("%d ", x);
        recur(x-1);	// line k
    }
}

이제 위 코드가 어떻게 동작하며 실행될지 생각해보아야 한다. 그대로 실행하면 3 2 1 순으로 출력이 될 것이다. 이는 '실행해야할 일'을 재귀호출 이전에 했기 때문이다. 스택에 push하기전에 출력을 하는것이다. 1 2 3 순으로 출력을 하기 위해서는 스택에서 pop하고 나서 출력을 해야한다. 따라서 재귀호출문 바로 다음에 실행해야할 일을 넣으면 된다. 곧바로 이해가 되면 다행이지만, 그렇지 않다면 스택구조를 떠올리면 된다.

void recur(int x){	// B code
	if(x==0) return;	// 탈출 조건문 (base case)
    else{    	
        recur(x-1);	// line k
        printf("%d ", x);
    }
}

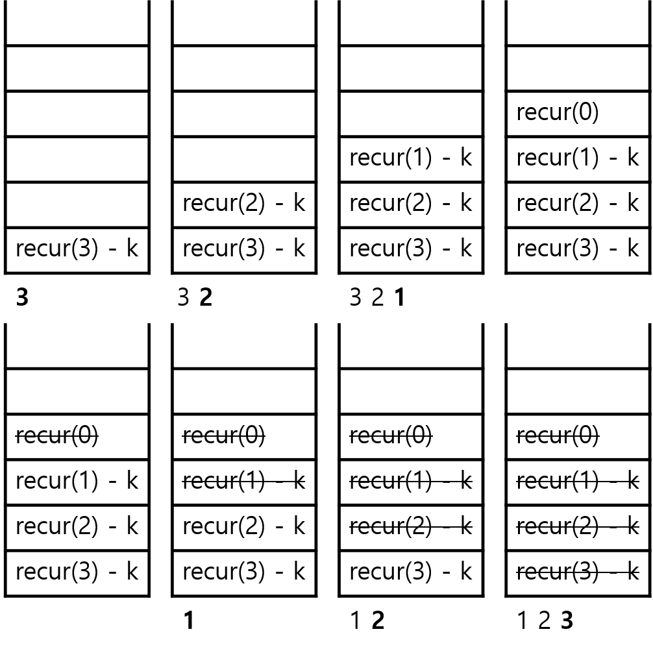
재귀 함수를 호출하는 부분이 k번째 줄이라고 하면, 내부적으로 스택에 쌓이고 빠지는 과정은 다음과 같다.

• A code는 3출력, recur(3)의 k번째 줄까지 실행했다는 것을 스택에 저장
• A code는 2출력, recur(2)의 k번째 줄까지 실행했다는 것을 스택에 저장
• A code는 1출력, recur(1)의 k번째 줄까지 실행했다는 것을 스택에 저장
• recur(0)을 스택에 저장, 탈출 조건문에 의해 리턴
• recur(1)이 스택에서 나옴, B code는 1출력
• recur(2)이 스택에서 나옴, B code는 2출력
• recur(3)이 스택에서 나옴, B code는 3출력

---

3. DFS 분석(재귀의 관점)

그래프에서의 DFS를 생각하기 이전에 이진트리에서 DFS를 생각하면 직관적으로 이해가 된다. 이진트리에서의 세 가지 순회를 재귀 호출과 스택의 관점에서 분석 해보았다.

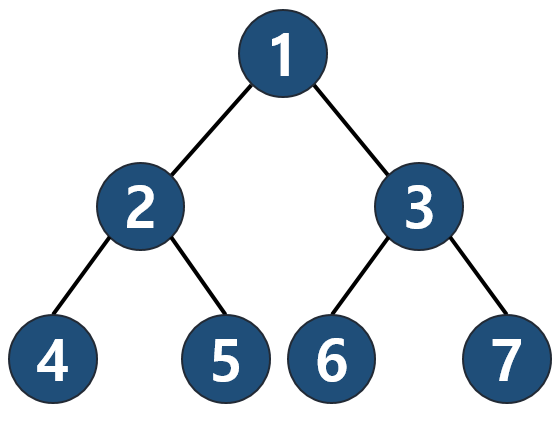
• 전위순회 출력 : 1 2 4 5 3 6 7
• 중위순회 출력 : 4 2 5 1 6 3 7
• 후위순회 출력 : 4 5 2 6 7 3 1

트리가 구현되어 있다고 가정하고, 코드 상에서는 왼쪽 서브 트리는 1 2 4 ... 로 v*2로 반복한다. 오른쪽 서브 트리는 1 3 7 ... 이므로 v*2+1로 반복한다.

#include <stdio.h>
using namespace std;

void D(int v){
  if(v>7) return;
  else{
    D(v*2);		// 왼쪽 서브 트리 탐색
    D(v*2+1);		// 오른쪽 서브 트리 탐색    
  }
}
int main() {
  D(1);
  return 0;
}

이렇게 코드를 구현하면 이진트리를 순회하는 것과 같이 동작을 한다. 하지만 실제로 호출만 될뿐 출력하는 등의 일을 하고 있지는 않다. 이 '해야할 일'을 앞쪽에 넣으면 전위순회가 되고, 중간에 넣으면 중위순회, 마지막에 넣으면 후위순회가 된다. 참고로, 후위순회는 병합정렬에서도 유용하게 사용된다.

printf("%d ", v); // 할일을 맨 앞에 두면 전위순회
D(v*2);		
D(v*2+1);

D(v*2);		
printf("%d ", v); // 할일을 가운데에 두면 중위순회
D(v*2+1);

printf("%d ", v); // 할일을 맨 둬에 두면 후위순회
D(v*2);		
D(v*2+1);

재귀호출 과정

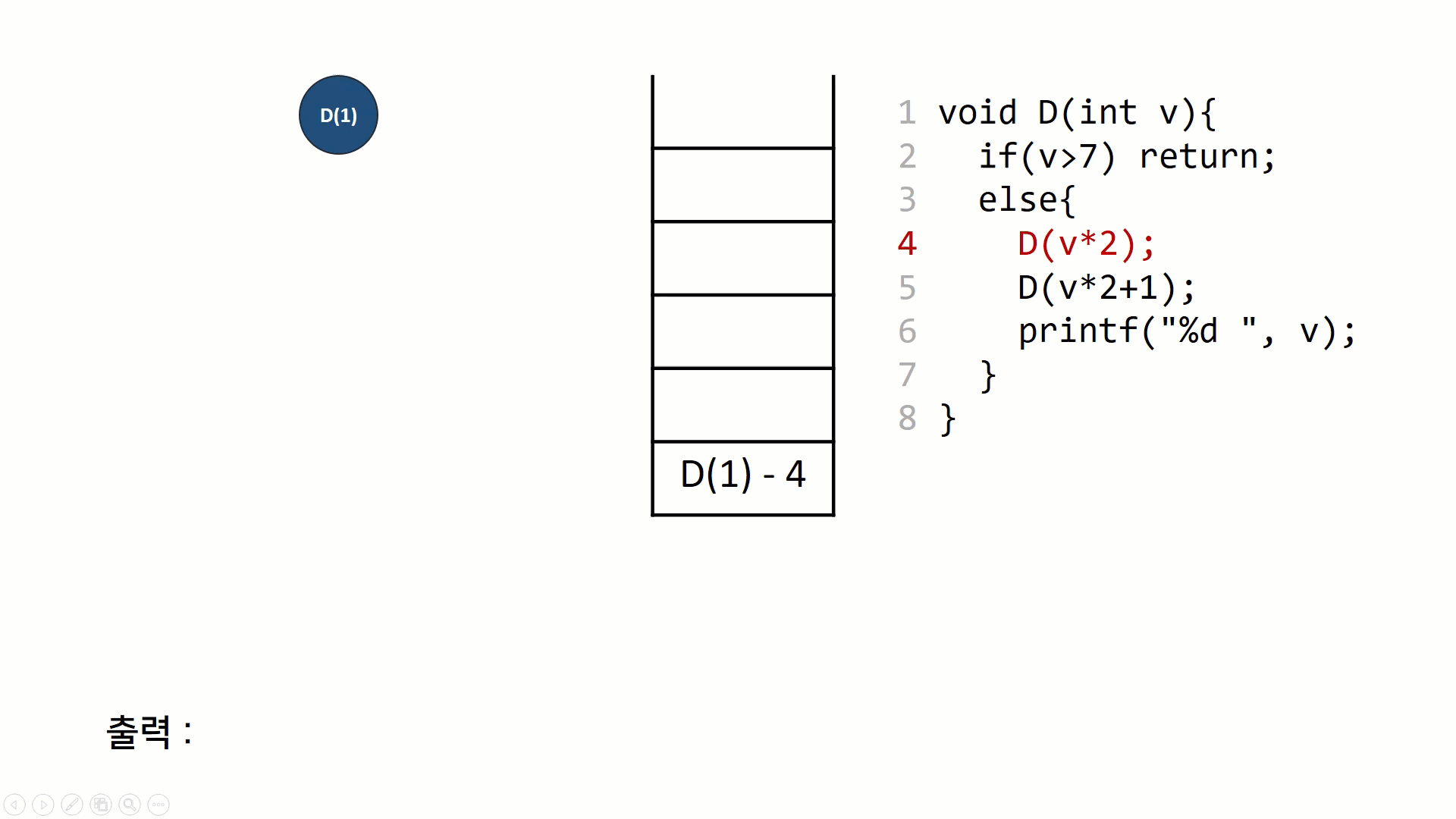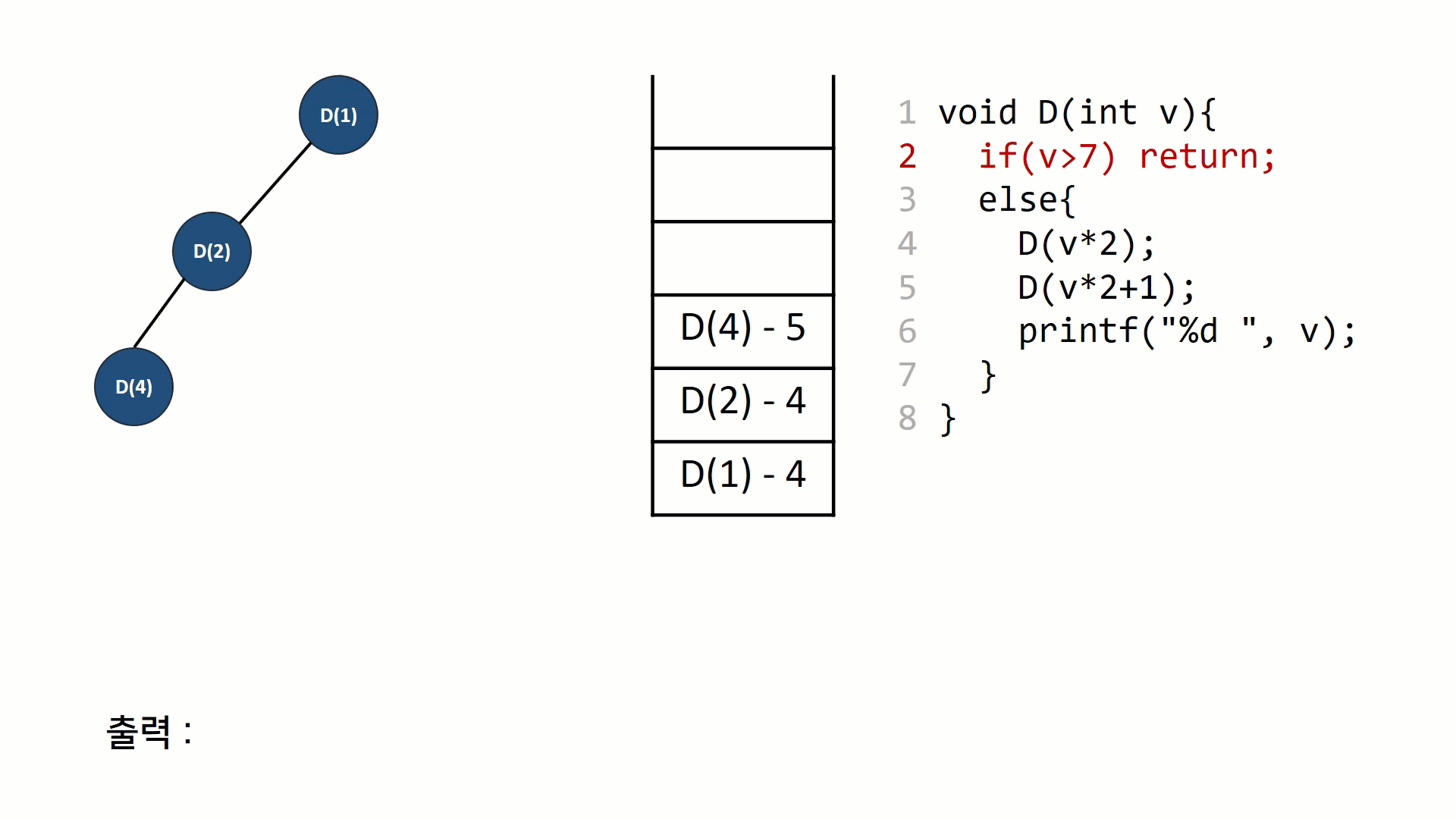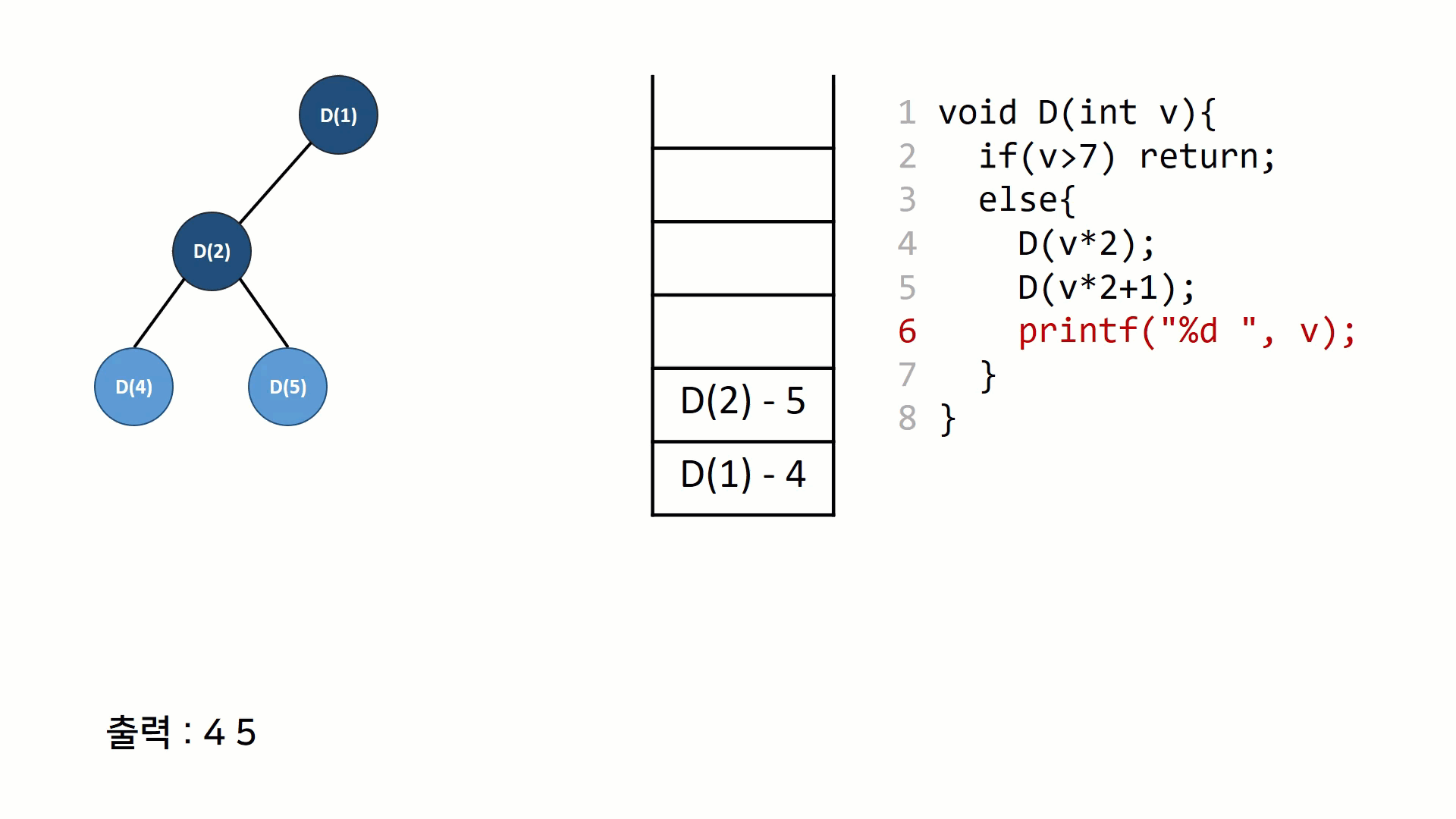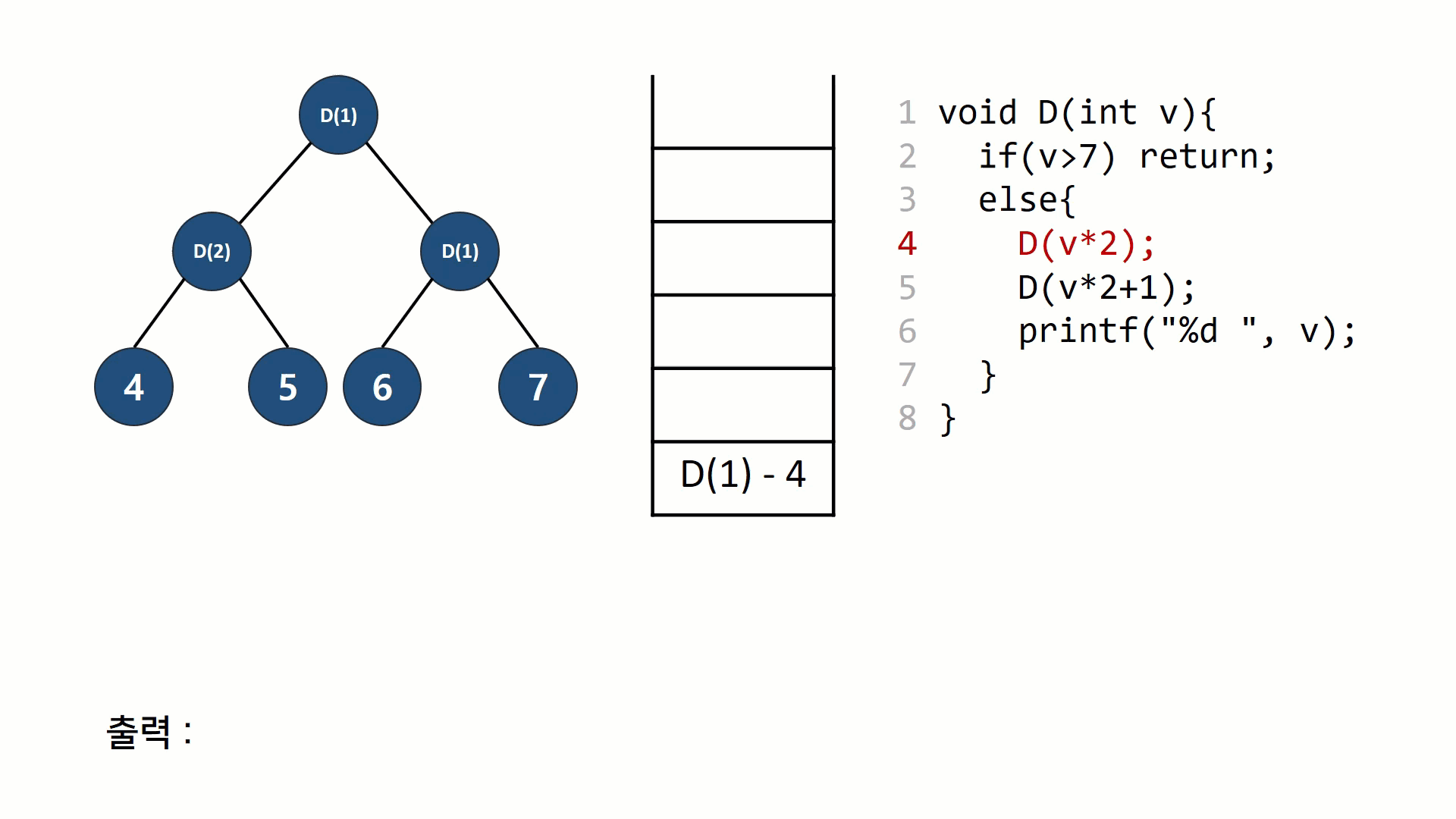
재귀호출 자체를 트리노드처럼 표현해볼 수 있다. 스택과 트리를 그려가면서 그 과정을 이해해보면 재귀호출의 동작원리가 보다 익숙하게 느껴질 수 있다.

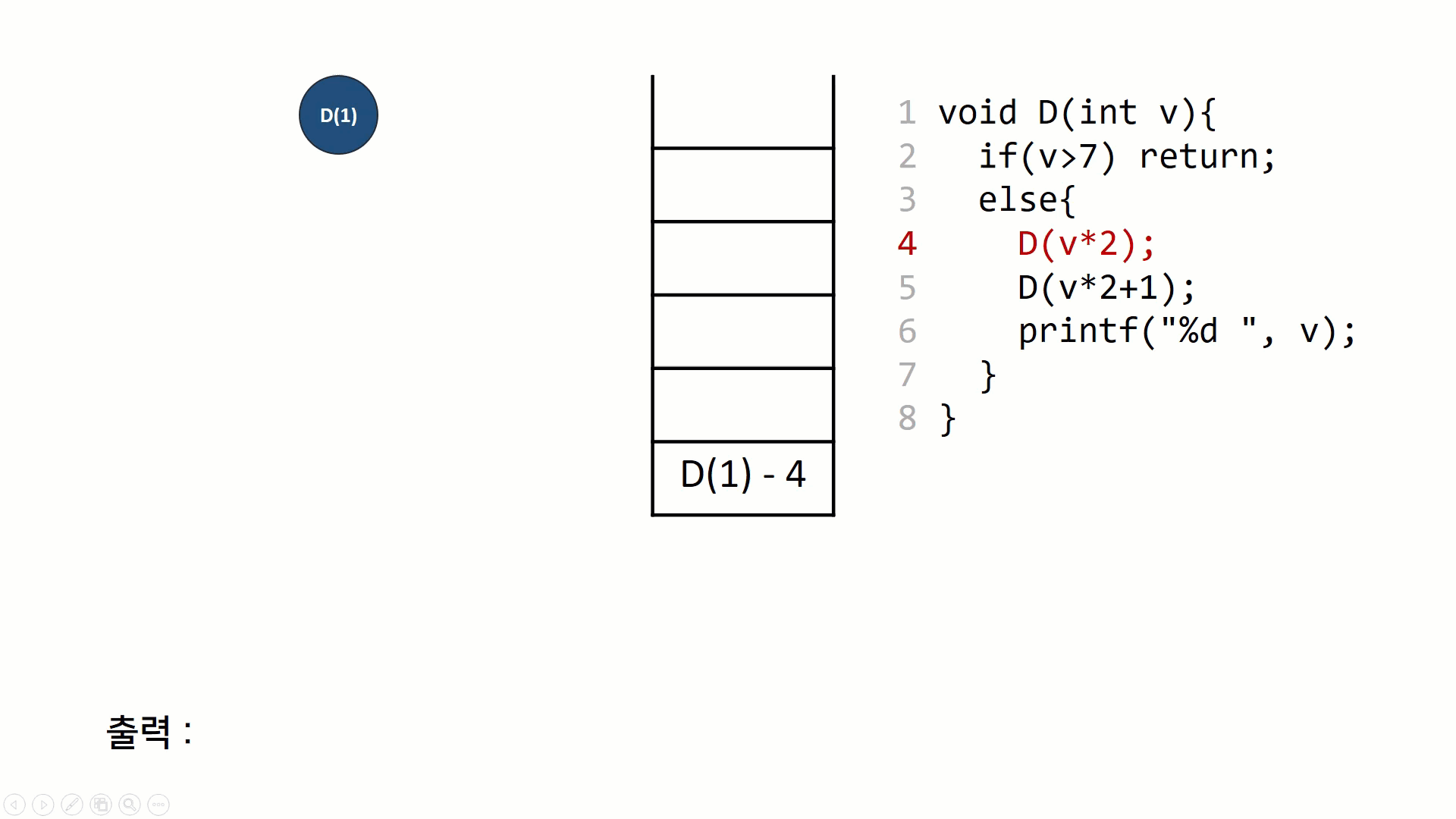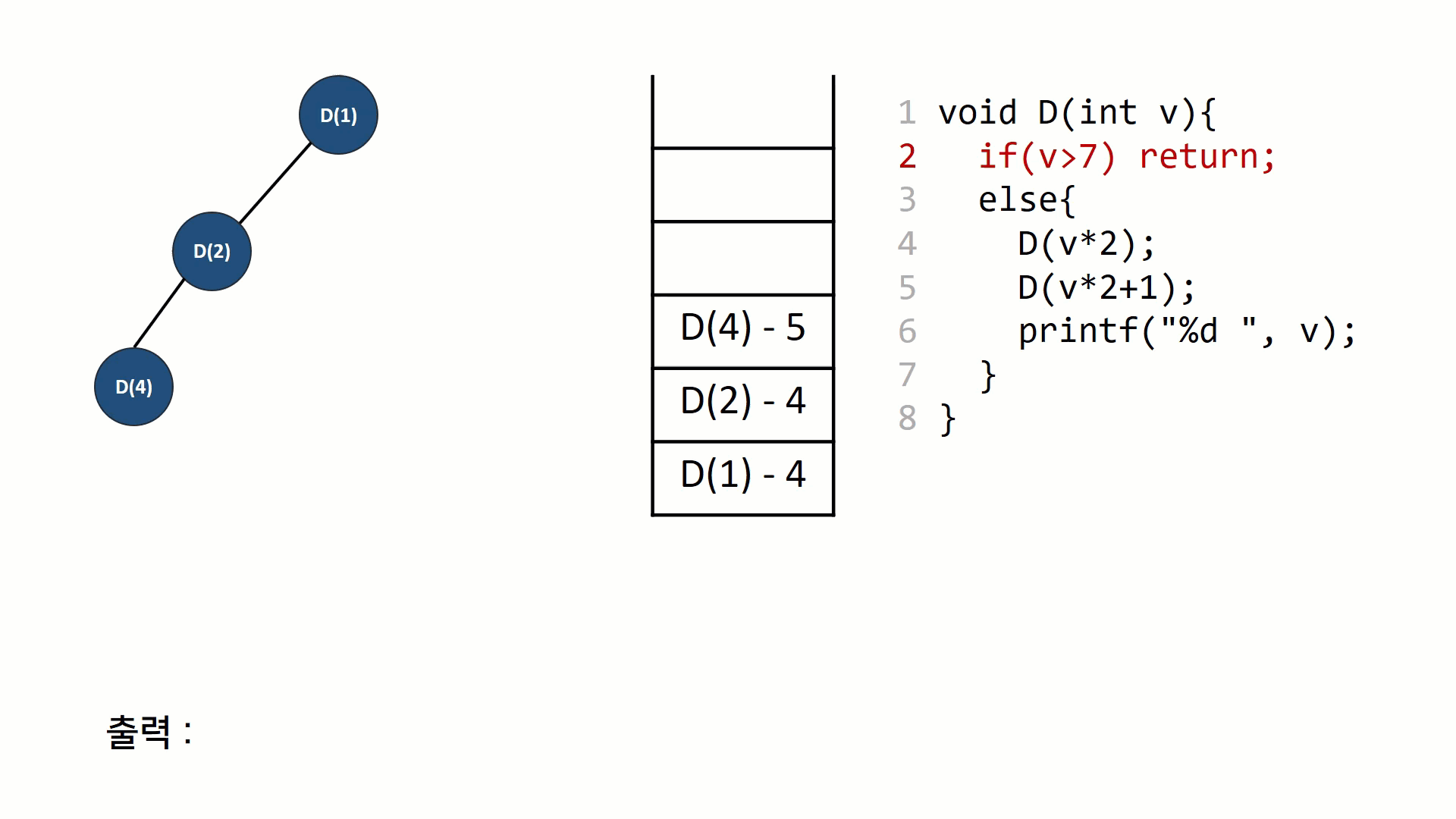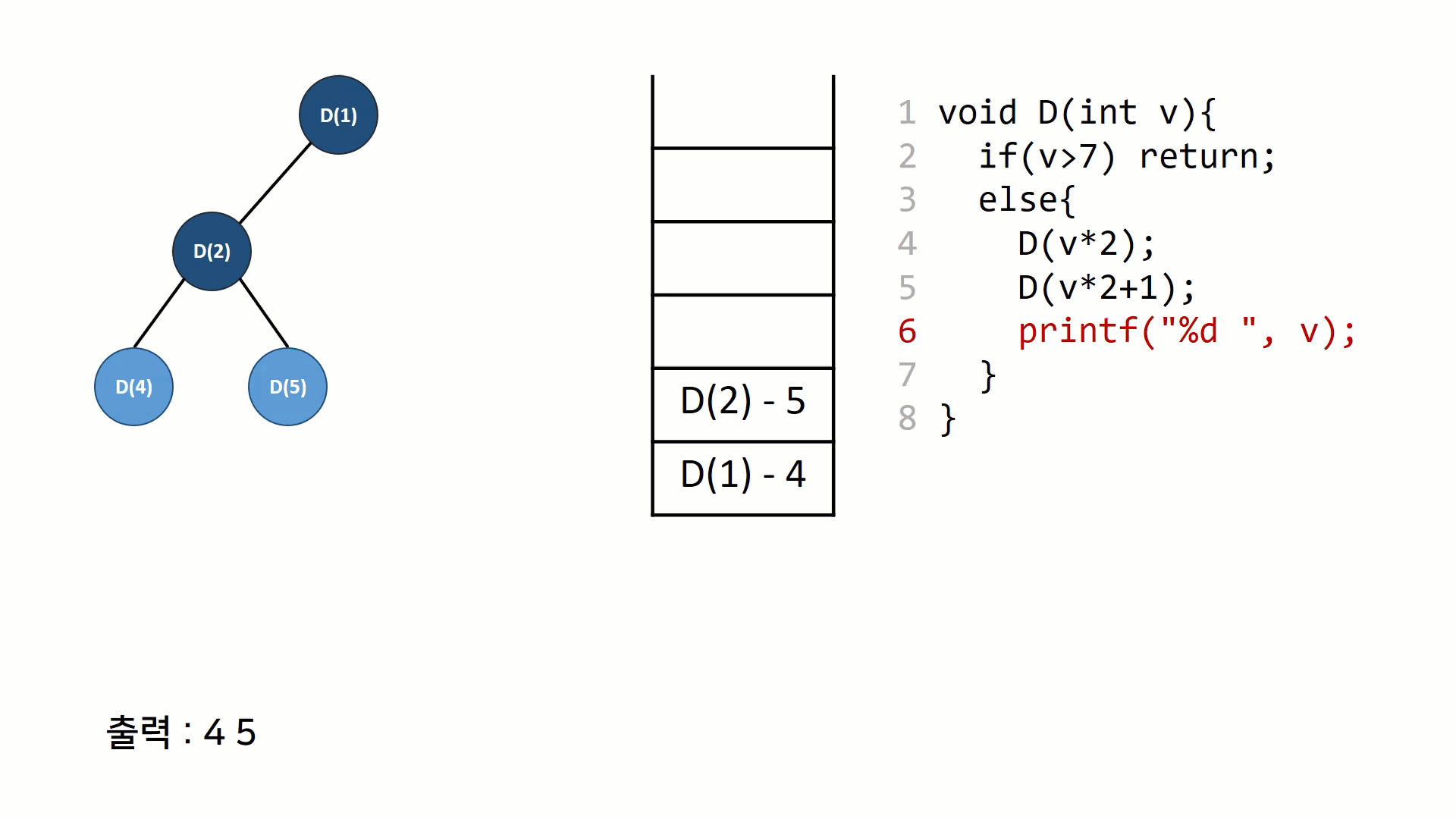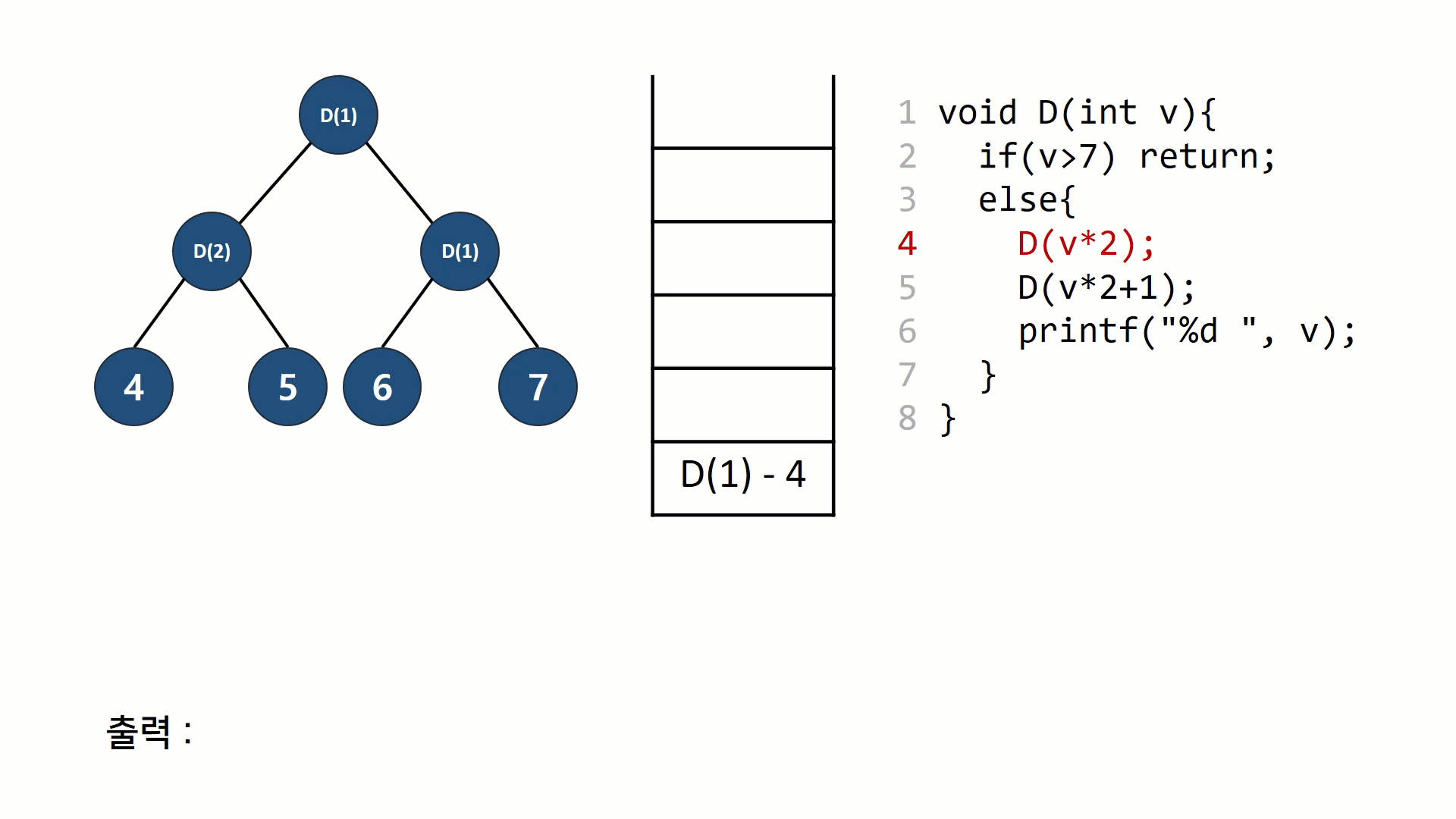
후위 순회의 동작을 나타낸 그림이다. 재귀의 호출 구조(스택 구조)를 트리의 형태로 나타내고, 똑같은 과정을 스택구조로 나타내 보았다. 일반적인 함수의 호출 규약과 동일한데, 리턴주소를 저장하고 다음 함수를 push하고 다 끝나면 pop하는 것을 반복한다.