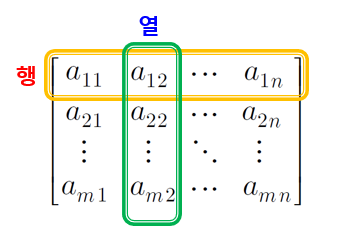
행렬(Matrix)

수나 식을 사각형 모양으로 배열하고 괄호로 묶어 놓은 것

• 성분(원소, element)
• 행(row)
• 열(column)
  

행렬의 연산

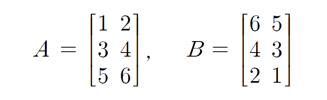
합(덧셈)

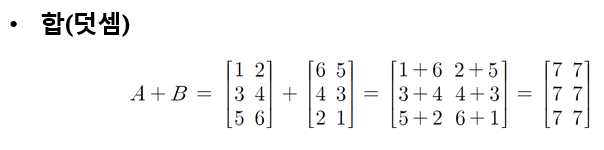
차(뺄셈)

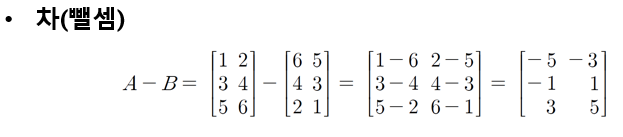
스칼라배(스칼라곱)

곱 연산

[ A의 열 개수와 B의 행 개수가 같을 때 AB의 곱 ]

---

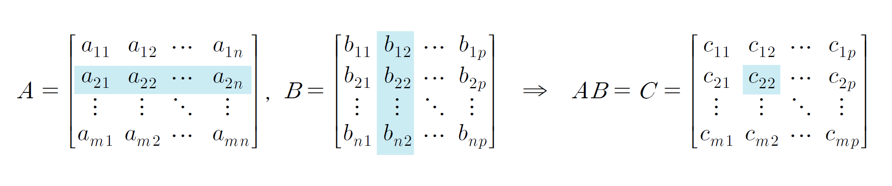
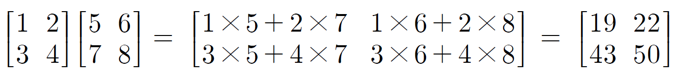
벡터(vector)

행이나 열이 하나 밖에 없는 행렬

---

선형대수학(linear algebra)

• 연립선형방정식, 벡터공간, 선형변환, 행렬을 다루는 수학 분야

선형방정식(linear equation)

• 최고차항의 차수가 1인 방정식 (=일차 방정식)

연립선형방정식(system of linear equations)

• 여러 선형방정식이 모여 있는 것
• 연립선형방정식의 해(solution)는 모든 선형 방정식을 만족하는 미지수들의 값이다

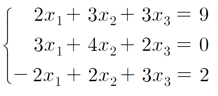
백터공간(vector space)

• 서로 더하거나 스칼라배할 수 있는 벡터들의 모음
  

선형변환(linear transformation)

행렬 이론

• 행렬의 성질과 변환에 대한 이론