선형방정식

미지수를 나타내는 변수 x1, x2, ..., xn과 상수 a1, a2, ..., an, b에 대하여, a1x1 + a2x2 + ... + anxn = b 와 같은 방정식을 선형방정식이라 한다. 선형 방정식은 일차방적식이라고도 한다

연립선형방정식

특정 미지수에 대한 선형방정식들이 모여 있는 것을 연립선형방정식 또는 선형시스템이라고 한다

불능과 부정

연린선형방정식의 해가 존재하지 않으면, 이 연립선형방정식은 불능 또는 모순이라 한다.

연립선형방정식의 해가 무수히 많으면, 이 연립선형방정식은 부정이라 한다.

동치

같은 미지수에 대하여, 두 연립선형방정식이 동일한 해집합을 가지면, 두 연립선형방정식은 동치라고 한다.

---

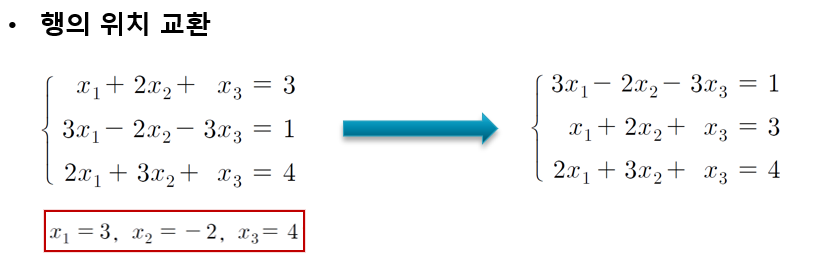
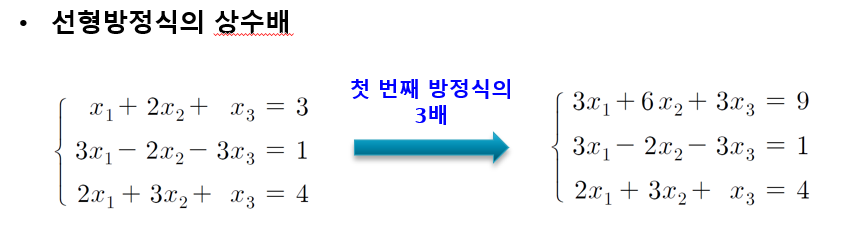
연립선형방정식의 풀이법

대입법

특정 미지수를 다른 미지수(들)의 식으로 표현하여, 해당 미지수에 이 식을 대입해서 해를 구하는 방법

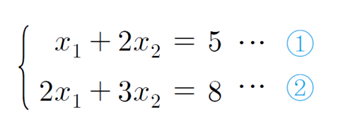
소거법

동치인 연립선형방정식을 만드는 연산을 사용해 방정식에서 미지수를 제거하며 해를 구하는 방법

---

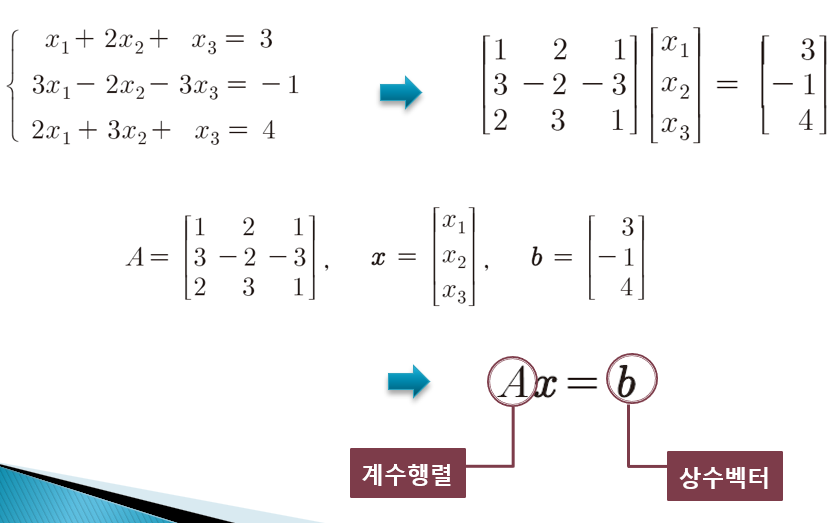
연립선형방정식의 행렬 표현

연립선형방정식을 행렬과 벡터의 곱을 Ax=b 와 같이 표현한 것을 행렬방정식이라고 함

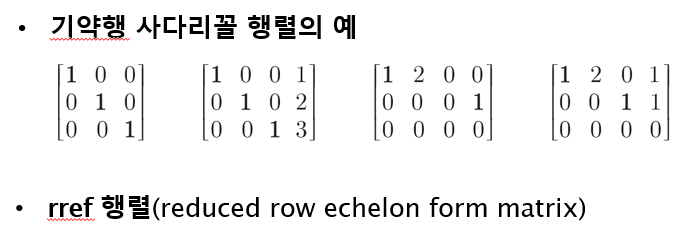
행 사다리꼴 행렬과 기약행 사다리꼴 행렬

• 추축성분(피벗)

  행렬에서 각 행의 왼쪽에 있는 0이 아닌 성분을 추축성분(pivot entry) 또는 피벗(pivot)이라 한다.

---

가우스-조단 소거법(Gauss-Jordan elimination method)

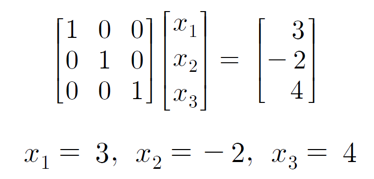
• 연립선형방정식을 표현한 행렬방정식을 계수행렬 부분을 기약행 사다리꼴 행렬로 변환하여 해를 구하는 방법
• 행렬방정식 Ax=b 에 행 연산을 하여 좌변의 행렬 A를 I로 만들면, 행렬방정식의 해를 구할 수 있음

불능인 연립선형방정식의 풀이법

• 자유변수(free variable) 도입

---

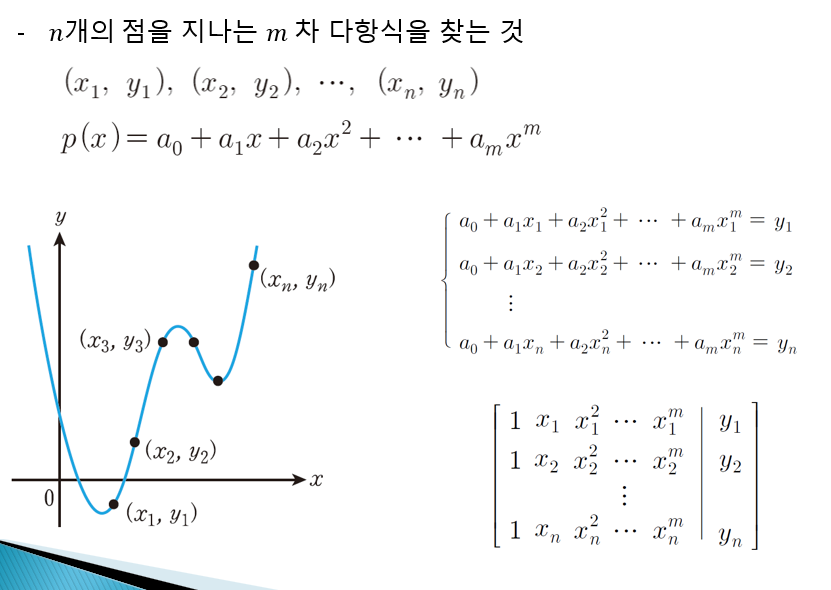
다항식 곡선 맞춤