자료구조(?) - 탐색

Pongchi·2022년 6월 10일

대학교 수업 정리 알고리즘 자료구조

마지막 수업 시간에 할게없다고 하신 교수님은 자료구조가 아닌 알고리즘을 수업 하신 것 같다.그 과정에서 자료구조 심화내용??

탐색(search)

여러 개의 자료 중에서 원하는 자료를 찾는 작업

탐색키(search key) : 항목과 항목을 구별해주는 키(key)
탐색을 위하여 사용되는 자료구조 : 배열, 연결 리스트, 트리, 그래프 등

순차탐색(sequential search)

정렬되지 않은 배열을 처음부터 마지막까지 하나씩 검사하는 방법

시간 복잡도 : O(n)

이진탐색(binary search)

배열의 중앙에 잇는 값을 조사하여 찾고자 하는 항목이 왼쪽 또는 오른쪽 부분 배열에 있는지를 알아내어 탐색의 범위를 반으로 줄여가며 탐색 진행

조건 : 정렬된 배열

Recursion Code

int search_binary(int key, int low, int high) {
	int middle;
    if ( low <= high ) {
    	middle = (low+high) / 2;
        if ( key == list[middle] )
        	return middle;
        else if (key < list[middle])
        	return search_binary(key, low, middle-1);
        else
        	return search_binary(key, middle+1, high);
    }
    return -1;
}

Iterator Code

int search_binary(int key, int low, int high) {
	int middle;
    
    while (low <= high) {
    	middle = (low+high) / 2;
        if (key == list[middle])
        	return middle;
        else if (key > list[middle]
        	low = middle+1;
        else
        	high = middle-1;
    }
    return -1;
}

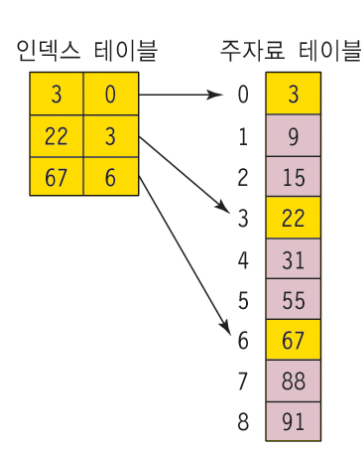
색인 순차탐색(indexed sequential search)

인덱스 테이블을 사용하여 탐색의 효율 증대
주 자료 리스트에서 일정 간격으로 발췌한 자료 저장

주 자료 리스트와 인덱스 테이블은 모두 정렬되어 있어야함
복잡도 : O(m+n/m). { 인덱스 테이블의 크기 = m, 주자료 리스트의 크기 = n)

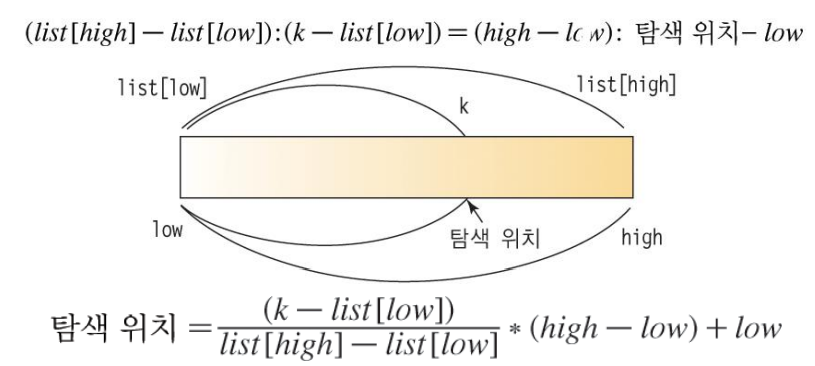
보간탐색(interpolation search)

탐색키가 존재할 위치를 예측하여 탐색하는 방법: O(log(n))

보간 탐색은 이진 탐색과 유사하나 리스트를 불균등 분할하여 탐색
보간 탐색은 데이터가 균등하게 분포되어 있을 때 유리

균형 이진탐색트리

이진 탐색과 이진 탐색 트리와 차이점

근본적으로 같은 원리에 탐색
이진 탐색은 자료들이 배열에 저장되어 있으므로 삽입/삭제 가 매우 비효율
이진 탐색 트리는 매우 빠르게 삽입/삭제 수행
삽입, 삭제가 빈번히 이뤄진다면 이진탐색트리가 유리

이진탐색트리에서의 시간복잡도

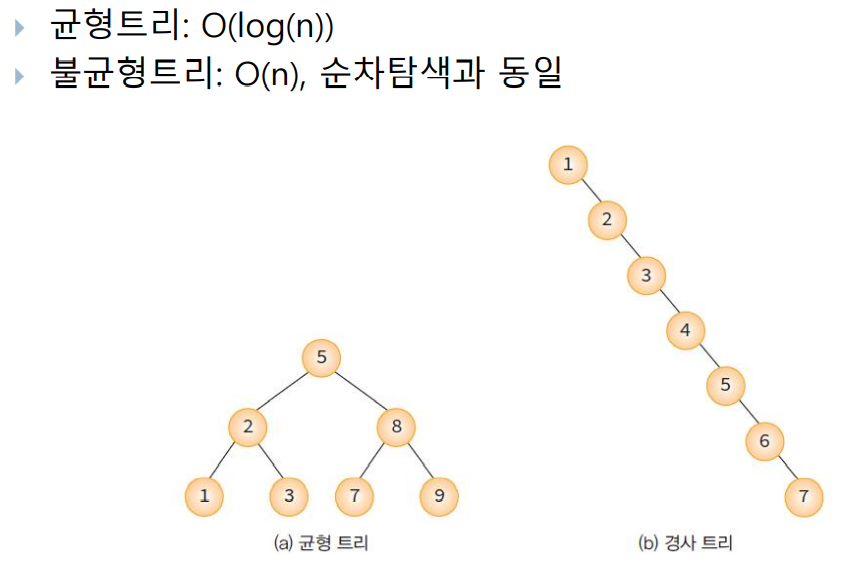
AVL 트리

모든 노드의 왼쪽과 오른쪽 서브트리의 높이 차가 1이하인 이진탐색트리

트리가 비균형 상태로 되면 스스로 노드들을 재배치하여 균형 상태 유지
평균, 최선, 최악 시간적 복잡도: O(log(n))

균형 인수(balance factor)

왼쪽 서브 트리의 높이 - 오른쪽 서브 트리의 높이

모든 노드의 균형 인수가 ±1 이하이면 AVL 트리

Code

typedef struct AVLNode {
	int key;
    struct AVLNode *left;
    struct AVLNode *right;
} AVLNode;

int get_height(AVLNode *node) {
	// 트리 강의자료 내 있다고 하시네요
}

int get_balance(AVLNode *node) {
	if (node == NULL)
    	return 0;
    return get_height(node->left) - get_height(node->right);
}

AVL 트리의 연산

탐색연산 : 이진탐색트리와 동일

삽인연산과 삭제 연산 시 균형 상태가 깨질 수 있음

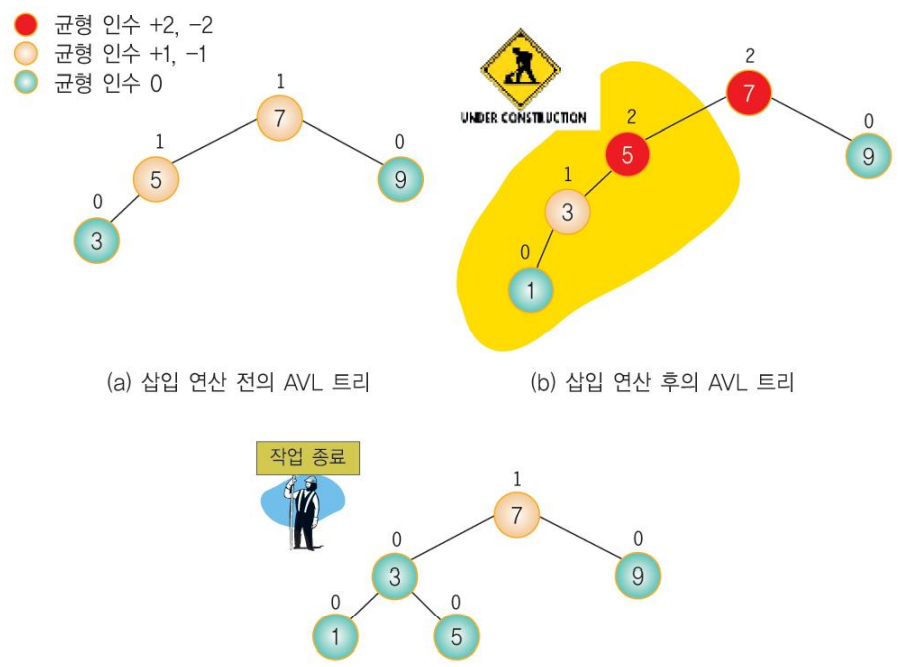
삽입연산

삽입 위치에서 루트까지의 경로에 있는 조상 노드들의 균형 인수 영향
삽입 후에 불균형 상태로 변한 가장 가까운 조상 노드(균형 인수가 ±2가 된 가장 가까운 조상 노드)의 서브 트리들에 대하여 다시 재균형
삽입 노드부터 균형 인수가 ±2가 된 가장 까가운 조상 노드까지 회전

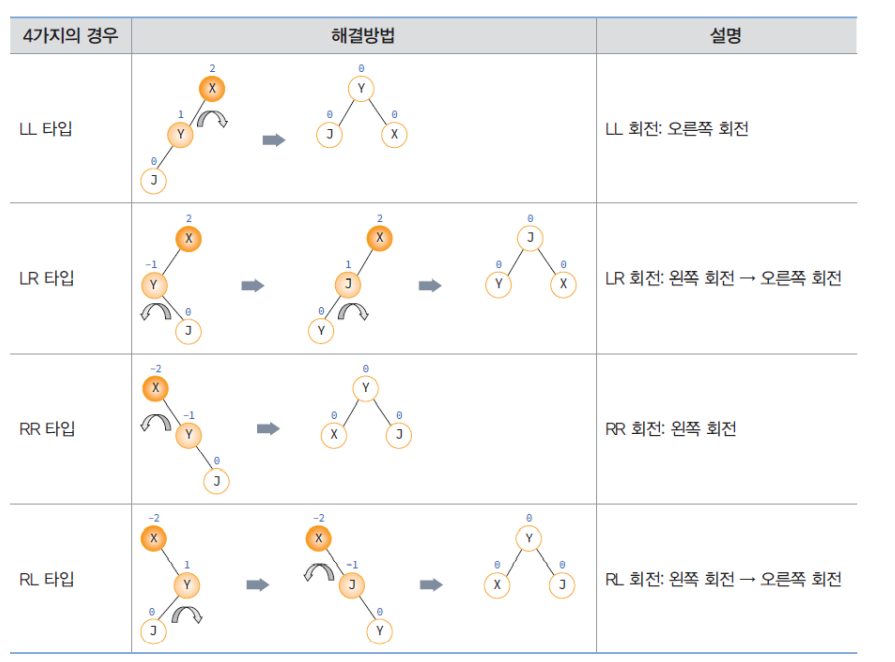
Code

AVLNode *rotate_right(AVLNode *parent) {
	AVLNode *child = parent->left;
    parent-left = child->right;
    child->right = parent;
    return child;
}

AVLNode *rotate_left(AVLNode *parent) {
	AVLNode *child = parent->right;
    parent->right = child->left;
    child->left = parent;
    return child;
}

AVLNode *rotate_left_right(AVLNode *parent) {
	parent->left = rotate_left(parent->left);
    return rotate_right(parent);
}

AVLNode *rotate_right_left(AVLNode *parent) {
	parent->right = rotate_right(parent->right);
    return rotate_left(parent);
}