우선순위 큐(priority queue)
우선순위를 가진 항목들을 저장하는 큐(queue)
- FIFO 순서가 아니라 우선 순위가 높은 데이터가 먼저 나가게 된다.
- 큐보다 우선순위 큐가 더 넓은 개념임.
큐도 다르게 보면 먼저 들어온 데이터가 우선순위가 높을 뿐임
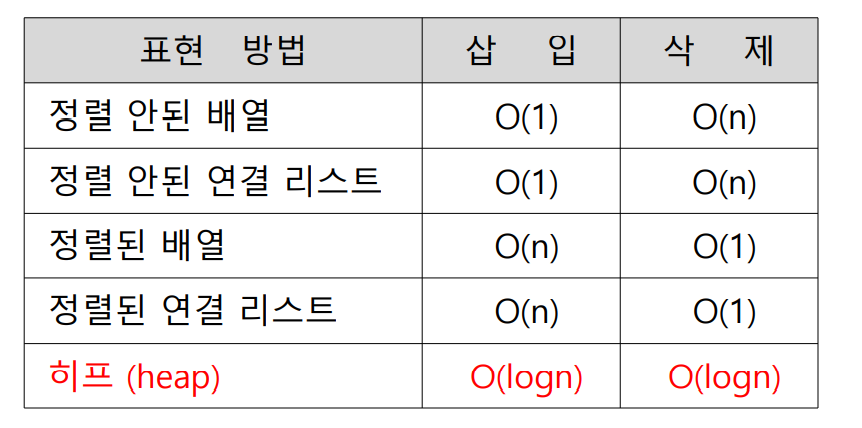
구현 방법
배열(array)을 이용한 우선순위 큐
연결리스트(linked list)를 이용한 우선순위 큐
히프(heap)를 이용한 우선순위 큐
정렬된 배열
- 우선순위를 기준으로 오름차순으로 정렬
- 가장 우선순위가 큰 데이터는 항상 배열의 마지막에 위치
- 삽입함수는 삽입 위치를 찾아야함
* 키 값을 기준으로 처음부터 삽입 위치까지 탐색. O(n)- 해당 위치에 키 입력을 위한 데이터 이동 필요 O(n)
- 따라서 삽입 시, 시간 복잡도는 O(n). ( 좀 더 정확하겐 2n 이겠죠? )
- 삭제함수는 마지막 데이터를 리턴, 배열 데이터의 개수를 하나 줄임
* 삭제 시, 시간 복잡도는 O(1)
정렬 안된 배열
- 삽입 함수는 새로운 데이터를 무조건 배열 끝에 붙임
* 시간 복잡도 O(1) - 삭제 함수는 삭제할 데이터를 찾아야함
* 삭제 시, 가장 높은 우선 순위를 처음부터 끝까지 뒤져야야함
so, 시간복잡도 O(n)- 삭제 후, 데이터 이동 필요. 시간 복잡도 O(n)
- 따라서, 삭제의 시간 복잡도 O(n)
- 삭제 후, 데이터 이동 필요. 시간 복잡도 O(n)
정렬된 연결 리스트
- 우선순위를 기준으로 내림차순으로 정렬
- 우선순위가 가장 높은 데이터를 헤드 포인터가 직접 가르킴
- 삭제의 시간복잡도 O(1)
- 삽입함수는 O(n)
정렬 안된 연결 리스트
- 삽입될 데이터를 가장 첫 노드에 삽입.
- 시간복잡도 O(1)
- 삭제는 탐색을 해야하기에 O(n)
히프(Heap)
우선순위 큐를 위해 만들어진 자료구조
- 히프란 노드들이 저장하고 있는 키들이 다음과 같은 식을 만족하는 완전이진트리(complete binary tree)
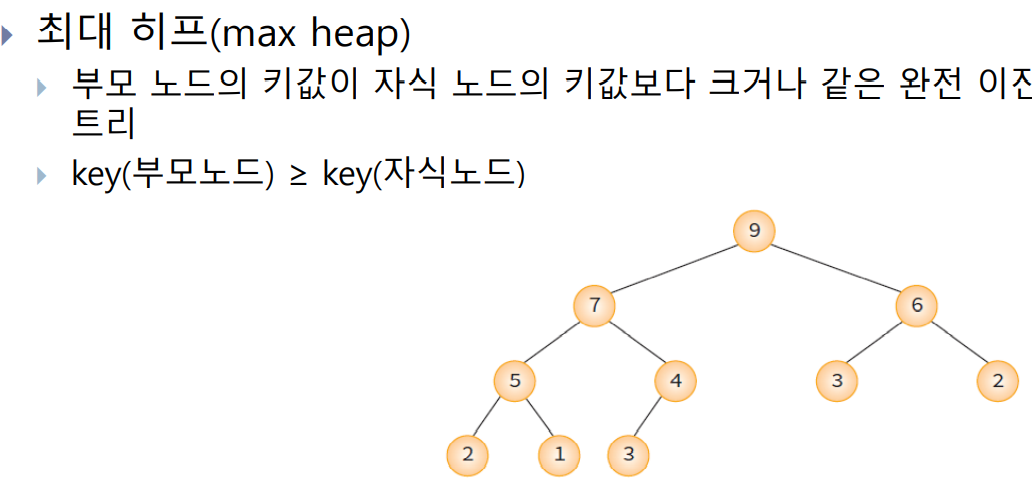
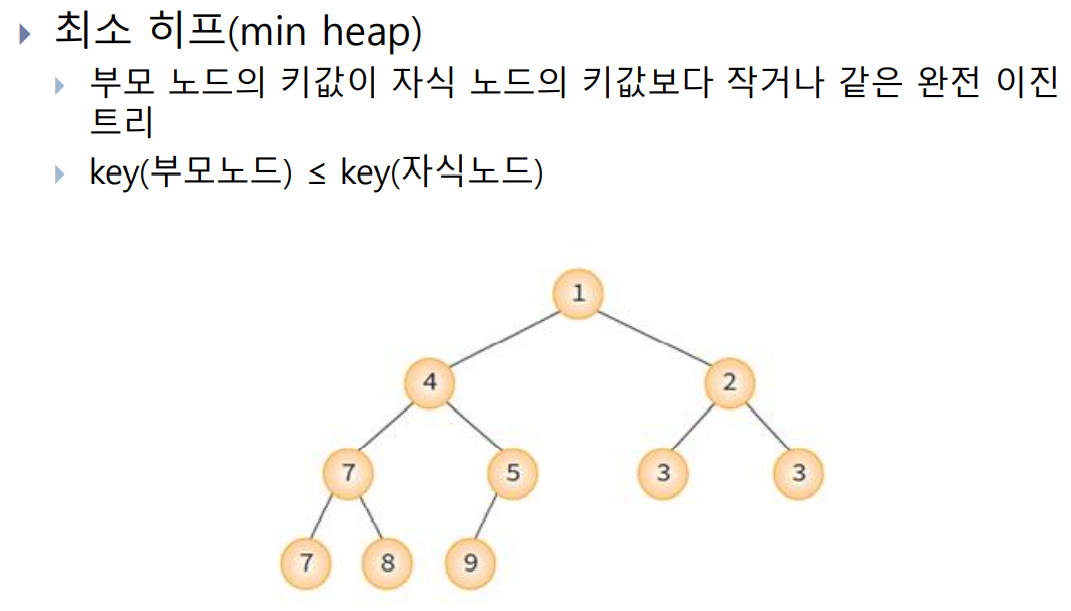
- 히프는 최대 히프(max heap)와 최소 히프(min heap)가 있음.
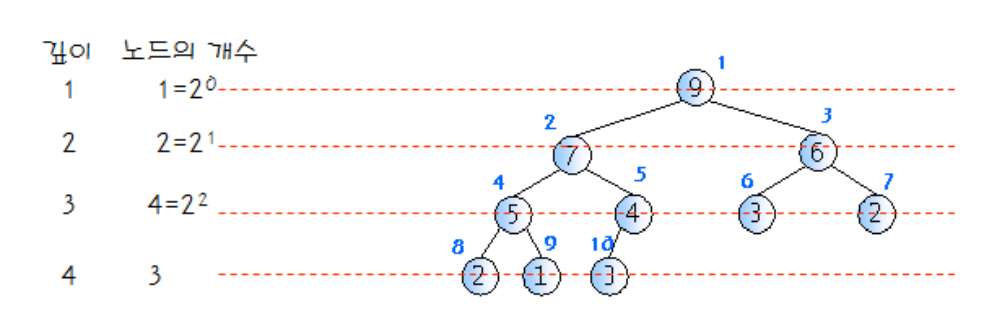
히프의 높이
n개의 노드를 가지고 있는 히프의 높이는 logn
히프의 구현 방법
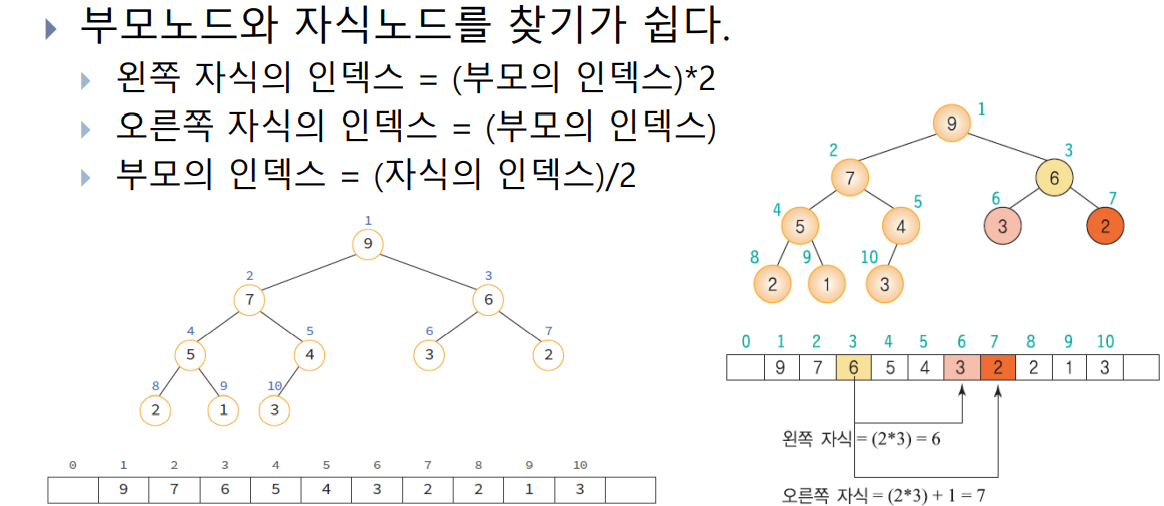
히프는 배열을 이용하여 구현
- 완전이진트리이므로 각 노드에 번호를 붙일 수 있음
- 이 번호를 배열의 인덱스라고 생각
히프에서 삽입
- 새로운 요소가 들어오면, 일단 새로운 노드를 히프의 마지막 노드에 이어서 삽입
- 삽입 후에 새로운 노드를 부모 노드들과 비교 및 교환해서 히프의 성질을 만족
- 키 k가 부모 노드보다 작거나 같으면 삽입 연산은 종료 ( 최대 히프의 경우 )
- 히프의 높이가 O(logn)이므로 히프의 삽입연산은 O(logn)
히프에서 삭제
- 최대 히프에서의 삭제는 가장 큰 키 값을 가진 노드를 삭제하는 것을 의미. 즉, 루트 노드가 삭제됨
- 루트 노드를 삭제한다.
- 마지막 노드를 루트 노드로 이동한다.
- 루트에서부터 단말 노드까지의 경로에 있는 노드들을 교환하여 히프 성질을 만족
- 히프의 높이가 O(logn)이므로 히프의 삭제연산은 O(logn)
구현 코드
#define MAX_ELEMENT 200
typedef struct {
int key;
} element;
typedef struct {
element heap[MAX_ELEMENT];
int heap_size;
} HeapType
void insert_max_heap(HeapType *h, element item) {
int i;
i = ++(h->heap_size);
while ( (i != 1) && (item.key > h->heap[i/2].key) ) {
h->heap[i] = h->heap[i/2];
i /= 2;
}
h->heap[i] = item;
}
element delete_max_heap(HeapType *h) {
int parent, child;
element item, temp;
item = h->heap[1];
temp = h->heap[(h->heap_size)--];
parent = 1;
child = 2;
while (child <= h->heap_size) {
if ( (child < h->heap_size) && (h->heap[child].key) < h->heap[child+1].key)
child++;
if (temp.key >= h->heap[child].key)
break;
h->heap[parent] = h->heap[child];
parent = child;
child *= 2;
}
h->heap[parent] = temp;
return item;
}히프 정렬
- 먼저 정렬해야 할 n개의 요소들을 최대 히프에 삽입
- 히프에서 삭제 시 키가 가장 큰 레코드가 빠져 나옴
- 빈 트리가 될 때까지 계속적으로 삭제를 가함
- 빠져 나온 레코드를 순차적으로 적어나가면 그것이 바로 정렬된 결과
- 히프 정렬이 최대로 유용한 경우는 전체 자료를 정렬하는 것이 아니라 가장 큰 값 몇 개만 필요할 떄임
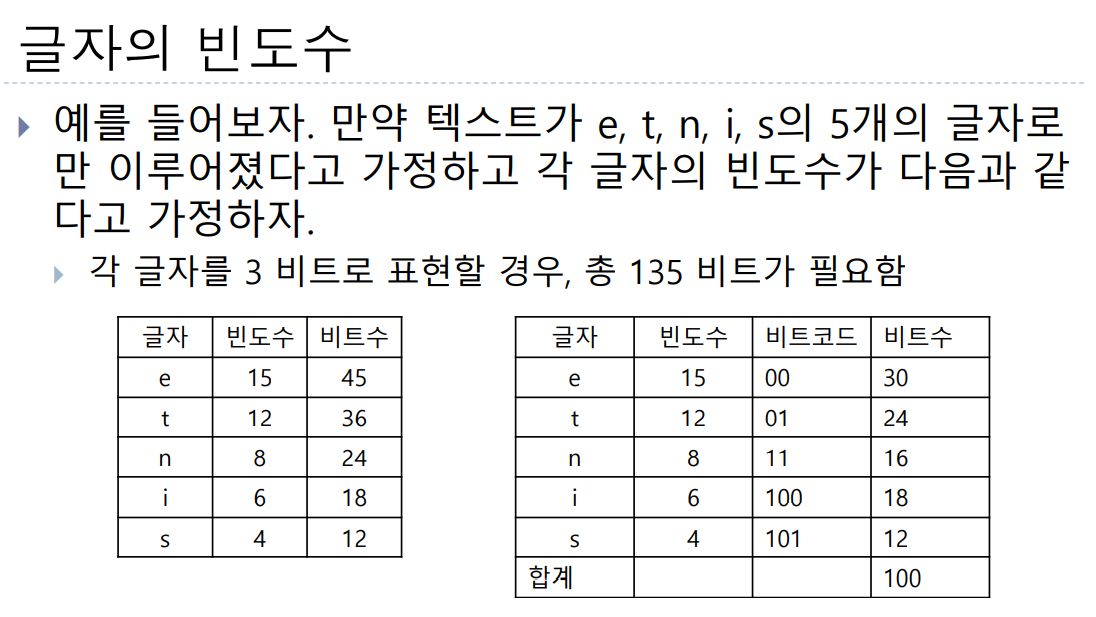
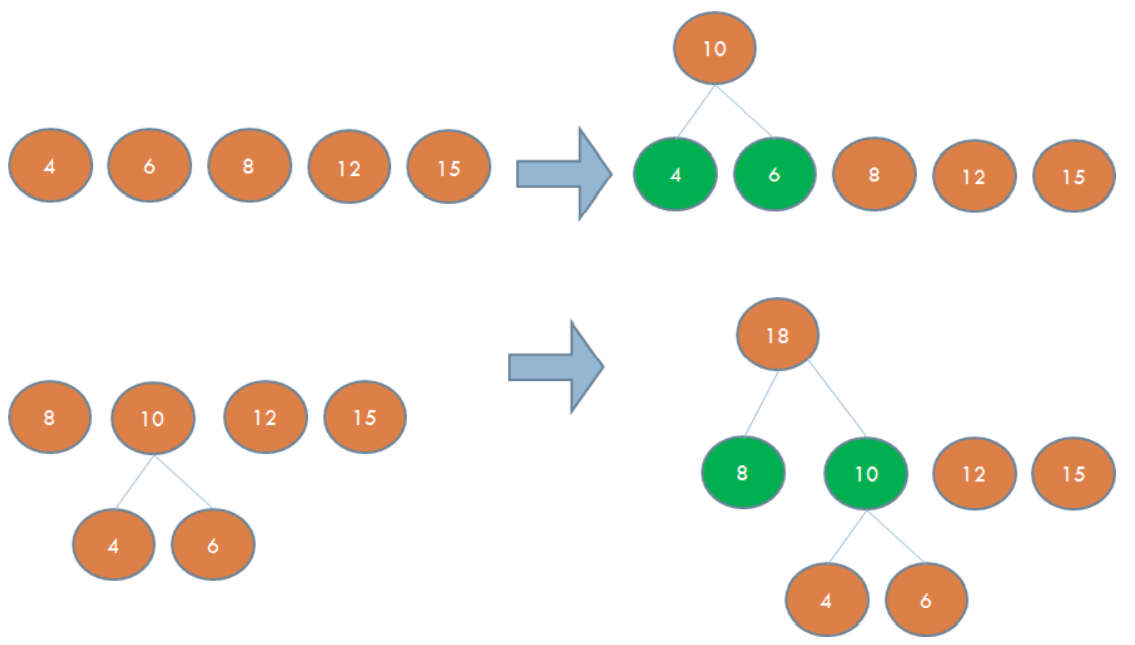
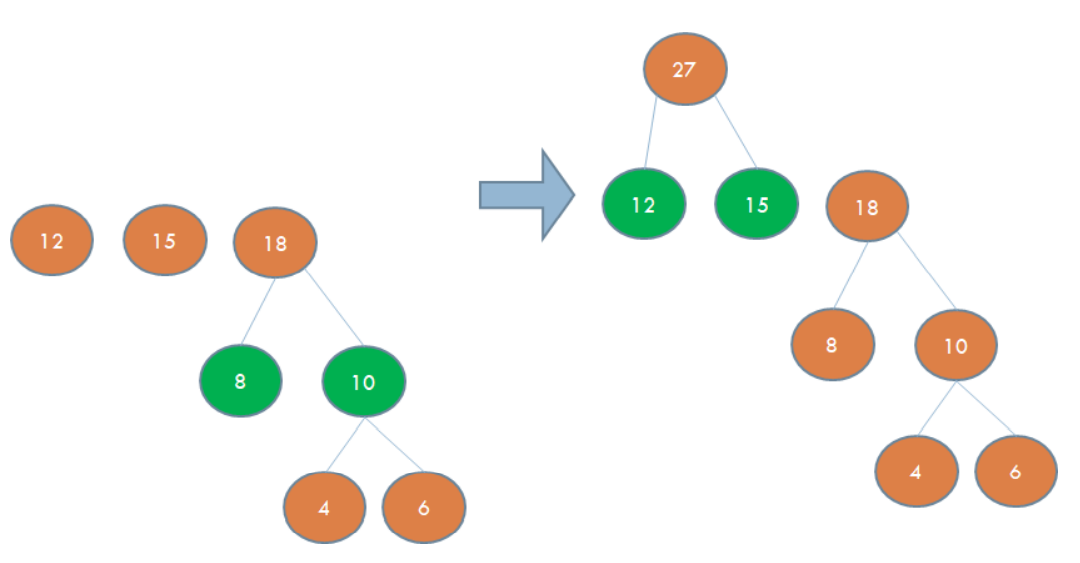
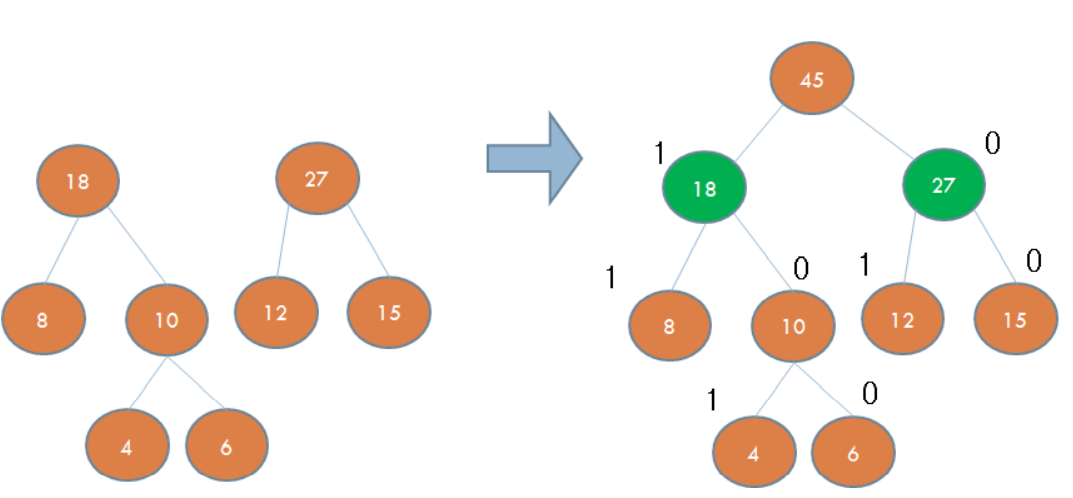
허프만 코드
- 이진 트리는 각 글자의 빈도가 알려져 있는 메시지의 내용을 압축하는데 사용할 수 있음
- 이런 종류의 이진트리를 허프만 코딩 트리라고 부름