트리(Tree)

계층적인 구조를 나타내는 자료구조
( 리스트, 스택, 큐 등은 선형 구조 )

트리는 부모-자식 관계의 노드들로 이루어진다

응용 분야:

• 계층적인 조직 표현
• 컴퓨터 디스크의 디렉토리 구조
• 인공지능에서의 결정트리 (decision tree)

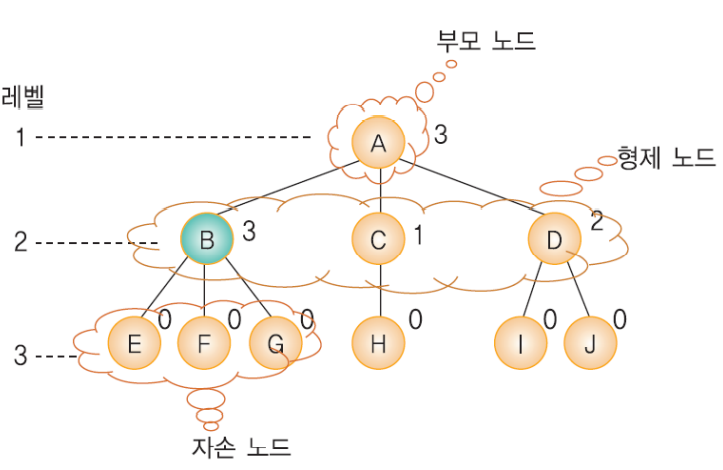
트리의 용어

노드(node)

트리의 구성요소

루트(root)

부모가 없는 노드

서브트리(subtree)

하나의 노드와 그 노드들의 자손들로 이루어진 트리

단말노드(terminal node)

자식이 없는 노드

비단말노드

적어도 하나의 자식을 가진 노드

자식, 부모, 형제, 조상, 자손 노드

차수(degree)

노드가 가지고 있는 자식 노드의 개수

레벨(level)

트리의 각층의 번호

높이(height)

트리의 최대 레벨

---

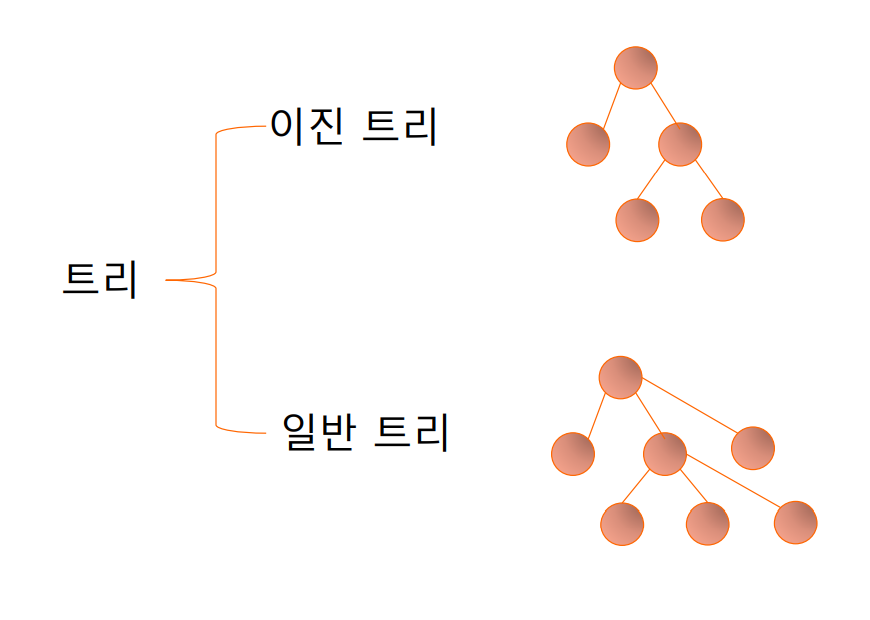
트리의 종류

크게 이진 트리와 일반 트리로 나뉨

---

이진 트리 (binary tree)

모든 노드가 최대 2개의 서브 트리를 가지고 있는 트리
서브트리는 공집합일 수 있음

이진 트리의 성질

1. 노드의 개수가 n개 이면 간선의 개수는 n-1
   

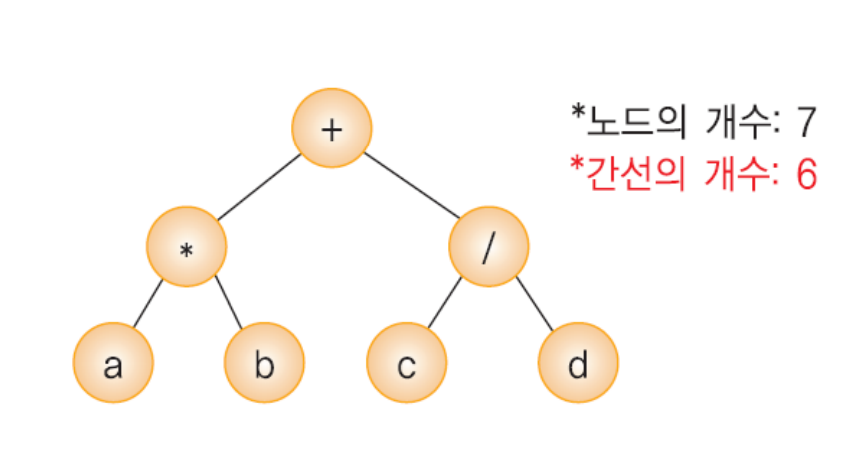
2. 높이가 h인 이진트리의 경우, 최소 h개의 노드를 가지며 최대 2^h -1개의 노드를 가짐
   

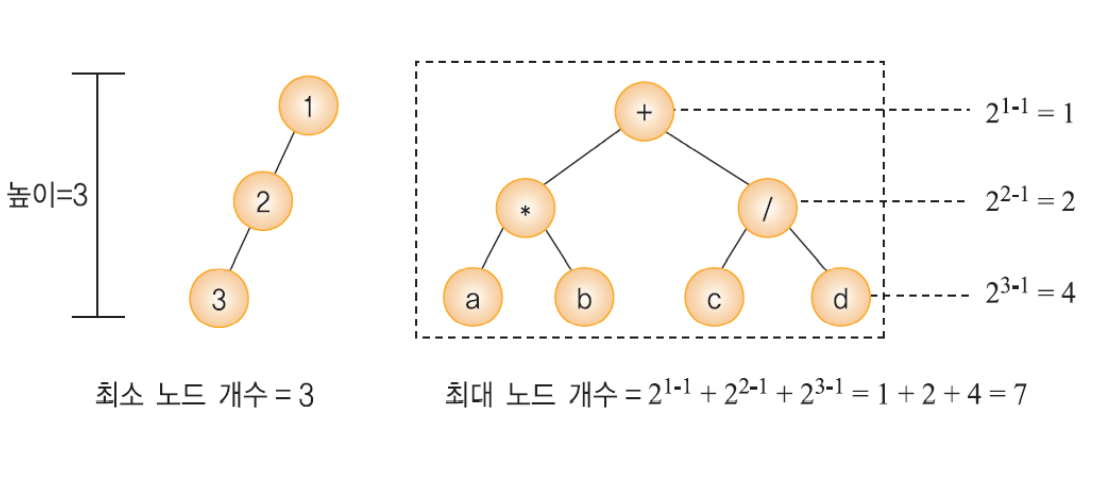
3. n개의 노드를 가지는 이진트리의 높이
   

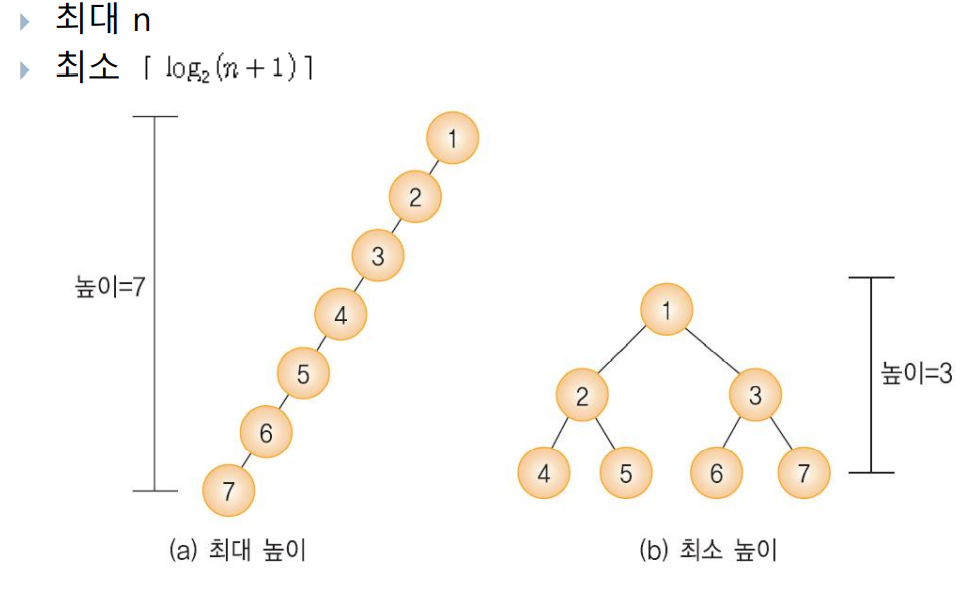
이진 트리의 분류

1. 포화 이진 트리(full binary tree)
2. 완전 이진 트리(complete binary tree)
3. 기타 이진 트리
   

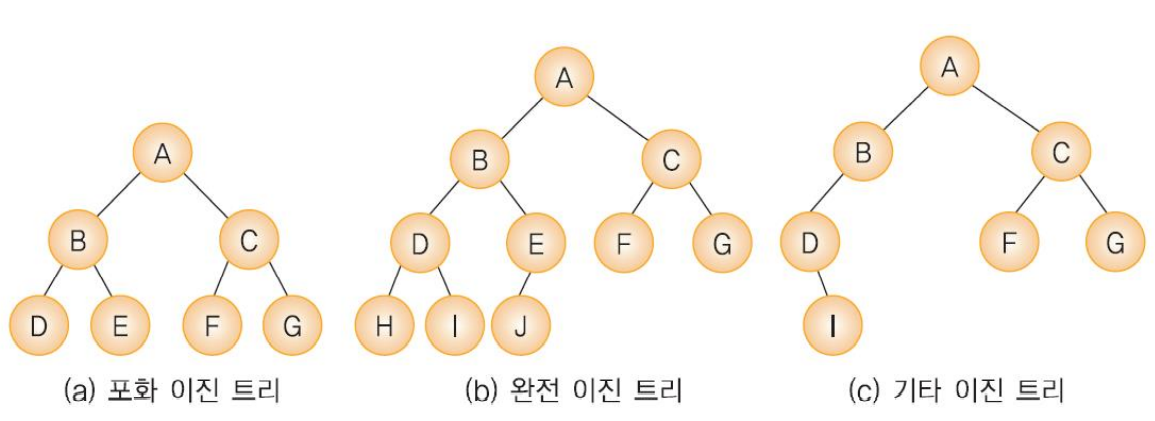
포화 이진 트리(full binary tree)

용어 그대로 트리의 각 레벨에 노드가 꽉 차있는 이진트리를 의미함

완전 이진 트리(complete binary tree)

레벨 1부터 k-1까지는 노드가 모두 채워져 있고 마지막 레벨 k에서는 왼쪽부터 오른쪽으로 노드가 순서대로 채워져 있는 이진트리

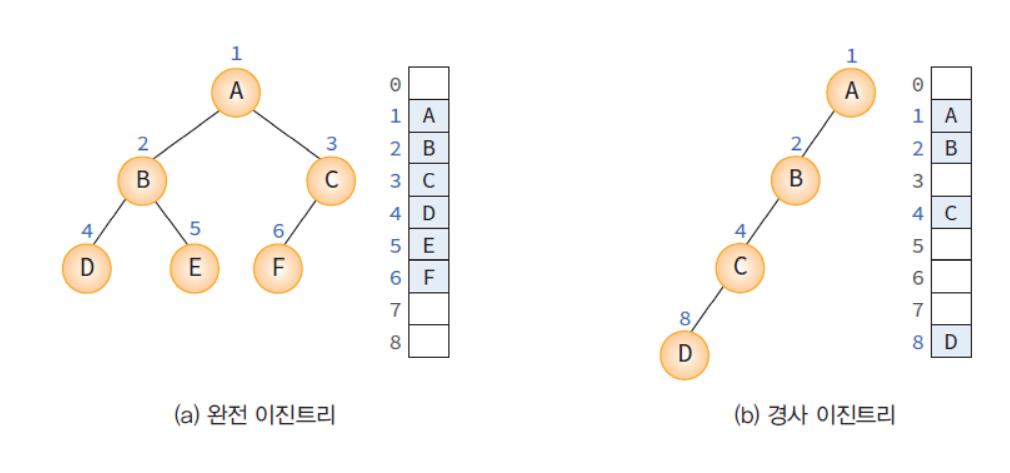
이진 트리의 표현 - 배열

모든 이진 트리의 포화 이진 트리라고 가정하고 각 노드에 번호를 붙여서 그 번호를 인덱스로 삼아 노드의 데이터를 배열에 저장하는 방법

부모와 자식 인덱스 관계

• 노드 i의 부모 노드 인덱스 = i/2
• 노드 i의 왼쪽 자식 노드 인덱스 = 2i
• 노드 i의 오른쪽 자식 노드 인덱스 = 2i + 1

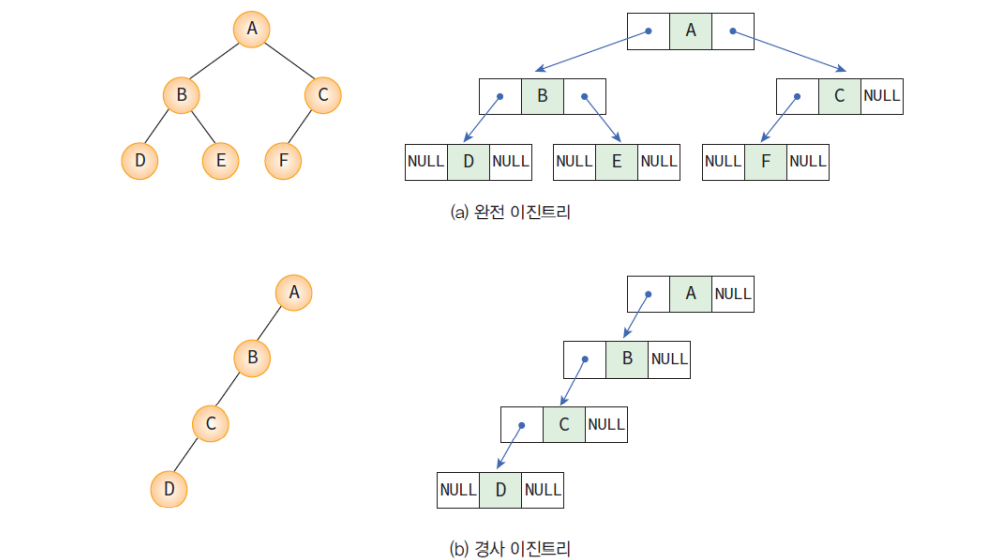
이진 트리의 표현 - 링크

포인터를 이용하여 부모노드가 자식노드를 가르키게 하는 방법

구현 코드.

노드는 구조체로, 링크는 포인터로 표현

typedef struct TreeNode {
	int data;
    struct TreeNode *left, *right;
} TreeNode;

void main()
{
	TreeNode *n1, *n2, *n3;
    
    n1 = (TreeNode *)malloc(sizeof(TreeNode));
    n2 = (TreeNode *)malloc(sizeof(TreeNode));
    n3 = (TreeNode *)malloc(sizeof(TreeNode));
    
    n1->data = 10;
    n1->left = n2;
    n2->right = n3;
    
    n2->data = 20;
    n2->left = NULL;
    n2->right = NULL;
    
    n3->data = 30;
    n3->left = NULL;
    n3->right =NULL;
}

---

이진 트리의 순회

순회

트리의 노드들을 체계적으로 방문하는 것

3가지의 기본적인 순회방법

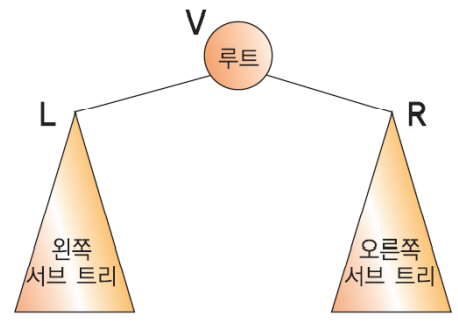
• 전위순회(preorder traversal) : VLR, 자손노드보다 루트노드를 먼저 방문
• 중위순회(inorder traversal) : LVR, 왼쪽 자손, 루트, 오른쪽 자손 순으로 방문
• 후위순회(postorder traversal) : LRV, 루트노드보다 자손을 먼저 방문
  

전위 순회

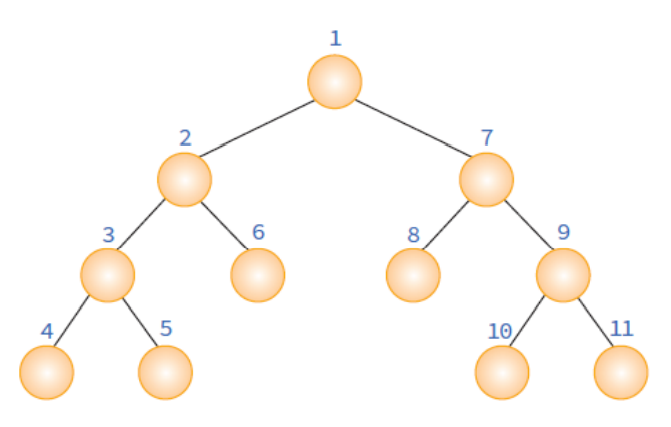
// 의사코드(Pseudo-code)
preorder(x)
	if x!=NULL
    	print DATA;
        preorder(LEFT(x));
        preorder(RIGHT(x));

중위 순회

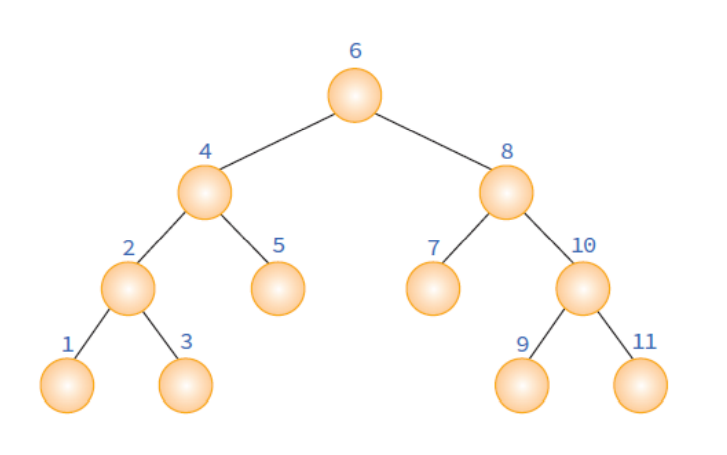
inorder(x)
	if x!= NULL
    	inorder(LEFT(x));
        print DATA(X);
        inorder(RIGHT(x));

후위 순회

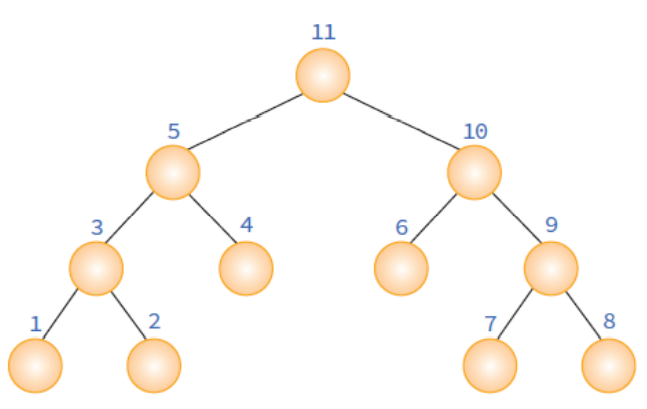
postorder(x)
	if x!= NULL
    	postorder(LEFT(x));
        postorder(RIGHT(x));
        print DATA(x);

---

레벨 순회

각 노드를 레벨 순으로 검사하는 순회 방법

• 지금까지 순회 법이 스택을 사용했던 것에 비해 레벨 순회는 큐는 사용하는 순회 법

// pseudo-code
level_order(root)
{
	initialize queue;
    enqueue(queue, root);
    while is_empty(queue) != TRUE do
    	x <- dequeue(queue);
        if (x != NULL)
        	print( DATA(x);
        enqueue(queue, LEFT(x));
        enqueue(queue, RIGHT(x));
}