자료구조 - 트리 (2)

Pongchi·2022년 6월 9일

이진탐색트리

탐색작업을 효율적으로 하기 위한 자료구조

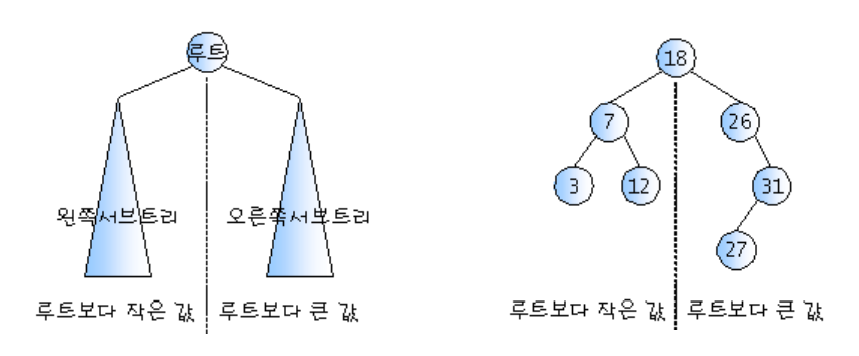
왼쪽서브트리 <= 루트노드 <= 오른쪽서브트리
이진탐색을 중위순회하면 오름차순으로 정렬된 값을 얻을 수 있음

탐색

비교한 결과가 같으면 탐색이 성공적으로 끝남

주어진 키 값이 루트 노드의 키 값보다 작으면 왼쪽 자식을 기준으로 다시 시작

주어진 키 값이 루트 노드의 키 값보다 크면 오른쪽 자식을 기준으로 다시 시작

순환적인 방법

TreeNode *search(TreeNode *node, int key)
{
	if (node == NULL)
    	return NULL;
    if (key == node->key)
    	return node;
    else if (key < node->key )
    	return search(node->left, key);
    else
    	return search(node->right, key);
}

반복적인 방법

TreeNode *search(TreeNode *node, int key)
{
	while (node != NULL) {
    	if (key == node->key)
        	return node;
        else if (key < node->key)
        	return node = node->left;
        else
        	node = node->right;
    }
    return NULL;
}

이진탐색트리에서의 삽입연산

원소를 삽입하기 위해서는 먼저 탐색을 수행하는 것이 필요
탐색에 실패한 위치가 바로 새로운 노드를 삽입하는 위치

void insert_node(TreeNode **root, int key) {
	TreeNode *p, *t;
    TreeeNode *n;
    t = *root;
    p = NULL;
    
    while (t != NULL) {
    	if (key == t->key)
        	return;
        
        p = t;
        if (key < t->key )
        	t = t->left
        else
        	t = t->right
    }
    // 데이터 복사
    n = (TreeNode *)malloc(sizeof(TreeNode));
    if (n == NULL)
    	return;
    n->key = key;
    n->left = n->right = NULL;
    
    // 부모 노드와 링크 연결
    if (p != NULL)
    	if (key < p->key)
        	p->left = n;
        else
        	p->right = n;
    else
    	*root = n;
}

이진탐색트리에서의 삭제연산

3가지의 경우

삭제하려는 노드가 단말 노드 일 경우

삭제하려는 노드가 하나의 왼쪽이나 오른쪽 서브 트리 중 하나만 가지고 있는 경우

삭제하려는 노드가 두개의 서브 트리 모두 가지고 있는 경우

삭제하려는 노드가 단말 노드 일 경우

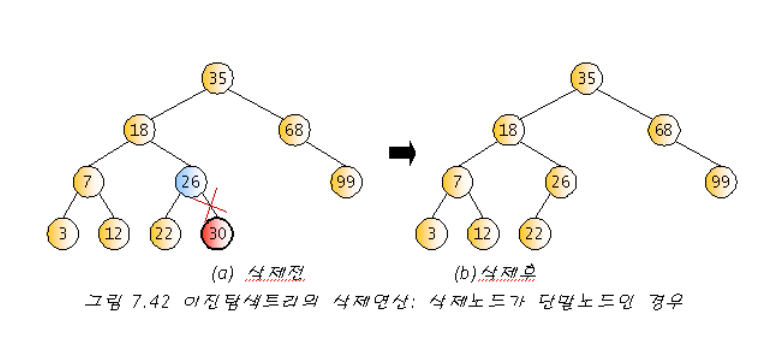
삭제하려는 노드가 하나의 서브트리만 갖고 있는 경우

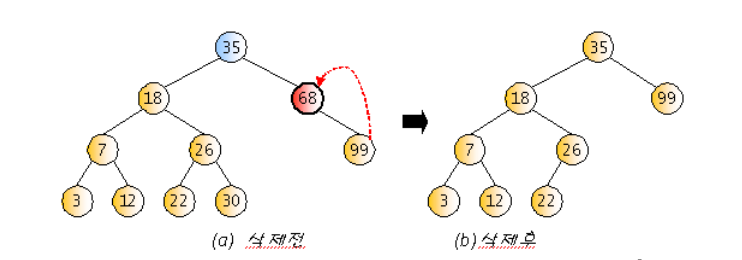
삭제하려는 노드가 두개의 서브트리를 갖고 있는 경우

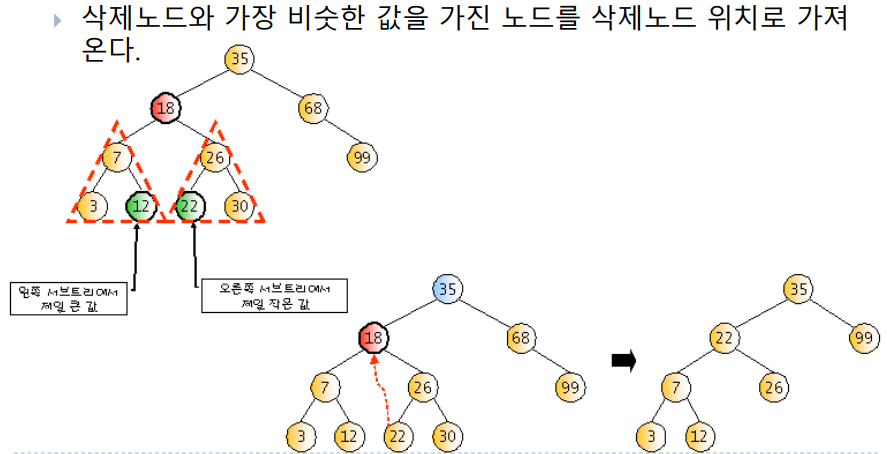
Code

void delete_node(TreeNode **root, int key) {
	TreeNode *p, *child, *succ, *succ_p, *t;
    
    // key를 갖는 노드 t를 탐색, p는 t의 부모노드
    p = NULL;
    t = *root;
    
    while ( t != NULL && t->key != key ) {
    	p = t;
        t = (key < t->key) ? t->left : t->right;
    }
    
    if (t == NULL) {
    	printf("key is not in the tree");
        return;
    }
    
    if ((t->left == NULL) && (t->right == NULL)) {
    	if (p != NULL) {
        	if (p->left = t)
            	p->left = NULL;
            else
            	p->right = NULL;
        }
    } else {
    	*root = NULL;
    }
 	else if ( (t->left == NULL) || (t->right == NULL) ) {
    	child = (t->left != NULL) ? t->left : t->right;
        if ( p != NULL) {
        	if (p->left == t)
            	p->left = child;
            else
            	p->right = child;
        } else {
        	*root = child;
        }
    }
    else {
    	succ_p = t;		succ = t->right;
        while (succ->left != NULL) {
        	succ_p = succ;		succ = succ->left
        }
        
        if (succ_p->left == succ)
        	succ_p->left = succ->right;
        else
        	succ_p->right = succ->right;
        // 후속자가 가진 키값을 현재 노드에 복사
        t->key = succ->key;
        t = succ;
    }
    free(t);
}