1. 자료구조에서 말하는 그래프란?
보통 사람들이 그래프하면 위와 같이 X축과 Y축이 있고, X와 Y의 관계를 나타내는 것을 점이나 선으로 나타낸 것을 떠오른다. 하지만 자료구조에서 그래프는 위의 그래프가 아니다.(저 그래프가 컴퓨터 공학에서 쓰이는 번지수는 따로 있다) 아래와 같이 여러개의 점들이 서로 복잡하게 연결되어 있는 관계를 표현한 자료구조를 뜻한다.
2. 그래프 용어정리
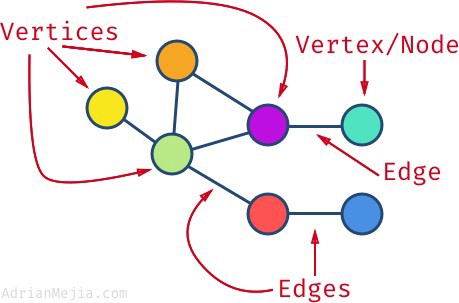
자료구조에서 그래프에서는 전문 용어가 있다. 다음은 그래프에서 자주 쓰는 용어를 정리한 것이다.
정점(Vertex): 그래프를 형성하는 노드(Node). 그래프에서 원으로 표시됨.
간선(Edge): 노드 사이를 연결한 선
(비)가중치 그래프: 간선에 대한 값이 없는 그래프
무향 그래프: 정해진 방향이 없어서 양쪽 모두 이동 가능한 그래프
진입차수(정점 차수): 해당 정점에 연결된 간선의 개수
희소 그래프: 정점 간 가능한 연결 중 일부만 존재하는 경우(일부 길이 끊어짐)
인접: 두 정점간에 간선이 직접 이어져 있는 상태
자기루프: 정점에서 진출하는 간선이 곧바로 자기 자신에게 진입하는 경우
사이클: 한 정점에서 출발하여 다시 해당 정점으로 돌아갈 수 있는 경우
3. 그래프 표시방법(1) 인접 행렬
그래프라는 것은 결국 정점간 연결 관계를 설명한 자료구조이다. 정점 사이의 연결 관계를 행렬 또는 리스트로 나타낼 수 있다. 자바스크립트에서는 행렬과 리스트라는 개념이 없기 때문에 행렬은 2차원 배열로, 리스트는 객체로 대체하여 표시한다. 여기서는 인접 행렬에 대하여 설명할 것이다.
자바스크립트에서 인접 행렬은 2차원 (n+1)X(n+1) 배열로 나타낸다. 그리고 배열의 i번째 행과 j번째 열의 인접여부에 따라서 값을 정한다. 인접하면 1을, 인접하지 않으면 0을 값으로 준다. 만약에 그래프에 가중치가 존재한다면 인접 행렬의 엘리먼트 값에 가중치를 적어준다.
인접 행렬은 표로 정리되어있기 때문에 한 정점과 다른 정점 간 인덱스만 확인해서 찾으면 바로 인접 여부를 알 수 있다. 그리고 최단거리 찾기 문제를 해결하는데 최적화되어있다.(그 알고리즘이 복잡하기는 하지만...) 다만, 정점이 자주 삭제되는 경우에는 적합하지 않다.
4. 인접 행렬 구현하기
자바스크립트에서 인접 행렬도 앞서 스택 & 큐와 마찬가지로 클래스를 이용하여 정의해볼 것이다. 클래스의 메소드는 정점 추가, 정점 존재여부 확인, 간선 추가, 간선 존재여부 확인, 간선 삭제 등을 구현할 것이다.
아래는 자바스크립트로 구현한 코드이다.
// directed graph (방향 그래프)
// unweighted (비가중치)
// adjacency matrix (인접 행렬)
// 이해를 돕기 위해 기존 배열의 인덱스를 정점으로 사용합니다 (0, 1, 2, ... --> 정점)
class GraphWithAdjacencyMatrix {
constructor() {
this.matrix = [];
}
addVertex() {
//버텍스를 추가합니다.
const currentLength = this.matrix.length;
for (let i = 0; i < currentLength; i++) {
this.matrix[i].push(0);
}
this.matrix.push(new Array(currentLength + 1).fill(0));
}
contains(vertex) {
//TODO: 버텍스가 있는지 확인합니다.
return vertex < this.matrix.length;
}
addEdge(from, to) {
const currentLength = this.matrix.length;
if (from === undefined || to === undefined) {
console.log("2개의 인자가 있어야 합니다.");
return;
}
//TODO: 간선을 추가할 수 없는 상황에서는 추가하지 말아야 합니다.
if (from + 1 > currentLength || to + 1 > currentLength || from < 0 || to < 0) {
console.log("범위가 매트릭스 밖에 있습니다.");
return;
}
//TODO: 간선을 추가해야 합니다.
this.matrix[from][to] = 1;
}
hasEdge(from, to) {
//TODO: 두 버텍스 사이에 간선이 있는지 확인합니다.
return this.matrix[from][to] === 1;
}
removeEdge(from, to) {
const currentLength = this.matrix.length;
if (from === undefined || to === undefined) {
console.log("2개의 인자가 있어야 합니다.");
return;
}
//TODO: 간선을 지울 수 없는 상황에서는 지우지 말아야 합니다.
if (from + 1 > currentLength || to + 1 > currentLength || from < 0 || to < 0) {
return;
}
//TODO: 간선을 지워야 합니다.
this.matrix[from][to] = 0;
}
}5. 인접 행렬을 이용하여 길찾기
앞서서 인접 행렬은 최단거리 찾기 문제를 해결하는데 최적화되어있다고 했다. 이번에는 한 정점에서 정점까지 이어진 길이 있는지(True or False)를 알아보는 코드를 작성할 것이다. 함수의 인자는 다음과 같다.
- 인자 1: matrix
Array 타입을 요소로 갖는 인접 행렬이 담긴 2차원 배열- 인자 2: from
Number 타입의 시작 정점- 인자 3: to
Number 타입의 도착 정점
문제 해결 방식은 아래와 같이 큐의 형식을 응용해볼 것이다.
const queue = [from];
const enqueue = n => queue.push(n);
const dequeue = n => queue.shift();그 다음에는 방문했는지를 알아보기 위한 1차원 배열을 생성할 것이다. 초기값은 false로 설정한다.
const isVisited = new Array(matrix.length).fill(false);그리고 from에 해당되는 인덱스는 출발지이기 때문에 이미 방문한 상태이다. 바꿔주자.
isVisited[from] = true;앞서 큐의 프린터문제와 마찬가지로 queue의 엘리먼트가 존재할 때 까지 반복한다.
while (queue.length > 0) {
}앞서 queue에서 추가했던 정점을 뺀다. 그 다음에 뺀 정점을 now로 저장한다.
만약에 now가 to랑 같다면(목적지 도착) 바로 true를 리턴하고 끝낸다.
만약에 목적지에 도착하지 않았다면 인접 행렬 matrix에서 now행을 선회한다.
matrix에서 now행의 element를 선회하는 도중에 간선이 존재하면서 방문하지 않은 곳을 발견하면, 다음 정점으로 가기 위하여 queue에 다음 정점을 기록해준다. 그리고 방문했음을 표시해준다.
위의 알고리즘은 아래와 같이 구현하면 된다.
const now = dequeue();
if (now === to) return true;
for (let next = 0; next < matrix[now].length; next++) {
if (matrix[now][next] && !isVisited[next]) {
enqueue(next);
isVisited[next] = true;
}
}그리고 위와 같은 과정을 반복했는데도 길이 안나온다면 false를 리턴해주면 된다.
아래는 최종 코드이다.
function getDirections(matrix, from, to) {
// queue를 간단하게 생성하고, 첫 시작점으로 from을 할당합니다.
const queue = [from];
const enqueue = (n) => queue.push(n);
const dequeue = (n) => queue.shift();
// 방문했다는 것을 표시하기 위해 1차원 행렬을 생성합니다.
const isVisited = new Array(matrix.length).fill(false);
// 첫 정점 방문 여부를 표시합니다.
isVisited[from] = true
// queue(방문할 곳)의 사이즈가 0이 될 때까지 반복합니다.
while (queue.length > 0) {
// queue에서 정점을 하나 빼서 now에 할당합니다.
const now = dequeue();
// 목적지인지 검사하고, 목적지라면 true를 반환합니다.
if (now === to) return true;
// 해당 정점의 간선들을 확인합니다.
for (let next = 0; next < matrix[now].length; next++) {
// 만약, 간선이 있고 방문하지 않았다면
if (matrix[now][next] && !isVisited[next]){
// queue에 next를 넣습니다. (다음 정점으로 가기 위해)
enqueue(next);
// 해당 정점을 방문했다는 것을 표시합니다.
isVisited[next] = true
}
}
}
// 길이 없다면 false를 반환합니다.
return false;
}