FFT(Fast Fouriere Transform)

FFT는 DFT(Discrete Fourier Transform)의 빠른 버전

DFT(Discrete Fourier Transform)

DFT는 이산 시간 영역의 신호를 이산 주파수 영역 표현으로 변환하는 역할을 합니다.

변환에 대해

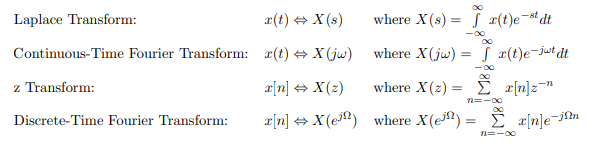
• Laplace Transform은 연속시간 신호 x(t)의 특성을 분석하기 위해 사용되는 변환 기술
  s평면에서 pole과 zero-응답을 찾기 위해 사용됩니다.

  pole 과 zero는 안정성, 응답 특성, 및 전반적인 동작을 나타냅니다.

• Z Transform은 이산시간신호 x[n]에서 pole과 zero를 찾기 위해 사용됩니다.

• Continuous-Fourier Transform(CTFT,연속 시간 푸리에 변환) 은 Laplace Transform s = jω로 나타내면 얻을 수 있습니다. 이 를 통해 연속 시간 신호의 주파수 도메인 특성을 파악할 수 있습니다.
  Discrete-Time Fourier Transform(DTFT,이산 시간 푸리에 변환)은 Z변환을 z = e^jΩ로 나타내면 얻을 수 있습니다. TFT를 통해 이산 시간 신호의 주파수 도메인 정보를 파악할 수 있습니다.

DFT 와 DTFT?

두 변환 모두 이산 시간 신호로 시작하지만, DTFT는 주파수 영역에서 연속적이고 DFT는 이산 주파수 영역 표현을 생성함.

• 주기성: DTFT인 X(e^jΩ)는 주기적. 주기는 f = 0부터 fs까지로, 여기서 fs는 샘플링 주파수를 나타냅니다. 이 중복성을 활용하여 DFT는 0과 fs 사이의 영역에서만 정의됨.

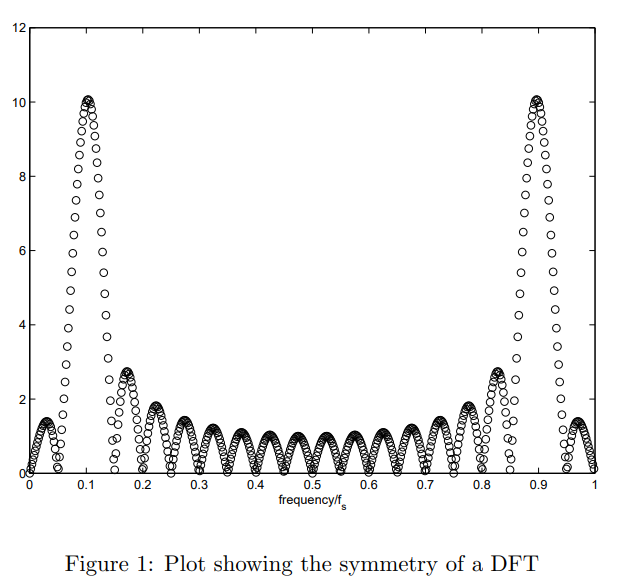
• 대칭성: 0부터 fs 사이의 영역을 살펴보면 중심점인 0.5fs, 나인퀴스트 주파수 기준으로 대칭. 아래 그림은 샘플링 주파수의 10분의 1 주파수를 가지는 코사인의 DFT(Matlab의 FFT 함수를 사용하여 구현)를 보여줍니다. 0.5fs와 fs 사이의 데이터가 0과 0.5fs 사이의 데이터와 대칭입니다.

fs(sampling frequency or sampling rate)

1초에 측정되는 데이터의 개수. 0.1 초 간격으로 데이터를 측정하면 10 Hz가 샘플링 주파수 fs가 된다. fs는 FFT 결과에서 최대 주파수를 정한다. fs가 10 Hz 이면 0~5 Hz 의 결과와 5~10 Hz의 결과가 동일하여 0~5 Hz의 결과만 보면 된다. fs의 반 5Hz 를 Nyquist 주파수라고 한다. 이렇게 FFT 결과는 나이키스트 주파수에 대해서 대칭성을 가지게 된다.

FFT와 Matlab을 사용한 스펙트럼 분석

• FFT의 포인트 수(N) 및 표현된 신호의 주기 수에 따라 크게 변할 수 있습니다.

• FFT에는 0부터 fs까지의 정보가 포함되어 있지만, 샘플링 주파수는 최고 주파수 성분의 두 배 이상이어야 합니다.
  따라서 신호의 스펙트럼은 fs/2, 나인퀴스트 주파수 아래에 있어야 합니다.

• 실제 신호는 양수와 음수 주파수에 대해 대칭적인 변환 크기를 가져야 합니다. 따라서 0부터 fs까지의 스펙트럼을 가지는 대신에 -fs/2부터 fs/2까지의 스펙트럼을 표시하는 것이 더 적절합니다.

  이를 위해 Matlab의 fftshift 함수를 사용할 수 있으며, 아래의 코드가 이를 보여줍니다.

 n = [0:149];
x1 = cos(2*pi*n/10);
N = 2048;
X = abs(fft(x1,N));
X = fftshift(X);
F = [-N/2:N/2-1]/N;
plot(F,X),
xlabel('frequency / fs')

참고문헌
http://www.phys.nsu.ru/cherk/fft.pdf
https://kr.mathworks.com/help/matlab/ref/fft.html