Gradient descent

gradient descent는 선형 회귀의 비용 함수뿐만 아니라 어떤 함수든 최소화하기 위해 사용할 수 있는 알고리즘입니다.

gradient descent는 두 개 이상의 매개 변수를 가진 모델에서도 작동하는 다른 비용 함수에 적용할 수 있습니다. 예를 들어, 비용 함수 J이 w_1부터 w_n까지의 매개 변수와 b의 함수인 경우, 목표는 매개 변수 w_1부터 w_n과 b에 대한 j을 최소화하는 것입니다. 즉, 가장 작은 j 값을 제공하는 w_1부터 w_n과 b의 값을 선택하려는 것입니다. Gradient descent는 이 비용 함수 j을 최소화하기 위해 적용할 수 있는 알고리즘입니다.

Gradient descent 알고리즘을 사용하려면 먼저 w와 b에 대한 초기 추측값을 설정해야 합니다. 선형 회귀의 경우 초기 값이 크게 중요하지 않습니다. 일반적인 선택은 w와 b를 모두 0으로 설정하는 것입니다. 예를 들어, w를 0으로, b를 0으로 초기 추측값으로 설정할 수 있습니다. Gradient descent 알고리즘을 사용하면 매개 변수 w와 b를 조금씩 변경하여 비용 j(w, b)를 줄이려고 할 것입니다. 이렇게 하면 비용 j이 최소화되거나 근처의 값으로 수렴하게 될 것입니다.

한 가지 주의할 점은 j 함수에 따라 보편적인 볼록한 모양이 아닐 수 있다는 것입니다. 또 다른 가능한 최소값이 여러 개 있는 경우도 있습니다.
이제 더 복잡한 표면 플롯 j 예제를 살펴보며 gradient descent가 어떤 작업을 수행하는지 이해해 보겠습니다.

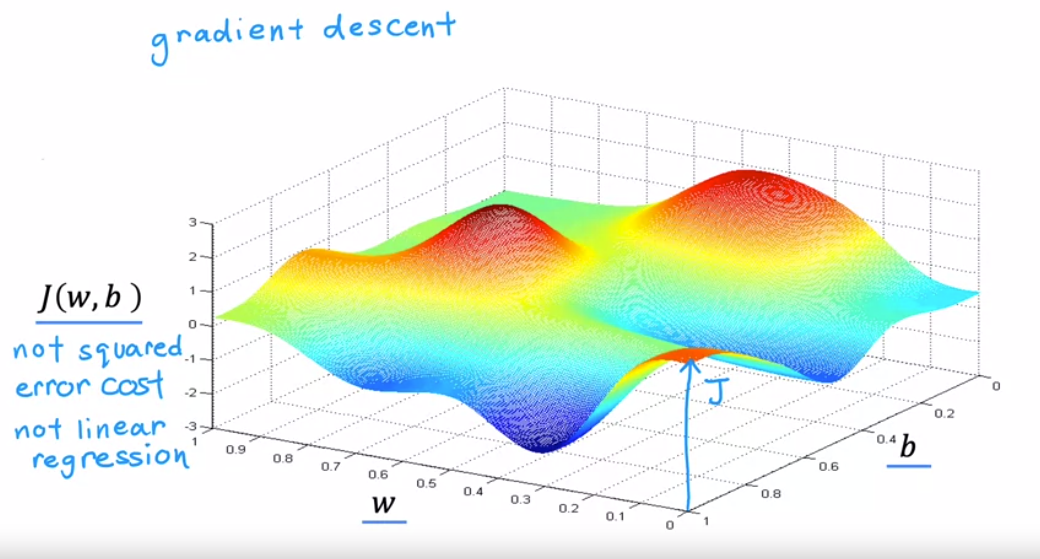
x 축은 w와 b를 나타냅니다. 다양한 w와 b 값에 대해 서로 다른 지점들이 나타나며, 각 지점의 높이가 비용 함수의 값입니다.
Gradient descent 알고리즘은 360도 돌아보며 자신에게 다음 작은 걸음을 어느 방향으로 내려가기 위해 선택할 것인지 물어봅니다. 가능한 한 빠르게 내리기 위한 최상의 방향은 수학적으로는 가장 가파른 하강 방향입니다.

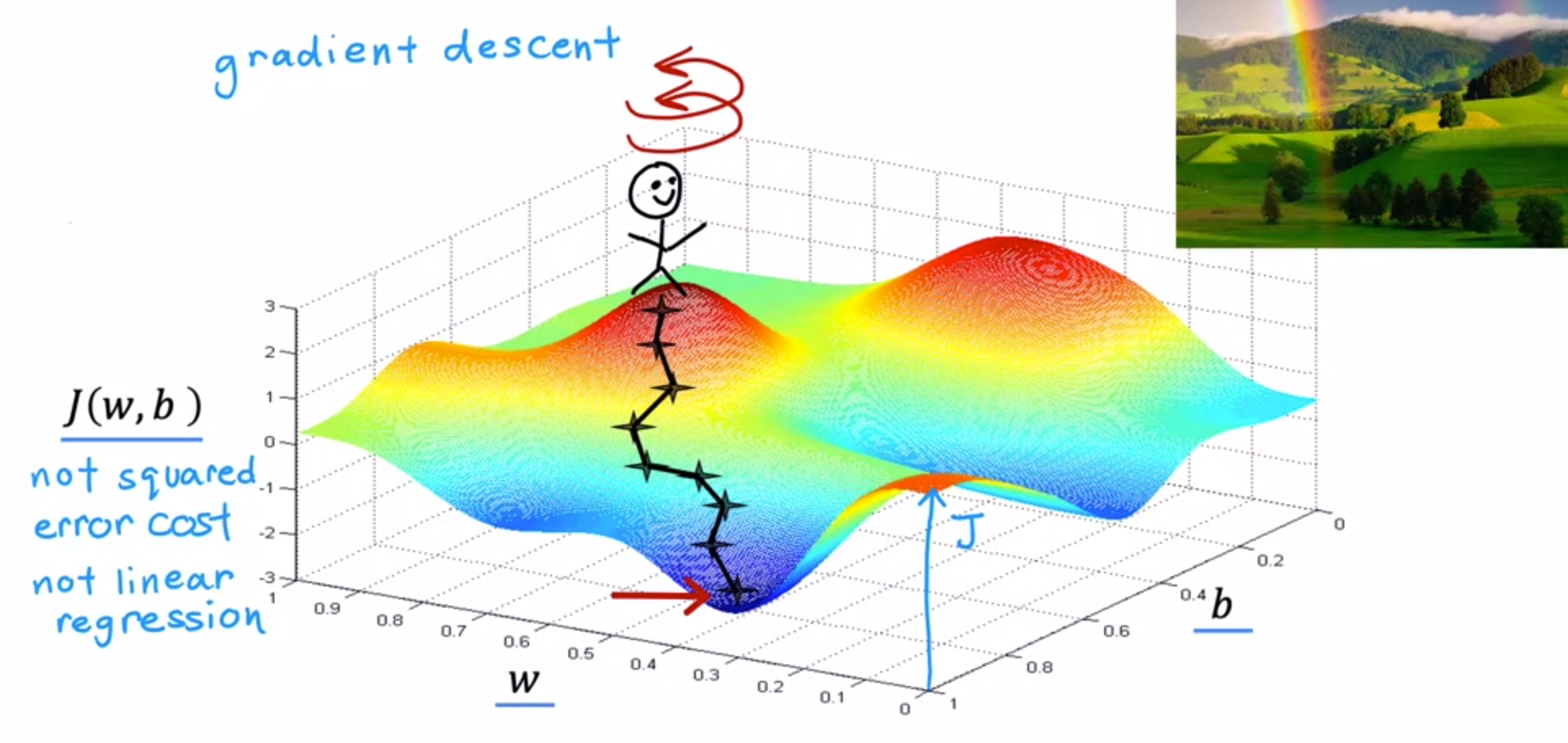
이렇게 반복하여 이 계곡의 밑바닥에 도달하게 됩니다. 여기서 진행한 것은 gradient descent의 여러 단계입니다. Gradient descent의 흥미로운 특징 중 하나는 시작점을 선택할 때 매개 변수 w와 b의 초기 값을 선택할 수 있다는 것입니다.
방금 수행한 gradient descent에서는 이 지점에서 시작했습니다. 이제 두 번째로 gradient descent를 실행하되 처음에 첫 번째 시도 때보다 오른쪽으로 몇 걸음 떨어진 곳에서 시작하겠습니다. 그런 다음 gradient descent 과정을 다시 반복합니다.

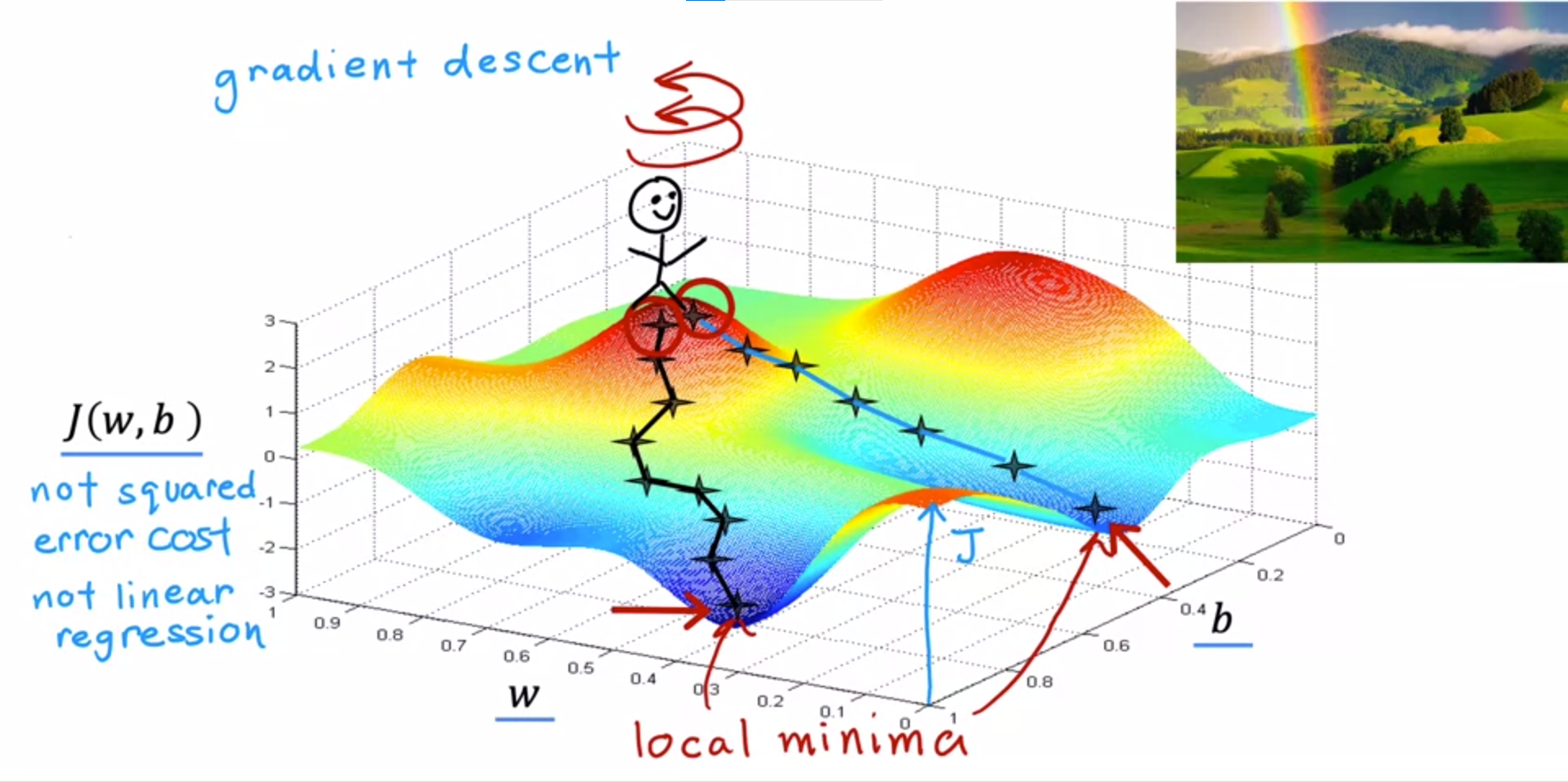
이렇게 하면 첫 번째 시도 때보다 오른쪽으로 몇 걸음 떨어진 곳에서 시작하여 오른쪽의 다른 계곡에 도달하게 됩니다. 첫 번째와 두 번째 계곡의 바닥은 지역 최솟값(local minimum)이라고 합니다. 이것은 gradient descent 알고리즘의 흥미로운 특징입니다.

• α(learning rate) 보통 0과 1 사이의 작은 양수 값(예: 0.01)입니다. 알파는 기본적으로 얼마나 크게 하강하는지를 제어합니다. 알파가 크면 큰 경사 하강을 의미하며 반면, 알파가 작으면 작게 하강 합니다.
• d/dw of J(Derivative) 일단은 이 미분 항을 현재 위치에서 어느 방향으로 이동해야 하는지를 나타내주는 것으로 생각할 수 있습니다. learning rate 알파와 함께 사용되어 내려가는 크기도 결정합니다.
  

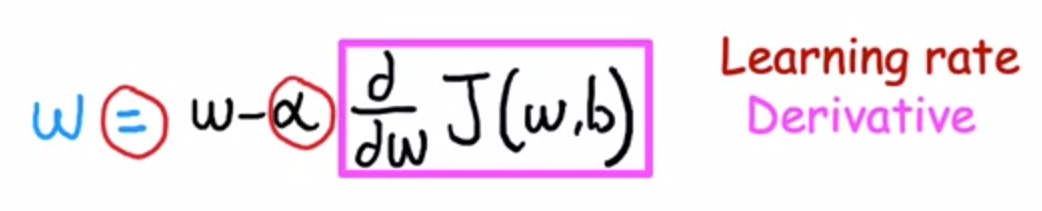
tmp_w가 tmp_b에 영향을 미치므로 수식이 정확하지 않습니다.