[딥러닝CV] 4. 3-Channel Convolution

[딥러닝CV] 목차

1. 컴퓨터 비전 태스트 '상상'해 보기
2. 다층 퍼셉트론(Multi-Layer Perceptron) 구조 복습하기
3. CNN 하나씩 이해하기 (1) 1-Channel Convolution
   4. CNN 하나씩 이해하기 (2) 3-Channel Convolution
4. CNN 하나씩 이해하기 (3) Pooling
5. 심화된 CNN 구조
6. Transfer Learning 이해하기
7. Object Detection
8. Segmentation

1. Channel이 3개일 때, 1-Layer의 Convolution 연산

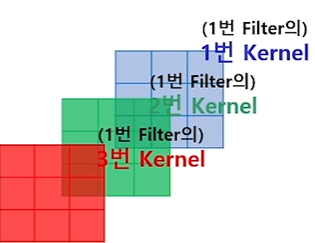
필터가 커널의 상위 개념

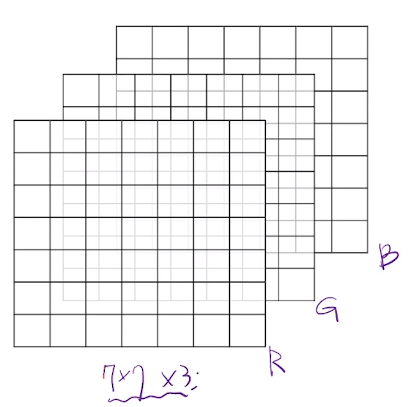
Q. 7 x 7 x 3의 input에 3x3의 kernel, stride 1인 Convolution 연산을 하면 output의 크기는 어떻게 되나요? feature map의 크기는 어떻게 되나요?

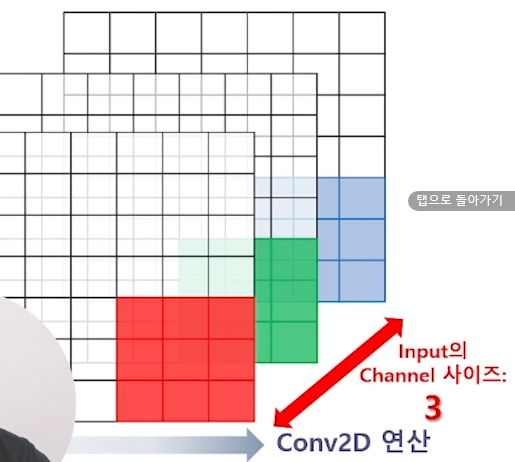
kernel은 input의 channel 수만큼 존재하고,
각 channel 수준에서 Convolution 2D 연산을 계속하면
channel 수만큼의 output이 생깁니다.
따라서 output은 5 x 5 x 3(channel) 이 나옵니다.

filter 1개로 feature map 1개를 만들 수 있습니다.
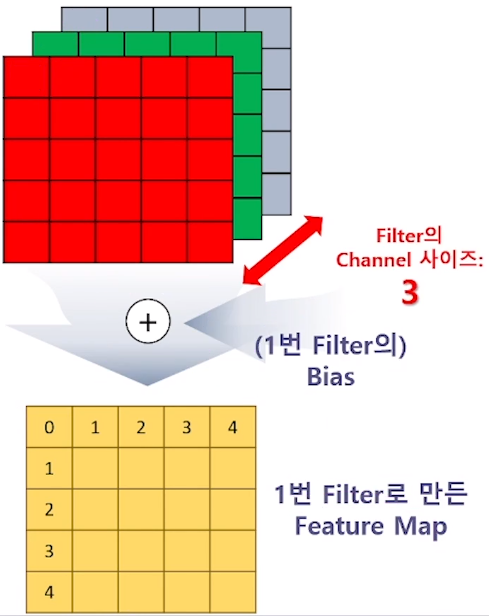
3개의 output의 동일한 위치의 숫자를 더하고
거기에 1번 filter의 bias를 더하여
1번 filter의 5 x 5 feature map을 만들 수 있습니다.
즉 “(5 x 5) x 3”개의 칸에 같은 값(bias)이 더해져 feature map을 만듭니다.

Q. filter마다 위의 연산과정을 반복하게 됩니다. filter은 어떤 역할을 하고 filter가 많으면 어떻게 되는지 설명해 보세요.

참고) filter 안에는 3개(R,G,B)의 kernel(3X3)가 있다.
복습) kernel은 stride 숫자간격에 따라 overriding 하는 것
filter = Feature Extractor (Feature=pattern 을 찾아내는 역할)

즉, filter 개수가 많아질수록 Feature=pattern을 더 잘 찾아내게 된다. (우리가 원하는 바)

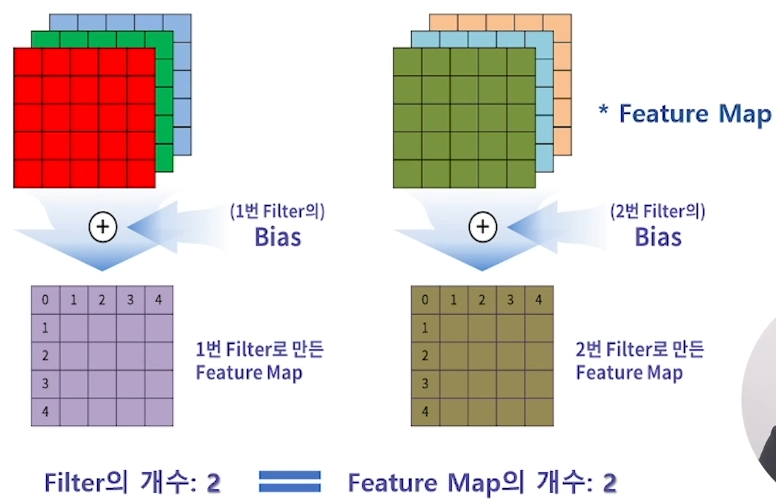
(Feature Map = Activation Map)

Q. input의 channel 수, feature map의 channel 수, filter의 개수의 관계에 대해서 설명해 보세요.

input의 channel 수 =! feature map의 channel 수
filter의 개수 = feature map의 channel 수

filter 하나로 Feature Map 하나가 나온다!

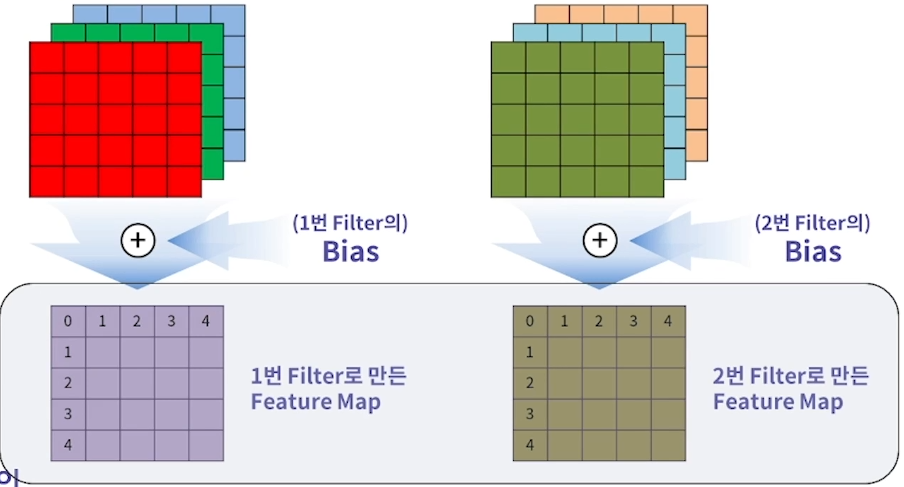
Convolutional Neural Network(CNN)에서의 입력 이미지와 특징 맵(feature map) 사이의 채널 수가 다를 수 있는 이유는 다음과 같습니다:

입력 이미지의 채널 수
: 이미지의 입력 채널 수는 주로 원본 이미지의 특성을 나타냅니다. RGB 이미지의 경우 3개의 채널(R, G, B)이 있습니다.

합성곱 필터의 개수
: CNN에서는 여러 개의 필터를 사용하여 이미지의 다양한 특징을 감지합니다. 이러한 필터는 서로 다른 특징이나 패턴을 찾기 위해 학습됩니다. 이때, 각 필터마다 출력되는 특징 맵(feature map)은 필터의 개수와 같은 채널 수를 갖습니다. 따라서 여러 필터를 사용하면 특징 맵의 채널 수가 늘어날 수 있습니다.

풀링 레이어와 함께하는 차원 축소
: 풀링(pooling) 레이어는 특징 맵의 공간적인 차원을 축소하는 데 사용됩니다. 이 과정에서 채널 수는 변하지 않을 수 있습니다.

따라서 입력 이미지와 특징 맵의 채널 수가 같지 않을 수 있는 이유는 CNN에서 여러 개의 필터를 사용하고, 각 필터마다 다양한 특징을 추출하여 특징 맵을 생성하기 때문입니다. 이를 통해 다양한 시각적 특징을 학습하고 나타낼 수 있습니다.

2. Hyper-Parameter에 대한 고민

(Kernel size, Channel size, Stride)
Convolution 연산을 할 때, Hyper-Parameter에 대한 고민을 해야 합니다.

2-1. Kernel Size

Kernel size가 커질수록 연산을 통해 찾아야 하는 파라미터의 수가 증가하게 됩니다.
Kernel size가 작아질수록 데이터에 존재하는 global feature보다 local feature에 집중하게 됩니다. 쉽게 표현하자면 큼직한 특징보다는 지엽적인 특징에 집중해서 패턴을 찾게 됩니다.

2-2. Channel size

Filter의 channel size가 커질수록 convolution 연산을 통해서 더 다양한 패턴을 찾을 수 있습니다.
그러나 channel의 사이즈가 커짐에 따라서 연산으로 찾아야 하는 파라미터의 숫자가 증가하게 됩니다.

2-3. Stride

Stride 값이 커지면 데이터를 빠르게 훑고 지나가는 연산을 하게 됩니다.
따라서 지역적인 특징을 꼼꼼하게 살펴보아야 할 경우에는 stride값을 크게 하는 것이 좋지 않습니다.

안타깝게도 이러한 hyperparameter의 값을 어떻게 정하는 것이 최적이라는 규칙을 찾는 것은 매우 어려운 일입니다. 따라서 연구자는 시행착오를 스스로의 실습으로 해거나 AutoML과 같은 방법으로 hyperparameter를 스스로 tuning해야 합니다.

AutoML은 머신러닝과 딥러닝을 적용할 때마다 반복적인 과정으로 발생하는 비효율적인 작업(하이퍼 파라미터 실험, 문제 적합한 architecture를 찾는 과정 등)을 최대한 자동화하여 생산성과 효율을 높이기 위하여 등장한 것으로, 현재 다양한 툴들이 개발되어 있습니다.

Q. Convolution 연산을 할 때와 모델을 학습할 때에는 다양한 hyperparameter의 값을 정해야 합니다. hyperparameter와 많이 혼용해서 사용되는 개념인 매개변수 parameter에 대해서 알아봅시다. 각각의 개념을 찾아보고 두 개념의 차이점에 대해서 설명해 보세요.

파라미터와 하이퍼파라미터 모두 매개변수(parameter)이지만,
두 개념은 차이점이 있습니다.

매개변수(Parameters):
모델이 학습하는 동안 (데이터로부터) 조정하는 변수로서
weight coefficient(가중치 계수), bias(편향치)가 해당된다.

모델이 데이터에 대한 패턴을 학습하고 예측을 수행합니다.
모델의 예측에 직접적으로 영향을 준다.

하이퍼파라미터(Hyperparameters):
(사람으로부터) 사전에 정의되는 변수로서
학습률(learning rate), 에포크 수(epoch), batch size, 정규화에 사용되는 가중치 등이 해당된다.

이 값들은 모델 구성, 학습 속도, 학습 알고리즘 등을 조절하여
모델의 성능을 개선하는 데 간접적으로 영향을 줄 수 있다.

간단히 말하면, 매개변수는 모델이 학습하는 동안 업데이트되는 값,
하이퍼파라미터는 모델의 구조나 학습 과정을 제어하는데 사용되는 사전에 정의된 값

3. 1x1 Convolution

Convolution 학습을 수행하는 layer를 사용해서 원하는 모델을 구성할 때는 Filter의 Channel 수를 직접 결정해야 합니다. 이전에 언급한 대로, 일반적으로는 좋은 성능을 보이는 논문에서의 구조를 그대로 따라하지만, 때로는 연구자가 직접 결정해주어야 합니다.

channel size가 지나치게 크면 학습을 통해 찾아야 하는 파라미터 숫자가 증가하기 때문에 많은 연산 비용을 들여야만 합니다. 하지만 1x1 Convolution을 사용하면 연산량을 매우 쉽게 줄일 수 있습니다.

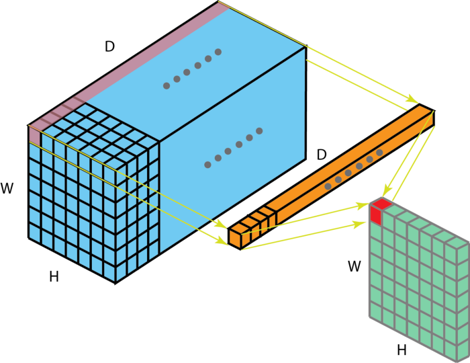
때로는 feature map의 가로 세로 사이즈는 변화시키지 않고 channel size만 변형하고 싶을 때가 있습니다. 물론 padding을 통하여 가로 세로 사이즈에 대한 변경없이 channel size만 변경할 수 있지만 파라미터 숫자 증가에 따른 연산량 증가의 문제를 피할 수 없습니다. 이럴 때 1x1 convolution은 연산량의 문제를 회피하면서도 channel size를 원하는 대로 변경하는 데에 도움을 줍니다.

Q. 1x1 Convolution을 사용하면 연산량을 매우 쉽게 줄일 수 있습니다.
계산량이 실제로 줄어드는지 예시 2개를 풀어보고, 두 개의 값을 비교하여 생각해 보세요.

[예시 1] 28x28x192 image 데이터에 (5x5 filter, 32 channel) convolution 연산을 적용한다고 해 봅시다.
이때, feature map의 크기와 파라미터 수에 대해서 생각해 보세요.

[예시 2] 28x28x192 image 데이터에 (1x1 filter, 16 channel) convolution 연산을 사용하여 channel을 줄인 뒤,
이어서 (5x5 filter, 32 channel) convolution 연산을 적용 한다고 해 봅시다.
이때, feature map의 크기와 파라미터 수에 대해서 생각해 보세요.

예시 1의 feature map의 크기는 24x24x32가 나옵니다. 파라미터 수(연산량)는 28 x 28 x 32 x 5 x 5 x 192 = 120,422,400 약 1.2억 번의 연산이 필요합니다.

예시 2의 feature map의 크기도 24x24x32가 나옵니다. 먼저, 1x1 filter를 사용해서 크기를 줄일 때 사용되는 파라미터 수(연산량)는 28 x 28 x 16 x 1 x 1 x 192 = 2,408,448 약 240만 번의 연산이 필요합니다. 다시 5x5 filter를 사용하면 28 x 28 x 32 x 5 x 5 x 16 = 10,035,200 약 1000만 번의 연산이 필요합니다. 그럼 총 약 1240만 번의 연산이 필요합니다.

예시 1과 예시 2의 파라미터 수(연산량)는 1.2억 번(12000만 번) 과 1240만 번의 연산으로 10배 가까이 차이 나는 것을 확인할 수 있습니다. 실제로 1x1 convolution은 연산량의 문제를 회피하면서도 channel size를 원하는 대로 변경하는 데에 도움을 줍니다. 직접 수치로 비교하니 더 이해가 잘 되지 않나요? 🤔😉

4. Transposed Convolution

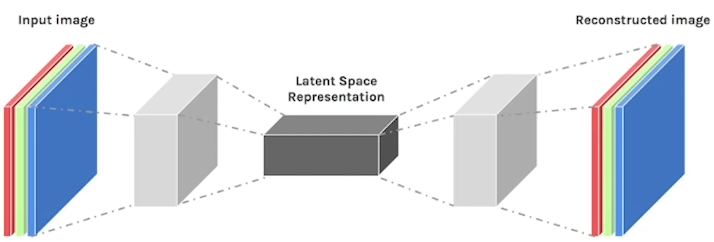
Auto-Encoder 구조에서 입력 정보가 압축된 compressed representation 을
다시 원래 입력 사이즈로 반환하기 위해 사용한다.

정보를 축약하는 down-sampling 이라는 표현과 반대로 up-sampling 한다고 말하기도 한다.

Low-resolution의 이미지를 high-resolution으로 바꾸는 역할도 할 수 있다.

Q. Transposed Convolution을 사용하는 이유와 특징에 대해서 설명해 보세요.

Transposed Convolution은 Auto-Encoder 구조에서 입력 정보가 압축된 compressed representation을
다시 원래 입력 사이즈로 반환하기 위해 사용합니다.
정보를 축약하는 down-sampling이라는 표현과 반대로 up-sampling 한다고 말하기도 합니다.
Low-resolution의 이미지를 high-resolution으로 바꾸는 역할도 할 수 있고,
Pixel 별로 할당된 정답 값을 맞추는 task인 semantic segmentation에서도 활용할 수 있습니다.

Q. 아래 조건을 보고 Transposed Convolution 연산이 어떻게 진행되는지 Convolution 연산과 어떤 차이점이 있는지 직접 손으로 그려서 확인해 보세요.

• Input: 4 x 4
• kernel: 3 x 3
• Output: 6 x 6
• stride: 1

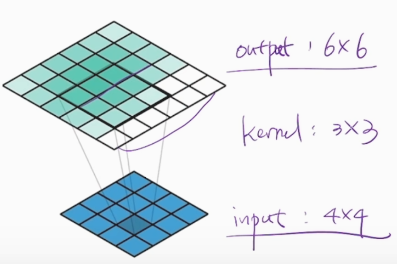
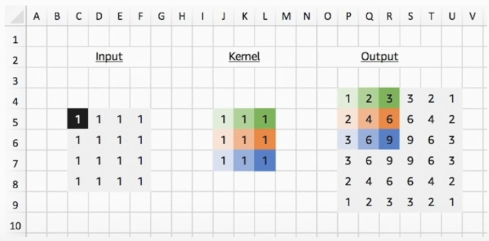
Transposed Convolution 연산이 Convolution 연산과 다른 점은

1. 결과 크기
   컨볼루션 연산의 결과는 입력 크기보다 작은 출력 크기를 갖는다. (stride, padding에 따라 달라질 수 있음)
   트랜스포즈드 컨볼루션의 결과는 입력 크기보다 큰 출력 크기를 갖는다. (업샘플링을 통해 입력보다 큰 영역을 포함하는 결과가 생성되기 때문)

2. 적용 분야
   일반적인 컨볼루션은 다운샘플링을 통해 특징을 추출하여 인코더 부분에서 사용되며,
   이미지 분류, 객체 검출, 특징 추출 등에 주로 활용
   트랜스포즈드 컨볼루션은 보통 디코더 부분에서 업샘플링을 위해 사용되며,
   이미지 복원, 분할, 슈퍼 해상도, 생성 모델 등에서 활용

   Encode: 압축화, 코드화
   Decode: 암호해제 (압축했던 것을 다시 풀어헤친다)

3. 컨볼루션 연산과 트랜스포즈드 컨볼루션 모두 가중치 파라미터를 갖고 있지만
   컨볼루션 연산은 입력 데이터의 특징을 추출하기 위해 가중치를 학습하고,
   트랜스포즈드 컨볼루션은 업샘플링을 위한 가중치를 학습.

4. 업샘플링과 다운샘플링
   일반적인 컨볼루션 연산은 다운샘플링을 통해 입력 데이터의 공간적인 차원을 줄인다.
   트랜스포즈드 컨볼루션은 업샘플링을 수행하여 출력 데이터의 크기를 키운다.

Q. 7x7x3 image의 데이터에 5x5x3의 필터 5개로 convolution 연산을 했을 때 feature map의 사이즈는 어떻게 되나요? (stride는 1)

Q. 7x7x3 image의 데이터에 5x5x3의 필터 3개로 convolution 연산을 했을 때 feature map의 사이즈는 어떻게 되나요? (stride는 2)

Q. 9x9x3 image의 데이터를 3x3xn의 필터 4개로 convolution 연산을 두 번 했을 때, 연산의 결과로 나온 최종 feature map의 사이즈는 어떻게 되나요? (stride는 처음에는 1, 두번째에는 2, n은 입력 데이터의 채널 수와 같습니다.)

마무리

Q. Convolution 연산은 어떤 연산인지 설명해 보세요.

이미지 내의 패턴을 자동으로 추출하는 Filter(그 안의 Kernel)를 이용해서 숨겨진 패턴을 찾는 연산