Javascript를 배우고 있는 예비 개발자입니다.
오늘 배운 내용을 간단히 정리하고자 합니다.
수정사항이 있을시 알려주시면 적극적으로 배우겠습니다.
What I leaned today :)
😆 Graph
😆 Tree (Binary tree) 📌⭐︎ Tree
Tree(트리)구조는 Graph의 종류 중 하나로 구분이 된다.
다만, Graph는 이전 포스트에서 볼 수 있듯이 뭔가 평등?한 사회적 그림이 그려진다면
Tree구조는 전형적인 계층구조의 그림을 그릴 수 있다.
실제로 Tree 구조가 가지고 있는 node는 Parent & child를 가지고 있는데
최상위 노드(root)가 제일 상석에서 왕처럼 군림하고 있고, 그 root 노드 아래 child가,
그 child 아래에 또 child가 있는 구조를 생각하면 된다.
그냥 관료제형 피라미드 구조를 떠올리면 편하다.
아래 사진을 보도록 하자.
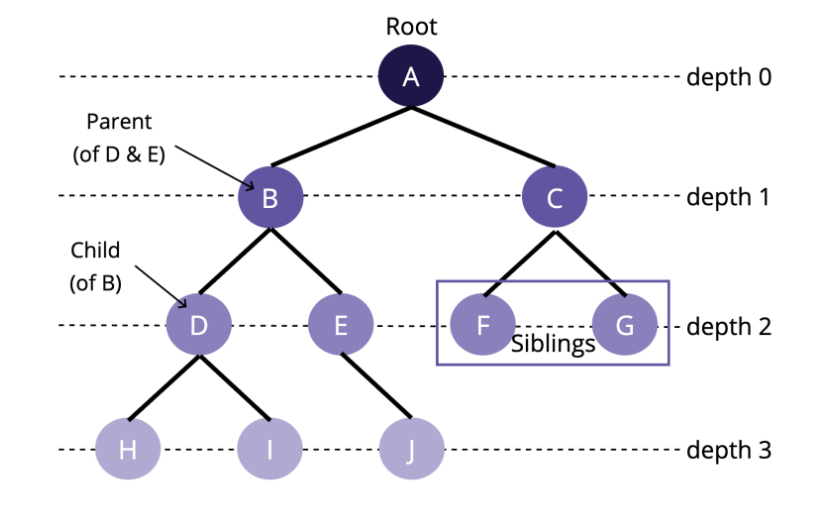
☀️ 반드시 알아야 할 개념!
part 1
-
A, B, C, D 등 트리의 구성요소를 노드(node)라고 부른다.
-
위의 그림 A처럼, 트리 구조에서 최상위에 존재하는 node를 root라고 한다.
-
루트를 기준으로, 다른 노드로의 접근하기 위한 거리를 Depth라고 한다.
-
같은 부모를 가지면서 같은 depth에 존재하는 노드들은 Sibling관계에 있다.
-
그림에서 A는 B와 C의 부모(Parent)이고, B와 C는 A의 자식(Child)이다.
-
노드와 노드를 잇는 선을 edge라고 한다. ( = link, branch)
-
자식이 없는 노드는 단말노드 혹은 leaf라고 한다. (H, I, J, F, G)
(참고 내부(internal)노드는 리프노드가 아닌 노드를 지칭)참고: 코드스테이츠
part 2
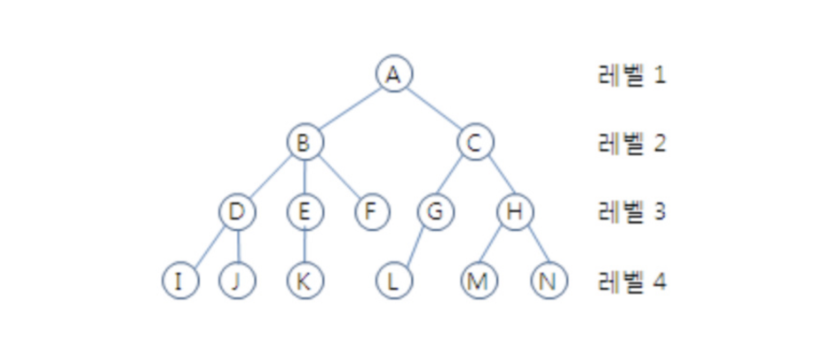
- 노드의 크기(size) : 자신을 포함한 모든 자손 노드의 개수.
->C의 크기 :6 - 노드의 깊이(depth) : 루트에서 어떤 노드에 도달하기 위해 거쳐야 하는 간선의 수
->D의 깊이 :2
->L의 깊이 :3 - 노드의 레벨(level) : 트리의 특정 깊이를 가지는 노드의
집합
->A의 레벨 :1
->B,C의 레벨 :2
->D,E,F,G,H의 레벨 :3 - 노드의 차수(degree) : 부(하위) 트리 갯수/간선수 (degree) = 각 노드가 지닌 가지의 수
->A의 차수 =2
->B의 차수 =3
->C의 차수 =2 - 트리의 차수(degree of tree) : 트리의 최대 차수
->B가 최대 차수를 가짐 =>3 - 트리의 높이(height) : 루트 노드에서 가장 깊숙히 있는 노드의
깊이
->3
주의!! Tree의 Depth 와 Height를 꼭 비교하고 가자!!
☀️ Binary Tree
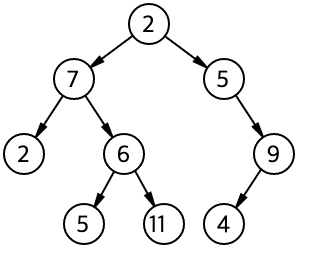
Binary Tree는 이진 트리라고도 불리며,
각각의 노드가 최대 두 개의 자식 노드를 가지는 트리 자료 구조로, 자식 노드를 각각 왼쪽 자식 노드와 오른쪽 자식 노드라고 한다.
트리구조는 재귀적인 성질을 가지고 있고, 자식 노드 역시 최대 2개의 자식을 갖는다.
막간을 이용하는 Potter's 영한 사전 😎
Birnary란?
2진수의; '두 부분으로 이뤄진', 2항의Part 1
정 이진 트리 (Full Binary Tree)
leaf를 제외한 모든 노드가 0개 || 2개의 자식 노드를 가지고 있다.
포화 이진 트리(perfect binary tree)
모든 노드가 0개 || 2개의 자식노드를 가지며 모든 리프노드가 똑같은 레벨에 있는 경우의 트리이다.
(정 이진 트리의 상위 개념)
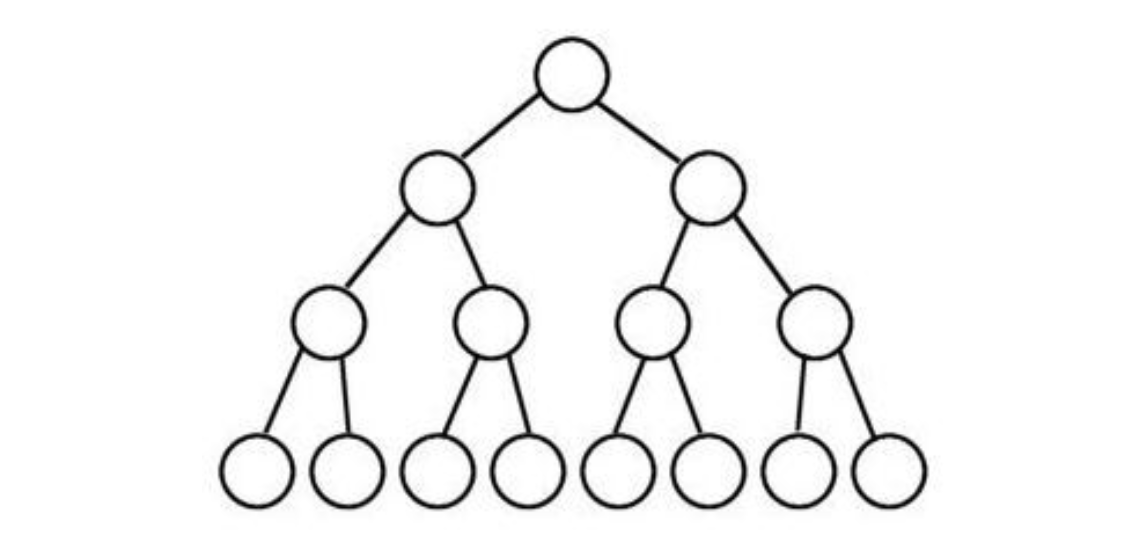
완전 이진 트리(complete binary tree)
왼쪽 자식노드부터 채워지며
마지막 레벨을 제외하고는 모든 자식노드가 채워져있는 트리이다.
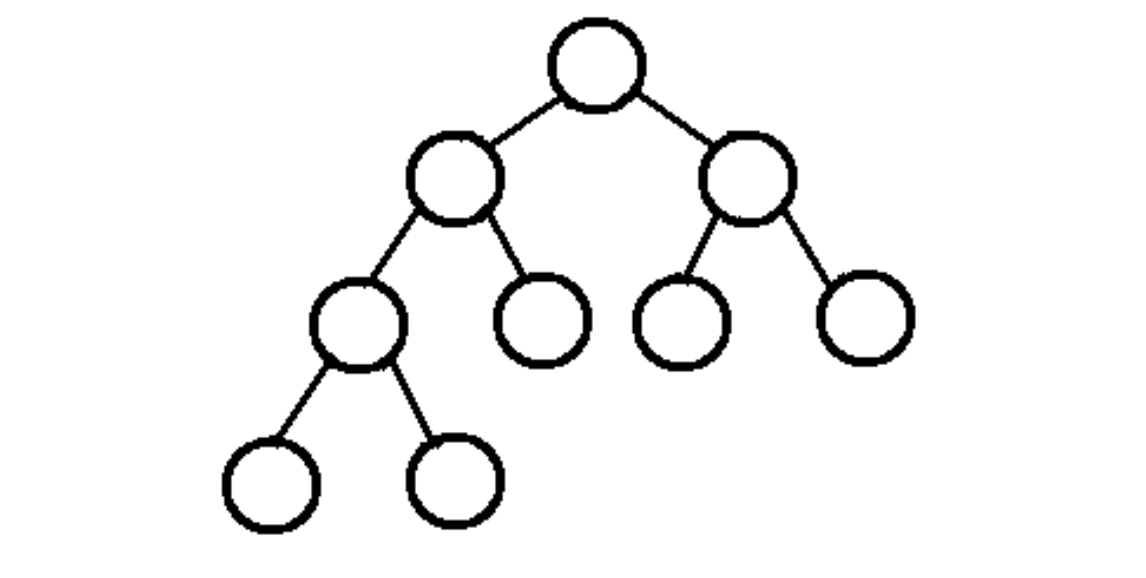
편향 이진 트리(skewed binary tree)
말 그대로 노드들이 전부 한 방향으로 편향된 트리이다.
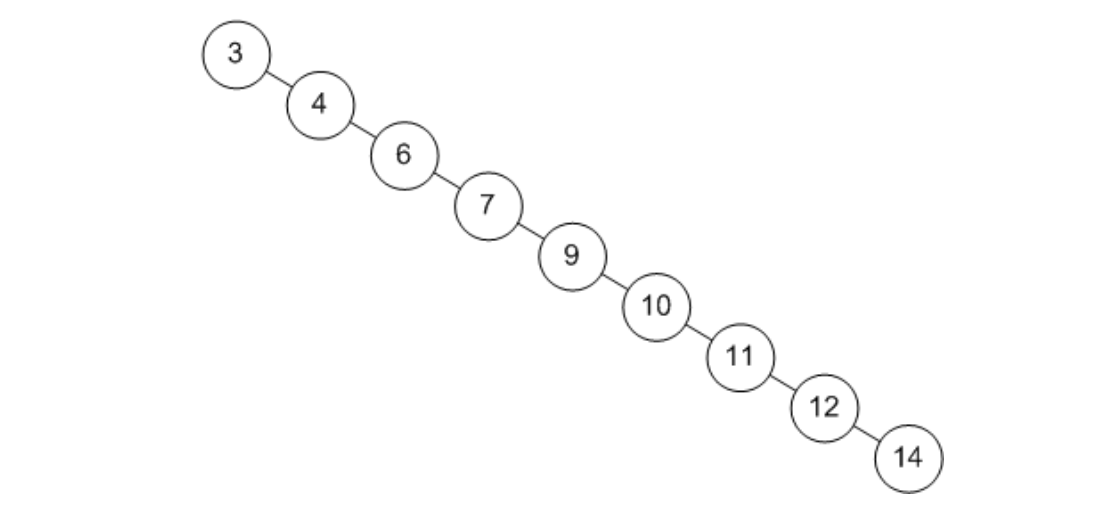
Part 2
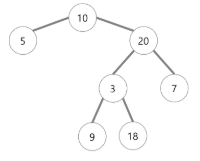
☀️ Binary Search Tree (이진 탐색 트리)
Binary Search Tree는 Binary Tree 종류 중 하나이다.
하지만 그 어떤 종류보다 이 이진 탐색 트리를 자주 만나게 된다고 하니 꼭 기억하도록 하자.
노드의 값이 정렬 방법에 따라 순서가 존재한다.
노드의 왼쪽 서브트리에는 노드의 값도자 작은 값,
오른쪽 서브트리에는 노드의 값보다 같거나 큰 값이 존재한다.
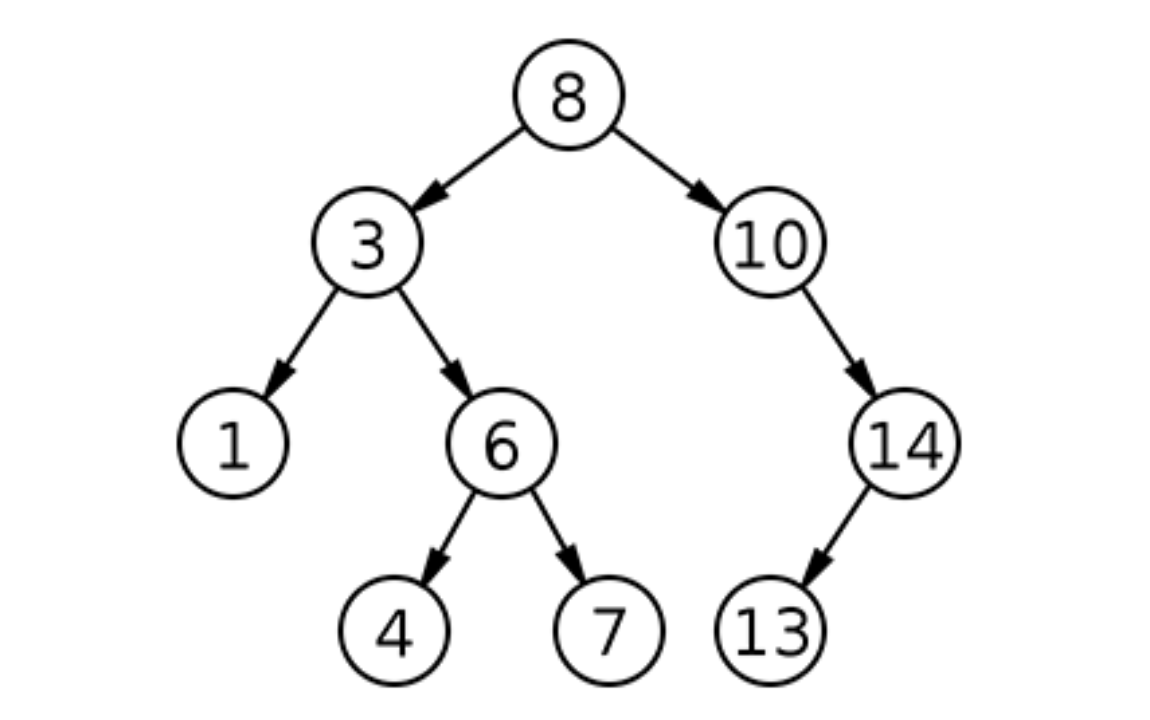
이진 탐색 트리 순회 방식
위와 같은 이진 탐색 트리 내부에 있는 특정 노드들을 건드리고자 할 때
트리를 순회하면서 특정 노드를 찾아야하는데 3가지 방식이 있다.
-
전위 순회(Preorder Traversal): 부모 → 좌 → 우
-
중위 순회(Inorder Traversal): 좌 → 부모 → 우
-
후위 순회(Postorder Traversal): 좌 → 우 → 부모
이러한 과정은 재귀로 쉽게 설명할 수 있다.
정리
-
이진트리 (binary tree)
child node가 최대 2개까지만 붙는 것
-
이진탐색트리 (binary search tree) : 순서를 갖는다.
왼쪽: child node는 node 보다 작음
오른쪽: child node가 큼
어떤 개발자의 말을 인용하자면,
Binary Search Tree는 마치 Up-down 게임과 같다고 한다.
트리의 밸런스를 맞추기 위한 트리 재구성을 할 때 업다운게임의 방식과 유사해서인데
이는 조금만 더 공부하고 포스팅을 추가적으로 하겠다.끝!

