[BOJ, Python] 1005번_ACM Craft

백준 1005번

얼핏 보기에는 쉬워보였다. 조금 헷갈리긴 했지만 결국 그래프탐색 문제이고, 출발점을 어디로 잡는지만 결정한다면 문제를 쉽게 풀릴 것이라고 생각했다.
그래서 역발상으로 출발점을 목표 건물로 잡고 BFS를 해서 문제를 풀고자 했다.

당연히 테스트는 실패했다. 일반적인 bfs로 풀 시 문제점이 있다
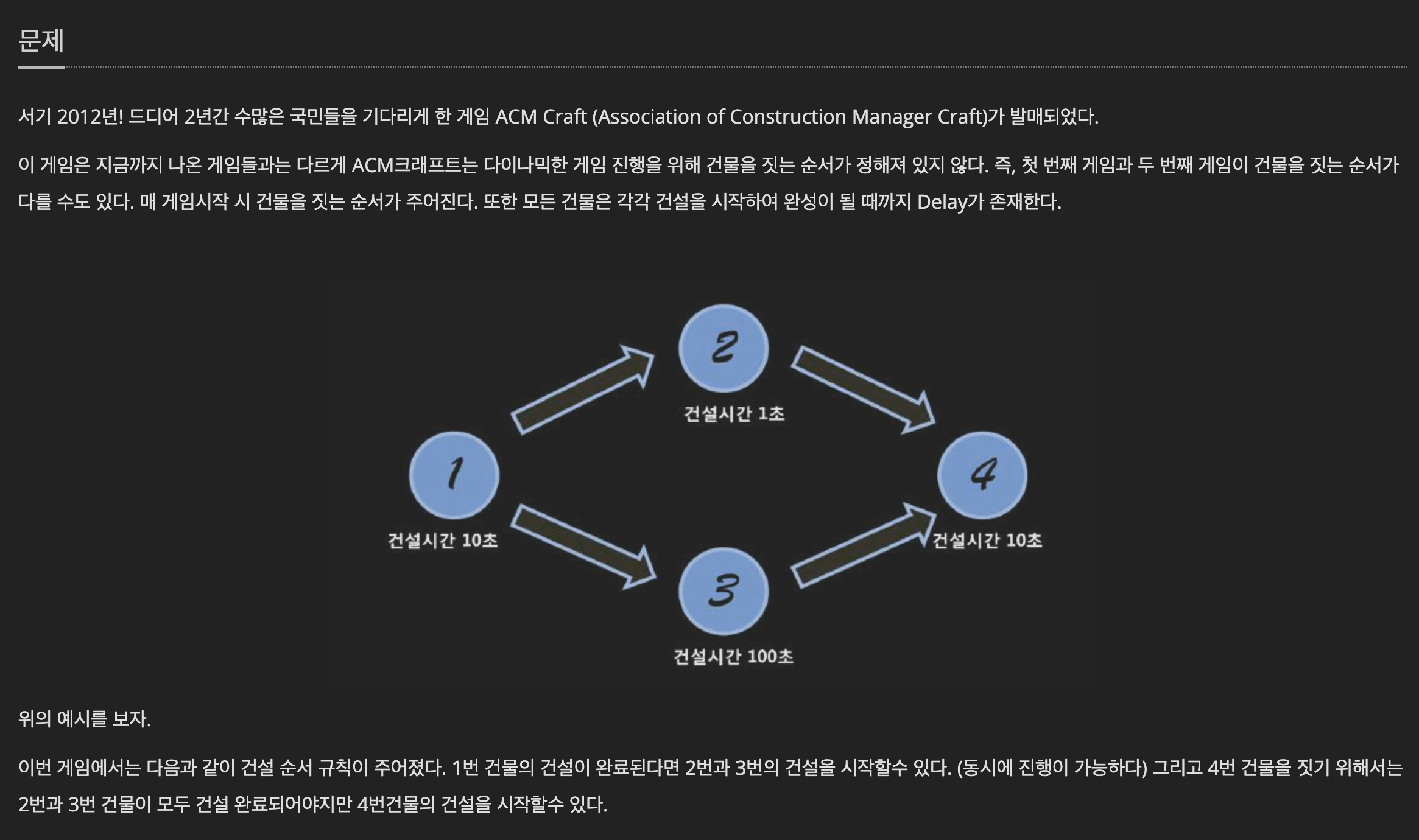
예를 들어 사진 속 4번 건물을 짓기 위해서는 2,3번 건물이 완성되어 있어야 하고, 이를 위해서는 1번 건물이 완성되어 있어야 한다.

1번 건물은 건설 시간이 10초가 걸리고 2번 건물은 1초, 3번 건물은 100초가 걸린다.

2번 건물은 매우 빠르게 완성되지만 결과적으로 4번 건물을 짓기 위해서는 3번 건물이 완성되어야 하기 때문에 총 120초가 걸린다.

나는 이 과정을 아래처럼 정리했다.

4번 건물을 짓기 위해 필요한 과정

1. 4번 건물을 짓기 위해서는 2, 3번 건물이 완성되어야 한다.
2. 2번 건물을 짓기 위해서는 1번 건물이 완성되어야 한다.
3. 3번 건물을 짓기 위해서는 1번 건물이 완성되어야 한다.
4. 이를 루트로 나타내면 1->2->4, 1->3->4 가 된다.
5. 4번 건물을 짓기 전 단계인 2,3번 건물까지 걸리는 건설 시간을 측정하고 그 시간 중 가장 오래 걸리는 시간에 4번 건물 건설 시간을 더해주면 정답이 된다.

위 풀이 과정을 구현하기 위해서는 BFS가 아닌 DP를 사용해야 한다.
DP를 통해 각 건물의 건설까지 걸리는 시간의 최댓값을 저장해주면 될 것이다.

이제 해결해야 할 문제는 단 하나가 남았다.
각 건물의 건설까지 걸리는 시간의 최댓값을 DP로 저장하는건 알겠는데 탐색은 어떻게 할까? 각 건물을 건설하기 위해서는 이전에 건설되어야 할 건물이 거미줄처럼 엮여 있다.
나는 이를 해결하지 못했고, 조언을 구해 위상정렬이라는 키워드를 얻을 수 있었다.

위상정렬 정리

풀이 코드

import sys
input = lambda: sys.stdin.readline().rstrip()
from collections import deque

T = int(input())

for _ in range(T):
    N, K = map(int, input().split()) # 건물 갯수, 건물 건설 규칙 수
    t = [0] + list(map(int,input().split()))
    graph = [[] for _ in range(N+1)]
    indegree = [0] * (N + 1) # 진입 차수 계산
    for _ in range(K):
        x,y = map(int, input().split())
        graph[x].append(y)
        indegree[y] += 1

    dp = [0]*(N+1)
    q = deque()
    # 위상 정렬
    for i in range(1,N+1):
        if indegree[i] == 0:
            q.append(i)
            dp[i] = t[i]
    
    while q:
        n = q.popleft()

        for v in graph[n]:
            dp[v] = max(dp[v], dp[n]+t[v])
            indegree[v] -= 1
            if indegree[v] == 0:
                q.append(v)
    print(dp[int(input())])