다익스트라(Dijkstra) 알고리즘
-
가중치 그래프 상에서 출발노드에서 목표노드까지 이동하는 가장 최단 경로를 찾는다.
-
하나의 출발 노드에서 다른 모든 노드로의 최단 경로를 구할 수 있다.
-
간선은 모두 양수여야 한다.
-
인접 행렬로 표현된 그래프의 경우 시간 복잡도는 O(n^2)이다.
-
우선순위 큐 사용하여 시간 복잡도 O(mlog n)까지 낮출 수 있다. → 개선된 다익스트라 알고리즘
-
그리디 알고리즘과 동적 계획법 사용한다.
다익스트라 알고리즘 과정
1) 아직 방문하지 않은 정점 중 출발지로부터 가장 가까운 정점 방문한다.
2) 해당 정점을 거쳐 갈 수 있는 정점의 거리가 이전 기록한 값보다 적으면 갱신한다.
ex) pq는 우선순위 큐로 정점과 출발지에서 정점까지 가는 최소 거리를 저장한다. 우선순위는 거리가 짧을수록 높다.
구현 예시
(1) pq는 우선순위 큐로 정점과 출발지에서 정점까지 가는 최소 거리를 저장한다. 우선순위는 거리가 짧을수록 높다.
check는 boolean 배열로 해당 정점을 방문하는지 체크한다.
dist는 int 배열로 출발지에서 최소 거리를 기록한다.

(2) 출발지 4를 우선순위 큐에 넣는다. 출발지이므로 거리는 0이다.

(3) 우선순위 큐에서 하나 꺼내 nowVertex에 저장하고 방문체크를 한다. nowVertex을 거쳐 갈 수 있는 정점의 거리가 이전 기록한 값보다 적으면 갱신한다.
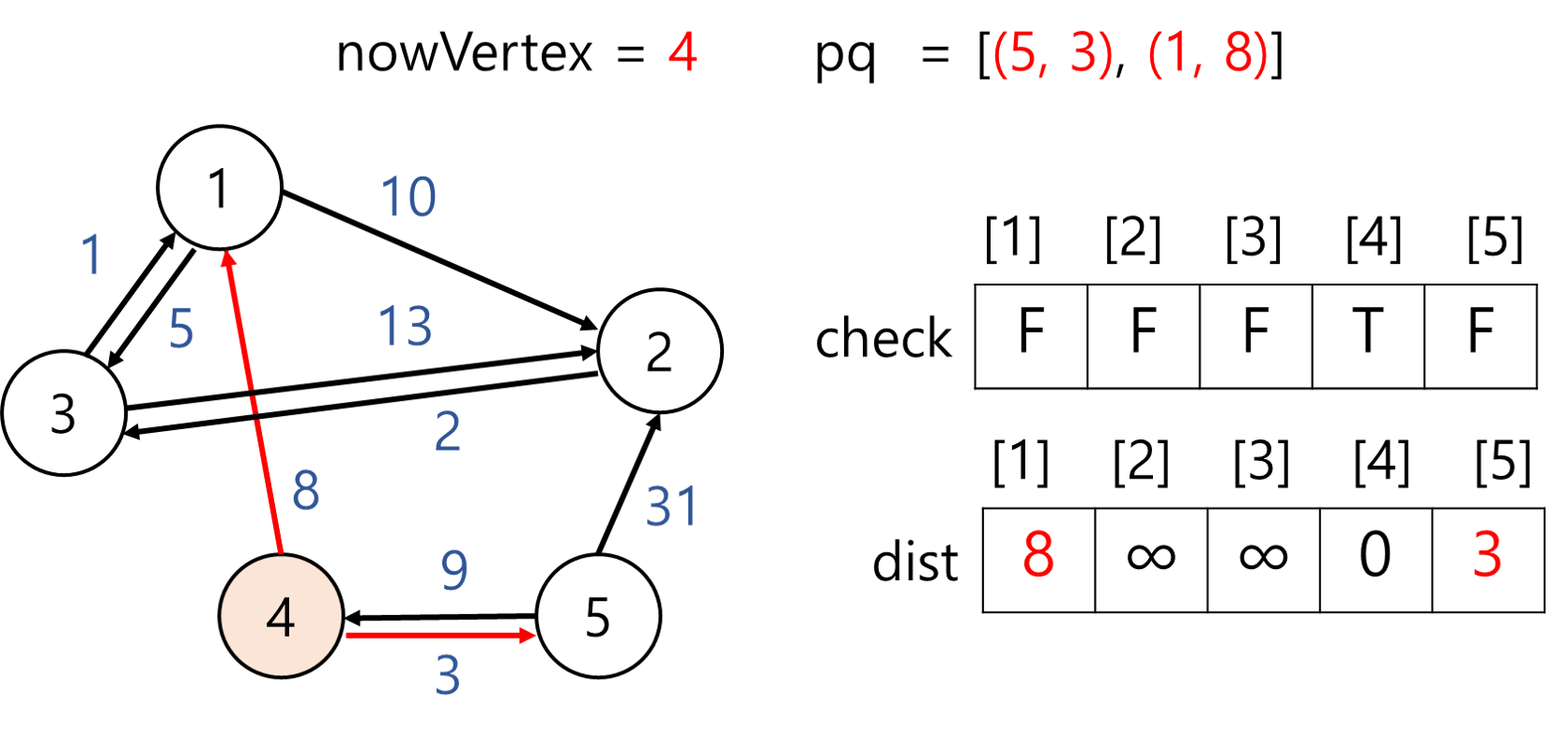
nowVertex는 4이다. 정점 4와 인접한 정점은 1과 5가 있다.
-
dis[1] = 8로 변경
처음 정점은 출발지이기 때문에 1로 가는 거리가 8이므로 dist[1] 값을 8로 갱신한다. 우선순위 큐에 정점 1과 1까지 가는 거리인 8을 추가한다. -
dist[5] = 3로 변경
같은 이유로 변경해준다.
(4) 우선순위 큐에 값이 있으므로 하나 꺼내 nowVertex에 저장하고 방문 처리한다.
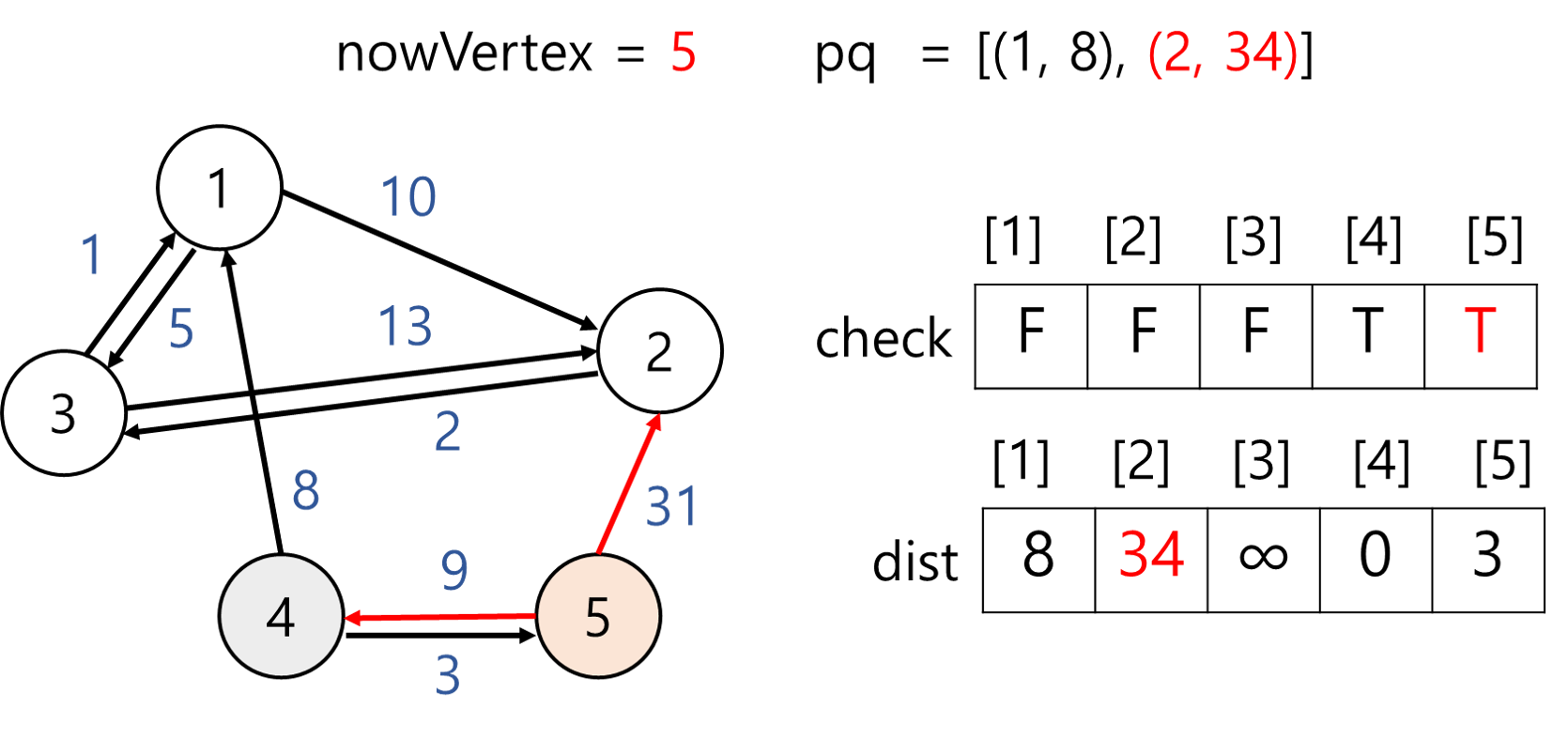
nowVertex = 5이고 방문하지 않았으므로 방문 체크 후 인접 정점 살펴본다. 정점 5과 인접한 정점은 4와 2가 있다.
-
dist[2] = 34로 값 변경
출발지에서 정점 2로 가는 값을 살펴준다. 이 때 경우는 2가지이다.
① 지금까지 계산한 출발지 ~ 정점 2 최단 거리 = dist[2]
② 출발지에서 정점 5를 지나서 정점 2를 가는 거리 = dist[5] + 정점 5에서 정점 2로 가는 거리(=간선의 가중치)
과 ②를 비교하여 더 작은 값을 dist[2]에 기록한다.
①과 ② 를 계산해보자.
① dist[2] = 무한
② dist[5] + 정점 5에서 정점 2로 가는 거리 = 3 + 31 = 34
① > ② 이므로 값을 갱신하고 우선순위 큐에 해당 정점을 추가한다.(2, 34) -
dist[4] 값 변경 x
① dist[4] = 0이다.
② dist[5] + 정점 5에서 정점 4로 가는 거리 = 3+ 9 = 12이다.
① < ② 이므로 값 갱신하지 않는다.
(5) 우선순위 큐에서 값을 꺼낸다.
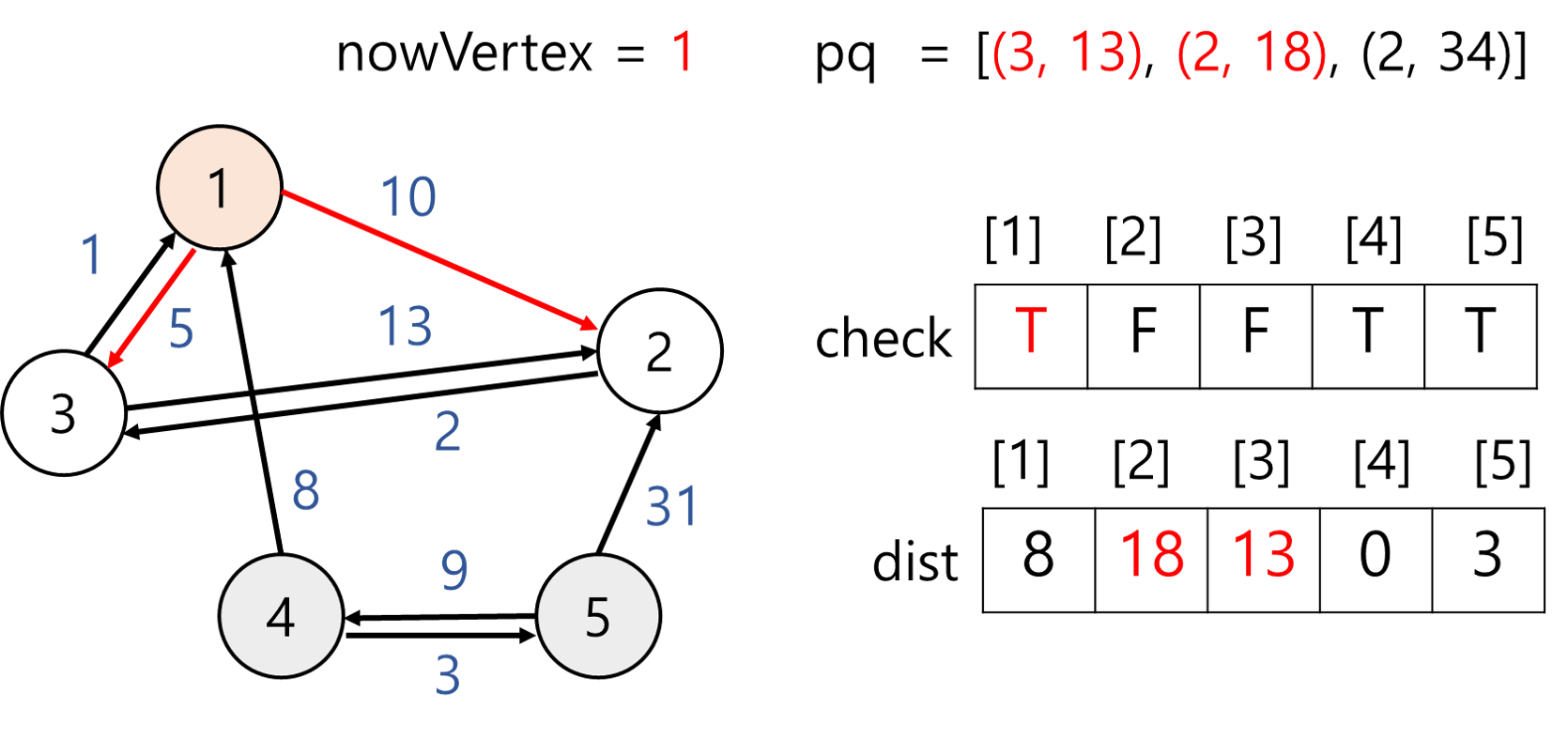
nowVertex = 1이고 방문하지 않았으므로 방문 체크 후 인접 정점 살펴본다. 정점 1과 인접한 정점은 2와 3이 있다.
-
dist[2] = 18로 값 변경
① dist[2] = 34
② dist[1] + 정점 1에서 정점 2로 가는 거리 = 8 + 10 = 18
① > ② 이므로 값을 갱신하고 우선순위 큐에 해당 정점을 추가한다.(2, 18) -
dist[3] = 13로 값 변경
① dist[3] = 무한
② dist[1] + 정점 1에서 정점 3로 가는 거리 = 8 + 5 = 13
① > ② 이므로 값을 갱신하고 우선순위 큐에 해당 정점을 추가한다.(3, 13)
(6) 우선순위 큐에서 값을 꺼낸다.
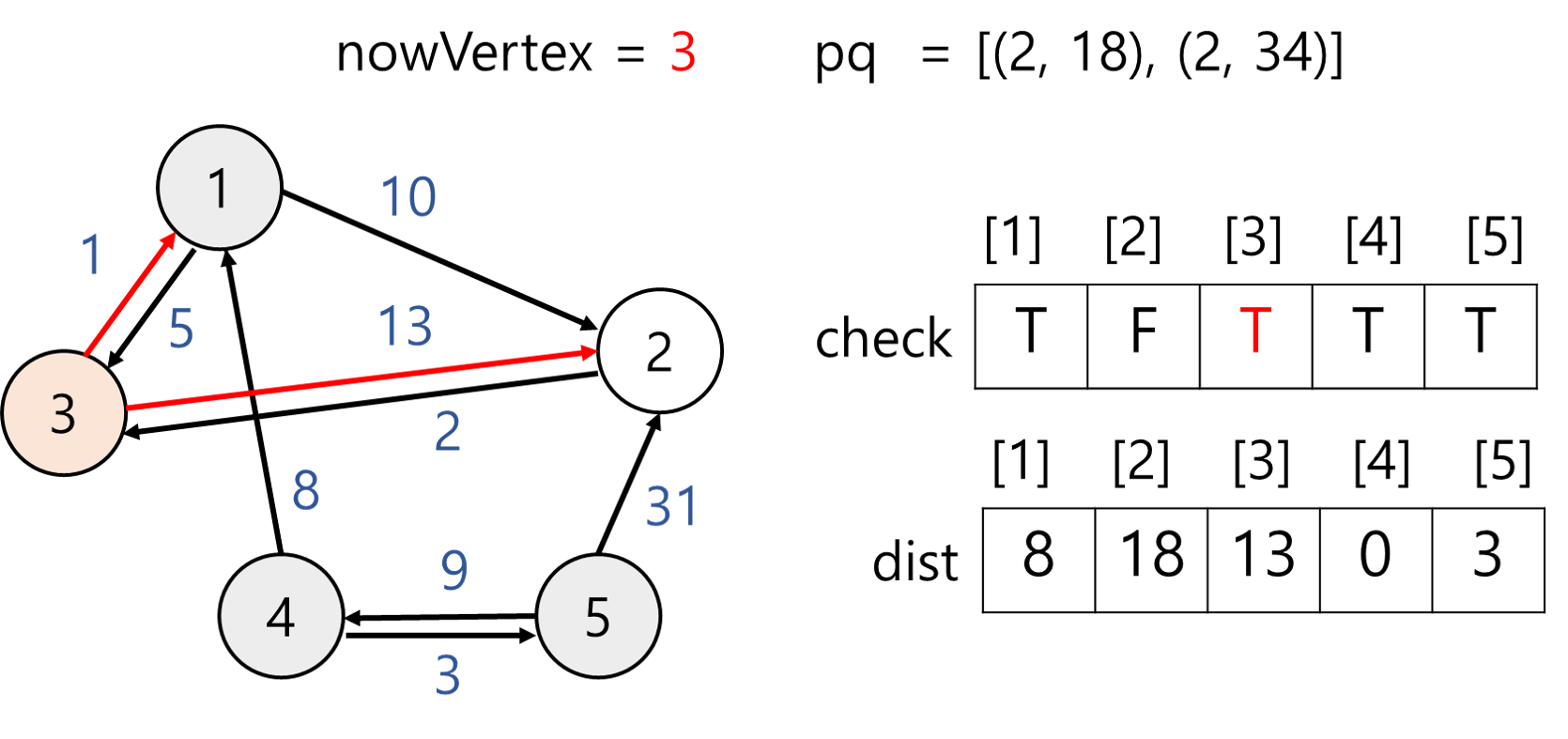
nowVertex = 3이고 방문하지 않았으므로 방문 체크 후 인접 정점 살펴본다. 정점 3과 인접한 정점은 1과 2가 있다.
-
dist[1]값 변경x
① dist[1] = 8
② dist[3] + 정점 3에서 정점 1로 가는 거리 = 13 + 1 = 14
① < ② 이므로 값을 갱신하지 않는다. -
dist[2]값 변경x
① dist[2] = 18
② dist[3] + 정점 3에서 정점 2로 가는 거리 = 13 + 13 = 26
① < ② 이므로 값을 갱신하지 않는다.
(7) 우선순위 큐에서 값을 꺼낸다.
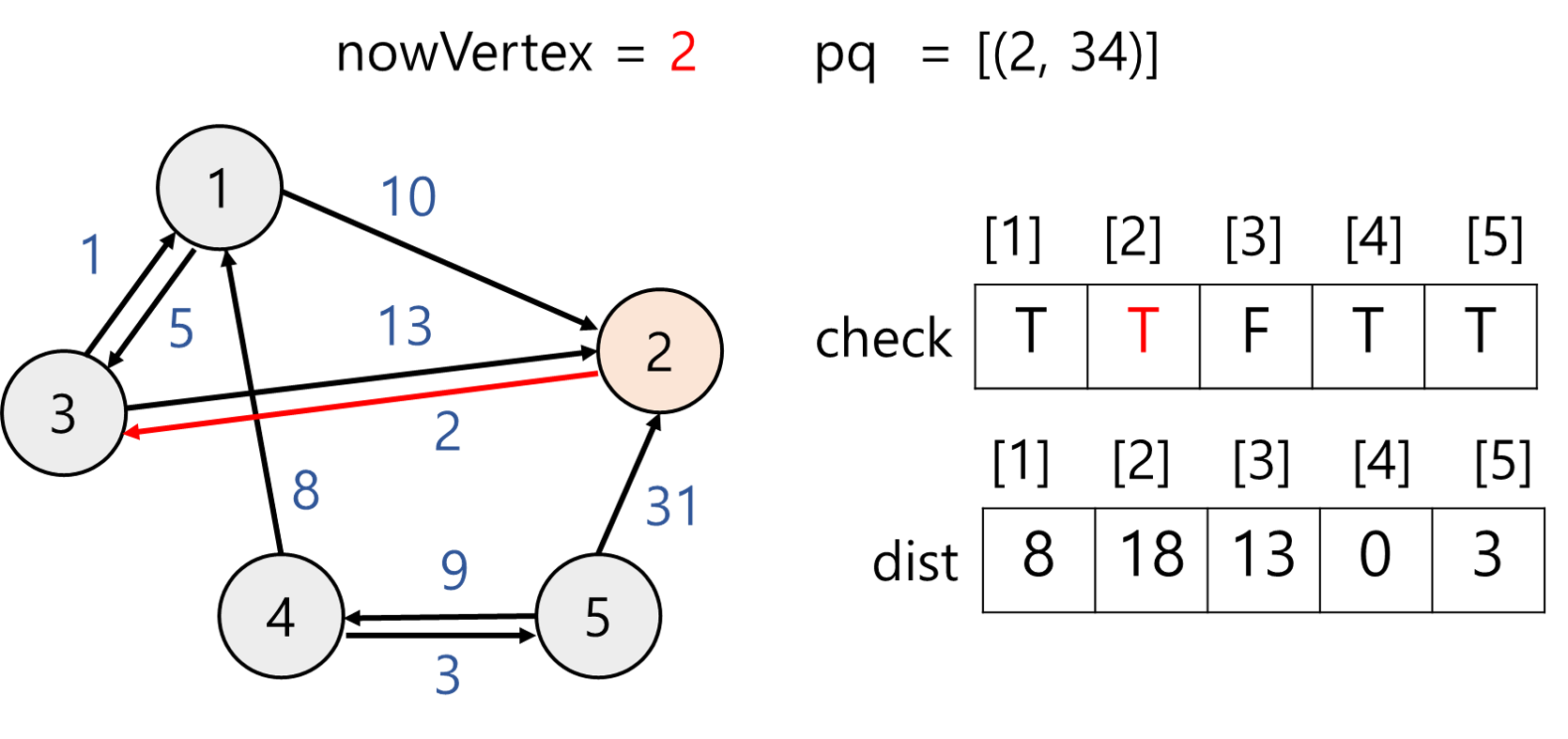
nowVertex = 2이고 방문하지 않았으므로 방문 체크 후 인접 정점 살펴본다. 정점 2과 인접한 정점은 3이다.
- dist[3] 값 변경x
① dist[3] = 13
② dist[2] + 정점 2에서 정점 3로 가는 거리 = 18 + 2 = 20
① < ② 이므로 값을 갱신하지 않는다.
(8) 우선순위 큐에서 값을 꺼낸다.
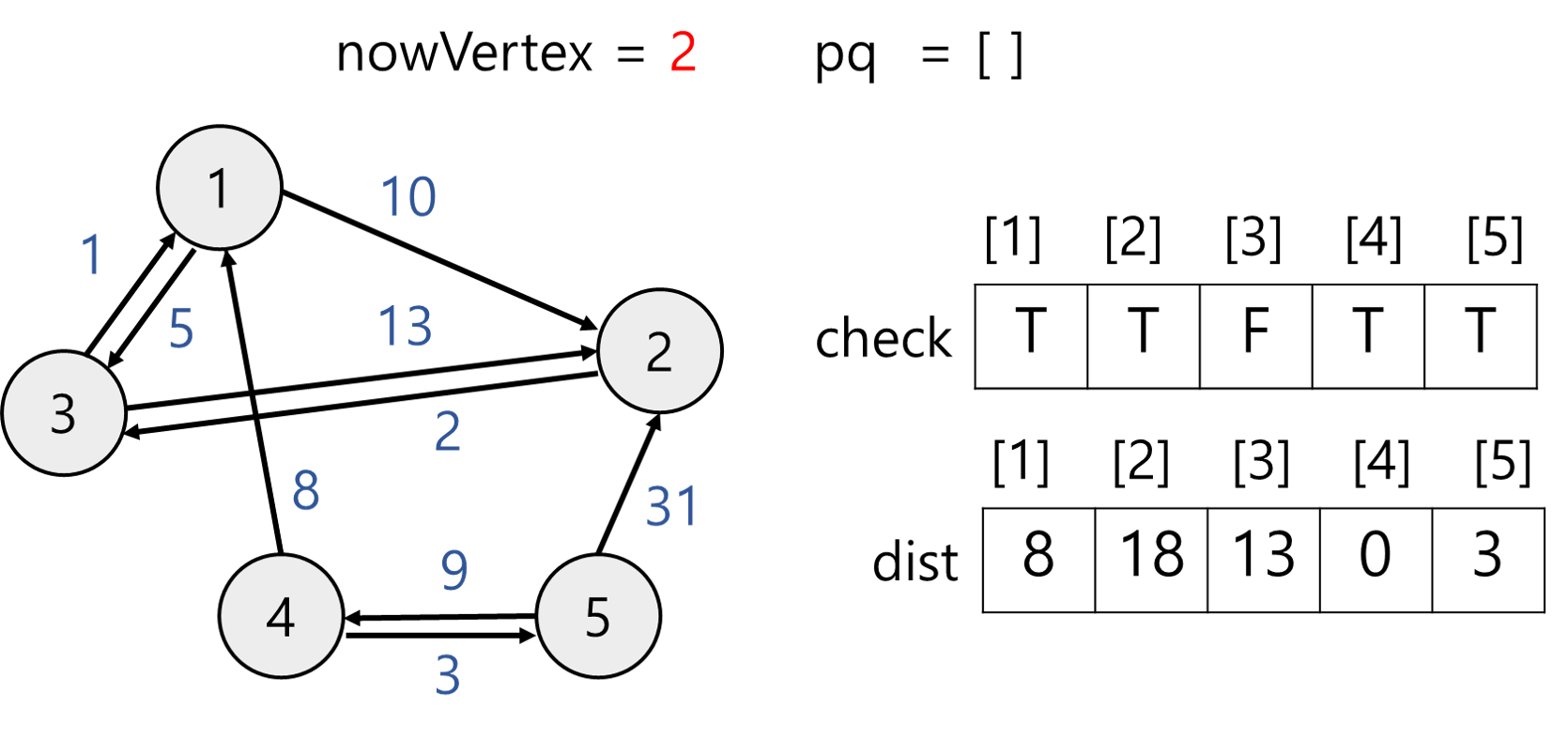
nowVertex = 2이고 방문했으므로 다음으로 넘어간다.
(9) 우선순위 큐에서 값을 꺼낸다.
우선순위 큐가 비었으므로 다익스트라 알고리즘을 종료한다. 정점 4에서 출발하여 다른 정점까지 최소 거리는 다음 dist 배열과 같다.


