[Algorithm] 시간복잡도

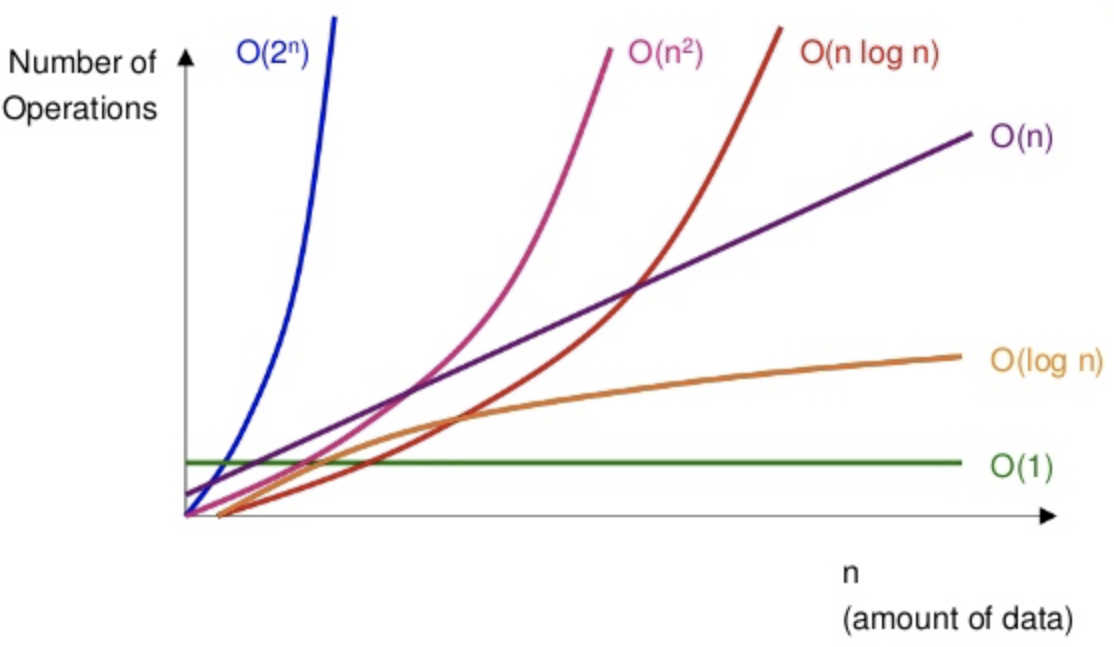
시간복잡도

알고리즘에서 시간복잡도란 주어진 문제를 해결하기 위한 연산 횟수를 말한다. 일반적으로 수행 시간은 1억 번의 연산을 1초의 시간으로 간주하여 예측한다.

시간복잡도의 유형

• 빅-오메가(Ω(n)) : 최선일 때의 연산 횟수를 나타낸 표기법
• 빅-세타(θ(n)) : 보통일 때의 연산 횟수를 나타낸 표기법
• 빅-오(O(n)) : 최악일 때의 연산 횟수를 나타낸 표기법

보통은 빅-오 표기법을 기준으로 수행 시간을 계산하는 것이 좋다.

빅-오 표기법의 시간복잡도

이미지 출처

표기법	이름	시간 복잡도	설명	예시
O(1)	상수	상수 시간	입력 크기와 상관없이 일정한 실행 시간을 가진다	배열에서 원소 하나 찾기
O(logn)	로그	로그 시간	입력 크기가 증가함에 따라 실행시간이 로그함수 형태로 증가한다	이진 탐색 알고리즘
O(n)	선형	선형 시간	입력 크기와 비례하는 실행시간을 가진다	선형 탐색 알고리즘
O(nlogn)	로그선형	선형로그 시간	입력 크기가 증가함에 따라 실행 시간이 로그함수와 선형 함수의 곱의 형태로 증가한다	병합정렬, 힙 정렬 알고리즘
O(n^2)	이차	이차 시간	입력 크기의 제곱에 비례하는 실행시간을 가진다	선택 정렬, 버블 정렬, 퀵 정렬 알고리즘
O(2^n)	지수	지수 시간	입력 크기의 지수에 비례하는 실행시간을 가진다	부분집합
O(n!)	계승	팩토리얼 시간	입력 크기의 팩토리얼에 비례하는 실행시간을 가진다	외판원 문제

예시

• O(1) : 상수 시간 알고리즘
  배열에서 원소 하나 찾기

	public static int find(int[] nums) {
    	return nums[0];
    }

• O(logn) : 로그 시간 알고리즘
  이진 탐색 알고리즘 예시

	public class BinarySearch {
	static int[] arr = {1, 3, 5, 7, 8, 10, 20, 35, 99, 100};

	public static void main(String[] args) {
		System.out.println("1. 순환 호출을 이용한 이진 탐색");
		System.out.println(binarySearch1(5, 0, arr.length-1)); // 2
		
		System.out.println("\n2. 반복을 이용한 이진 탐색");
		System.out.println(binarySearch2(20, 0, arr.length-1)); // 6
		
	}
    // 재귀적 탐색
   static int binarySearch1(int key, int low, int high) {
   	int mid;
    
    if(low<=high) {
    	mid = (low+high)/2;
        
        if(key == arr[mid]) {
        	return mid;
        } else if(key < arr[mid]) {
        	return binarySearch1(key ,low, mid-1); // 왼쪽  탐색 
        } else {
        	return binarySearch1(key, mid+1, high); // 오른쪽  탐색 
        }
    }
    return -1;
   }
   
   // 반복적 탐색
	static int binarySearch2(int key, int low, int high) {
		int mid;
		
		while(low <= high) {
			mid = (low + high) / 2;
			
			if(key == arr[mid]) {
				return mid;
			} else if(key < arr[mid]) {
				high = mid - 1;
			} else {
				low = mid + 1;
			}
		}
		
		return -1; // 탐색 실패 
	}

• O(n) : 선형 시간 알고리즘
  선형 탐색 알고리즘 예시

	public static int LinearSearch(int[] arr, int find) {
    for (int i = 0; i < arr.length; i++) {
        // 찾는 값이 배열에 있으면
        // 그것의 위치를 반환함.
        if (find == arr[i]) {
          return i;
        }
    }

    // 찾는 값이 없음.
    return -1;
}

• O(nlogn) : 선형 로그 시간 알고리즘
  병합 정렬 알고리즘 예시

	public class MergeSort {
    public void sort(int[] arr, int left, int right) {
        if (left == right) {
            return;
        }

        // 중간 인덱스
        int mid = (left + right) / 2;

        // 왼쪽 정렬
        sort(arr, left, mid);
        // 오른쪽 정렬
        sort(arr, mid + 1, right);

        // 배열 합치기
        merge(arr, left, mid, right);
    }

    public void merge(int[] arr, int left, int mid, int right) {
        int n1 = mid - left + 1; // 왼쪽 배열의 길이
        int n2 = right - mid; // 오른쪽 배열의 길이

        // 왼쪽 배열 오른쪽 배열
        int[] leftTemp = new int[n1];
        int[] rightTemp = new int[n2];

        // 왼쪽 배열 담기
        for (int i = 0; i < n1; i++) {
            leftTemp[i] = arr[left + i];
        }
        // 오른쪽 배열 담기
        for (int i = 0; i < n2; i++) {
            rightTemp[i] = arr[mid + 1 + i];
        }

        // 왼쪽 배열과 오른쪽 배열의 인덱스
        int i = 0, j = 0;
        // 원본 배열 arr의 시작 인덱스
        int k = left;

        // 원본 배열에 정렬
        while (i < n1 && j < n2) {
            if (leftTemp[i] <= rightTemp[j]) {
                arr[k] = leftTemp[i];
                i++;
            } else {
                arr[k] = rightTemp[j];
                j++;
            }
            k++;
        }

        // 남아 있는 요소 담기
        while (i < n1) {
            arr[k] = leftTemp[i];
            i++;
            k++;
        }

        while (j < n2) {
            arr[k] = rightTemp[j];
            j++;
            k++;
        }
    }
    
    public class Main {
    public static void main(String[] args) {
        int[] array = {38, 27, 43, 3, 9, 82, 10};
        MergeSort mergeSort = new MergeSort();
        
        mergeSort.sort(array, 0, array.length - 1);

        for (int i : array) {
            System.out.print(i + " ");
        }
    }
}

}

• O(n^2) : 이차 시간 알고리즘
  선택 정렬 알고리즘 예시

import java.util.Arrays;

public class SelectionSort {
	static int[] nums;

	public static void main(String[] args) {
		nums = new int[10];
		for (int i = 0; i < 10; i++) {
			nums[i] = (int) (Math.random() * 10);
		}
		System.out.println("<정렬 전>");
		System.out.println(Arrays.toString(nums));
		
		for(int i = 0; i < nums.length - 1; i++) {
			// 현재 탐색에서 가장 앞의 원소를 초기 값으로 설정해둔다.
			int MinIndex = i;
			// 탐색을 진행하며, 가장 작은 값을 찾는다.
			for(int j = i + 1; j < nums.length; j++) {
				if(nums[MinIndex] > nums[j])
					MinIndex = j;
			}
			// 탐색이 완료되면 가장 작은 값을 가장 앞의 원소와 가장 작은 원소의 위치를 바꾸어준다.
			int temp = nums[MinIndex];
			nums[MinIndex] = nums[i];
			nums[i] = temp;
		}
		
		System.out.println("<정렬 후>");
		System.out.println(Arrays.toString(nums));
	}
}

• O(2^n) : 지수 시간 알고리즘
  부분집합 알고리즘 예시

	public class PowerSet {
    public static void main(String[] args) {
        int[] arr = {1, 2, 3};
        int n = 3;
        boolean[] visited = new boolean[n];

        powerSet(arr, visited, n, 0);
        bit(arr, n);
    }

    static void powerSet(int[] arr, boolean[] visited, int n, int idx) {
        if (idx == n) {
            print(arr, visited, n);
            return;
        }

        visited[idx] = false;
        powerSet(arr, visited, n, idx + 1);

        visited[idx] = true;
        powerSet(arr, visited, n, idx + 1);
    }

    static void bit(int[] arr, int n) {
        for (int i = 0; i < 1 << n; i++) {
            for (int j = 0; j < n; j++) {
                if ((i & 1 << j) != 0)
                    System.out.print(arr[j] + " ");
            }
            System.out.println();
        }
    }

    static void print(int[] arr, boolean[] visited, int n) {
        for (int i = 0; i < n; i++) {
            if (visited[i] == true)
                System.out.print(arr[i] + " ");
        }
        System.out.println();
    }
}

• O(n!) : 팩토리얼 시간 알고리즘

	public void generatePermutations(int[] arr, int n) {
    if (n == arr.length) {
        System.out.println(Arrays.toString(arr));
        return;
    }

    for (int i = n; i < arr.length; i++) {
        swap(arr, i, n);
        generatePermutations(arr, n + 1);
        swap(arr, i, n);
    }
}

private void swap(int[] arr, int i, int j) {
    int temp = arr[i];
    arr[i] = arr[j];
    arr[j] = temp;
}

시간 복잡도 도출 기준

• 상수는 시간 복잡도 계산에서 제외
• 가장 많이 중첩된 반복문의 수행 횟수가 시간 복잡도의 기준

참고 자료 참고 자료2

참고 도서 Do it! 알고리즘 코딩테스트 자바 편