[Algorithm] 이진탐색 (Binary Search)

🔎 이진 탐색

이진탐색은 이분탐색, Binary Search 라고도 한다. 순차적 탐색보다 빠르게 탐색하기 위해 나온 방법이다.

순차적 탐색

• 정렬된 배열 안에서 특정 원소를 찾기 위해서 인덱스 0부터 차례대로 탐색하는 방법이다.

• 원소를 건너뛰는 일 없이 순차적으로 탐색한다.

이진탐색

• 정렬된 배열 안에서 특정 원소를 찾기위해서 인덱스 i부터 j의 중간값과 비교한다.

• 중간값이 찾는 원소가 아니라면 인덱스 i와 j를 다시 정해준다.

• 인덱스 i와 j를 정할 때마다 탐색 범위가 반으로 줄어든다.

ex)

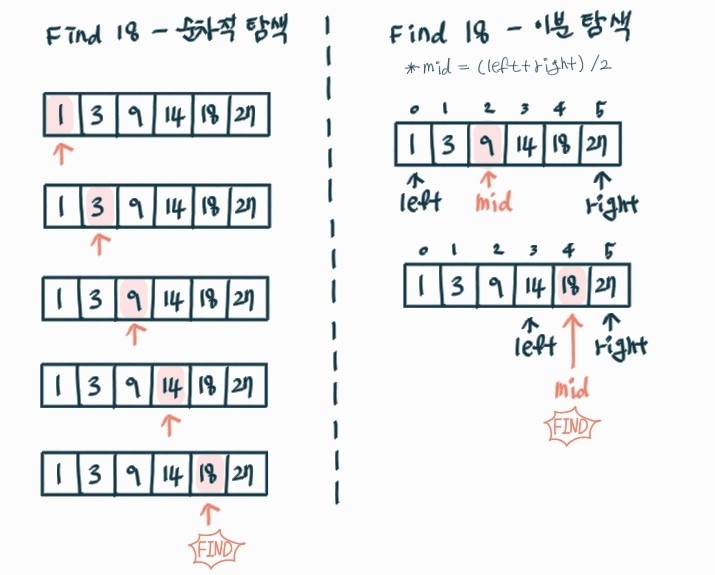
🔎 이진 탐색 방법

1. 처음 범위는 인덱스 0부터 끝까지로 설정하고 탐색한다. 이때 중간 인덱스를 mid라고 한다.

2. mid의 값과 찾는 원소를 비교한다.
   2-1) 찾는 값과 mid의 값이 같다면 탐색 종료한다.

   2-2) mid의 값 < 찾는 값 이라면 left = mid + 1로 설정하고 다시 2를 진행한다.

   2-3) mid의 값 > 찾는 값 이라면 right = mid - 1로 설정하고 다시 2를 진행한다.

3. 만약 left > right가 된다면 찾는 원소가 배열에 없다는 의미이다.

ex 2-2)

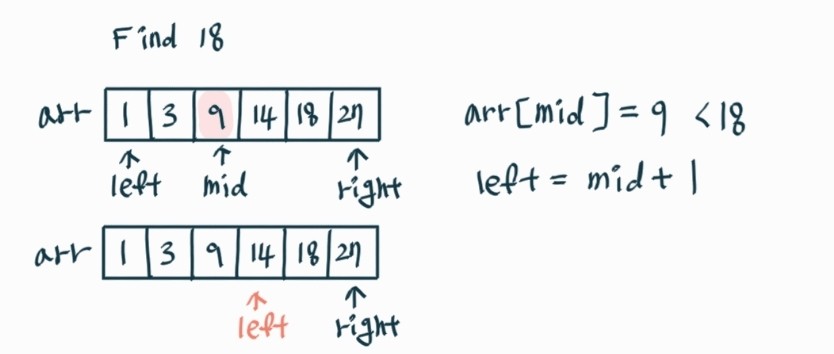
ex 2-3)

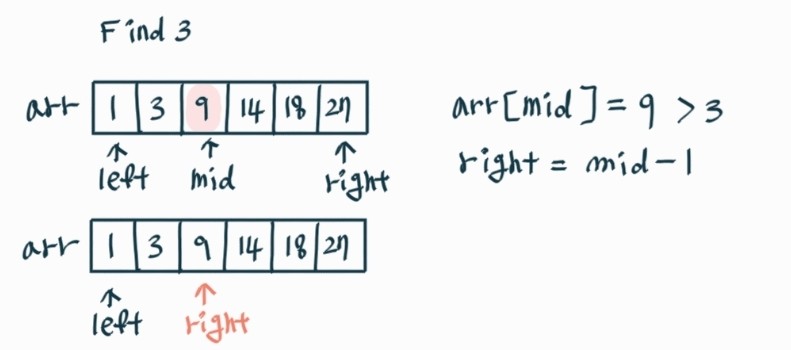
ex 3)

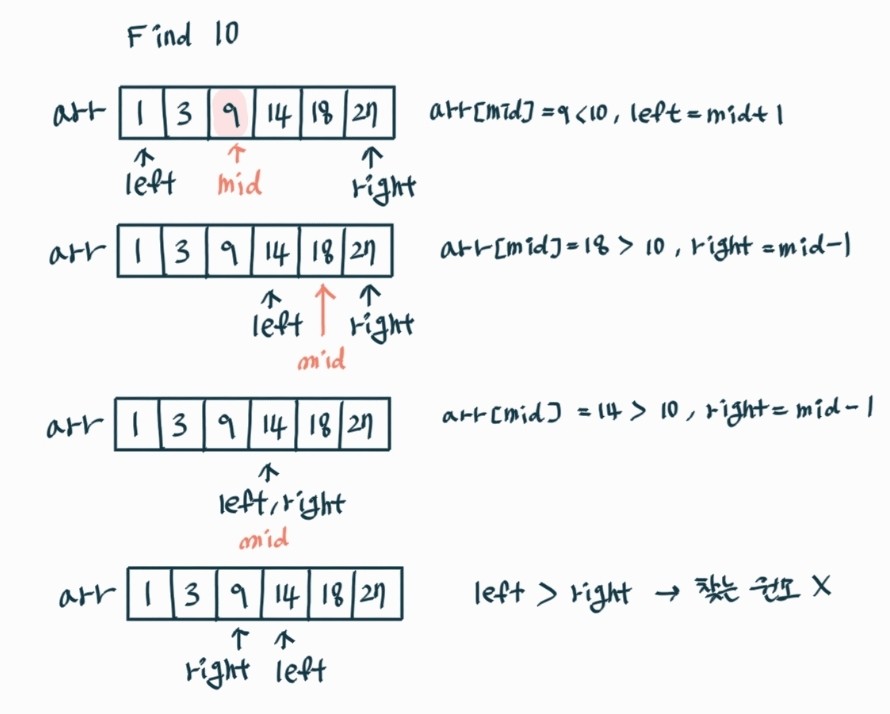
💻 이진 탐색 구현

반복문으로 구현

	public static boolean Binary Search(int[] arr, int n) {
    	int left = 0;
        int right = arr.length - 1;
        int mid;
        
        while(left <= right) {
        	mid = (left + right) / 2;
            if(arr[mid] < n) left = mid + 1;
            else if(arr[mid] > n) right = mid - 1;
            else return true;
        }
        return false;
    }

재귀함수로 구현

	public static boolean BSearchRecursive(int[] arr, int n, int left, int right) {
		if(left > right) return false;
		
		int mid = (left + right) / 2;
        
		if (arr[mid] < n) 
        	return BSearchRecursive(arr, n, mid +1, right);
		else if (arr[mid] > n) 
        	return BSearchRecursive(arr, n, left, mid - 1);
		else 
        	return true;
		
	}

⏰ 시간복잡도

• 순차탐색의 시간복잡도는 O(n)이지만 이진탐색의 시간복잡도는 O(logn)으로 이진탐색이 더 효율적인 것을 볼 수 있다.

참고 do it! 알고리즘 코딩테스트
참고 블로그