소개

PyTorch 프레임워크를 사용하면서 모델의 가중치를 고정하면서도, 기존에 사용하던 방법들(requires_grad, no_grad(), detach() 등)의 차이와 언제 무엇을 사용해야하는지 몰랐습니다.

그래서 requires_grad, no_grad(), detach() 등 여러 방법에 대해 정리하는 글을 작성하던 중 모두 가중치를 고정할 수 있다는 것은 알지만 그 이유에 대해서는 알지 못하였습니다.

결국 'PyTorch의 순전파, 역전파 과정을 정확히 이해해야겠구나'라는 생각이 들어 이 글을 먼저 작성하게 되었습니다.

PyTorch에서 Gradient 계산을 하는 AutoGrad란 무엇이고 어떤 시스템을 따르는가?를 이해 하고자 합니다.

작동 방식만 알고자 하시는 분은 [PyTorch] AutoGrad란 무엇인가? (2)로 넘어 가시면 됩니다.

AutoGrad

PyTorch를 사용하거나 관련 자료를 찾다보면 AutoGrad를 한번 쯤은 들어보셨을 겁니다.

Auto... Grad... 자동 미분? 뭐 그래디언트 계산해주는 거겠지, 자세히는 몰라도 돼~

저는 위처럼 생각했지만 모델의 구조가 복잡해지고 Gradient가 어떻게 흘러갈지 이해해야 하게 돼서 이제는 알아야 한다고 느껴집니다.

그럼 AutoGrad란 무엇일까?

torch.autograd is PyTorch’s automatic differentiation engine that powers neural network training... [중략] Conceptually, autograd keeps a record of data (tensors) & all executed operations (along with the resulting new tensors) in a directed acyclic graph (DAG) consisting of Function objects. - A Gentle Introduction to torch.autograd: pytorch.org

간단하게 설명하면 Directed Acyclic Graph(DAG)의 특성을 가진 연산을 진행하며 그 과정에서 발생하는 연산방법, 데이터 등에 대해 기록하고 Automatic Differentiation을 수행하여 학습이 가능하게 하는 것입니다.

그렇다면 Directed Acyclic Graph는 뭐고 Automatic Differentiation은 무엇일까?

Directed Acyclic Graph (DAG)

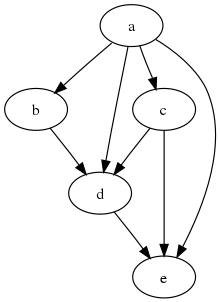
In mathematics, particularly graph theory, and computer science, a directed acyclic graph (DAG) is a directed graph with no directed cycles. That is, it consists of vertices and edges (also called arcs), with each edge directed from one vertex to another, such that following those directions will never form a closed loop. - Directed acyclic graph: WIKIPEDIA

간단하게 말해서 정점(Vertex)과 간선(Edge)를 가진 그래프의 일종이라고 보면 됩니다.

Directed Acyclic Graph는 다음의 특성을 가집니다.

• 일방향성 특징 : 간선 $e_1$로 연결된 두 정점 $v_1,v_2$는 $v_1 \rightarrow v_2$로만 향하거나 $v_2 \rightarrow v_1$로만 향할 수 있다.

• 비순환적 특징 : 특정 정점 $v$에서 시작하여 다시 정점 $v$로 돌아올 수 없다.

PyTorch의 AutoGrad는 연산 중 그래프를 만들게 될 때 DAG의 특징을 따르기 때문에 역전파 과정에서 이전 정점(파라미터)에 빠짐없이 Gradient를 전파할 수 있게됩니다.

Automatic Differentiation (AD)

Automatic Differentiation : In mathematics and computer algebra, automatic differentiation (auto-differentiation, autodiff, or AD), also called algorithmic differentiation, computational differentiation, is a set of techniques to evaluate the partial derivative of a function specified by a computer program. - Automatic differentiation: WIKIPEDIA

Automatic Differentiation은 각 변수의 편미분 값을 구하기 위한 기술의 집합으로 주로 두가지로 나뉩니다.

• Forward Accumulation : 입력 $x$로부터 시작해서 목표 변수로의 기울기를 알아낼 때 까지 기울기를 축적해 나아가는 방식. $\frac{\partial{w_i}}{\partial{x}}=\frac{\partial{w_i}}{w_{i-1}} \cdot \frac{w_{i-1}}{\partial{x}}$

• Reverse Accumulation : 출력 $y$로부터 시작해서 목표 변수로의 기울기를 알아낼 때 까지 기울기를 역으로 축적해 나아가는 방식 $\frac{\partial{y}}{\partial{w_i}}=\frac{\partial{y}}{w_{i+1}} \cdot \frac{w_{i+1}}{\partial{w_i}}$

파이토치의 공식 논문을 살펴본다면 이 중 Reverse Accumulation을 사용한다고 나와있습니다.

그렇다면 이 Forward/Reverse Accumulation이 무엇이고 왜 Reverse Accumulation을 사용하는지에 대해 설명드리겠습니다.

두 방식에 대해 차이점에 대해 이해하기 위해 다음의 예시를 들겠습니다.

Foward Accumultation

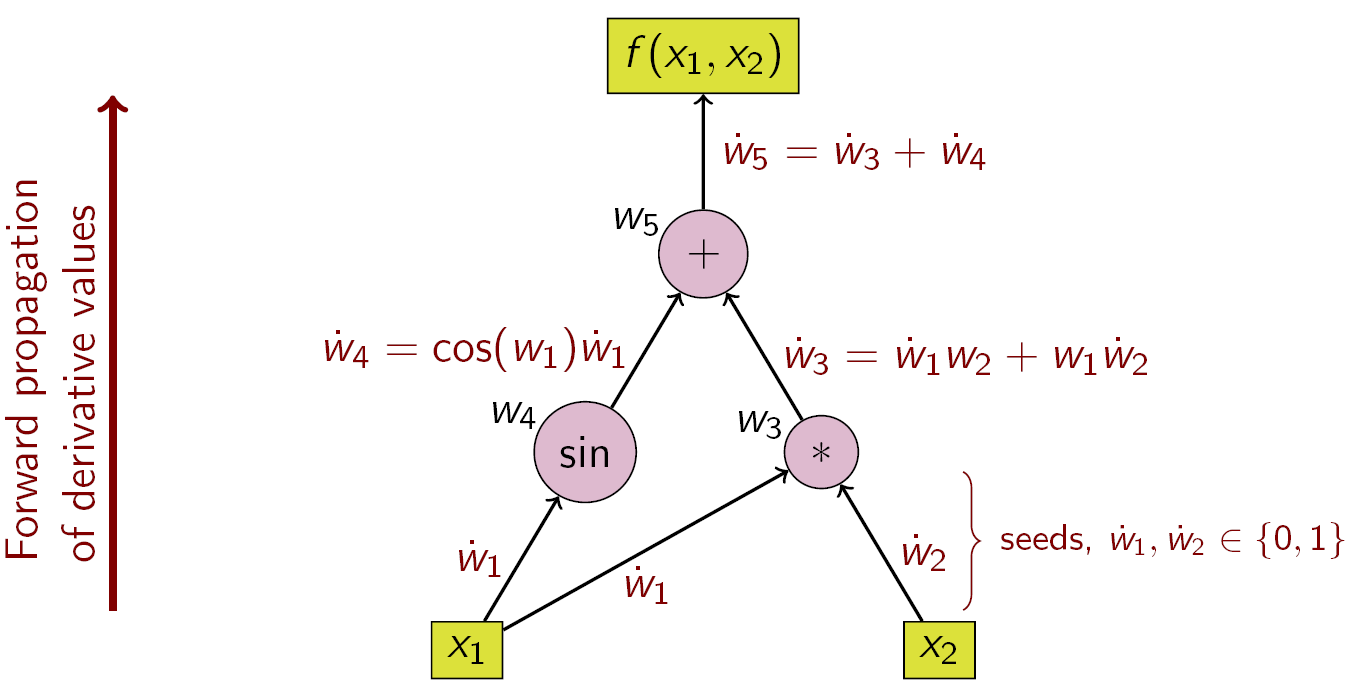
먼저 미분을 수행할 독립변수를 고정하고 각 하위 표현식의 도함수를 재귀적으로 계산합니다.

독립 변수 $x,y$ 중에서 $\frac{\partial{f}}{\partial{x}}=\frac{\partial{w_5}}{\partial{w_1}}$를 구하는 경우를 예시로 들어 다음과 같이 설명해보겠습니다.

1. 우선 $\frac{\partial{w_1}}{\partial{w_1}}=1,\frac{\partial{w_2}}{\partial{w_2}}=0$로 초기화 하겠습니다.

2. $w_3$과 $w_4$를 각각 독립변수들에 대해 미분을 하게 되면 다음과 같습니다.

   • $w_3'=w_1'w_2 + w_1w_2'$ : 곱함수의 미분법

   • $w_4'=cos(w_1)w_1'$ : 삼각함수 미분법

3. 이 때 $w_1' = \frac{\partial{w_1}}{\partial{w_1}}=1$ 이고 $w_2'=\frac{\partial{w_2}}{\partial{w_2}}=0$이므로 $w_3'=w_2$, $w_4'=cos(w_1)$입니다.

4. $w_5$를 각 독립변수들에 대해 미분하게 되면 다음과 같습니다.

   • $w_5'= w_3' + w_4'$ : 일반적인 미분법

5. 이때 $w_3'=w_2$, $w_4'=cos(w_1)$ 이므로 $w_5'= w_2+ cos(w_1)$이 됩니다.

이를 연쇄법칙으로 $\frac{\partial{f}}{\partial{x}}=\frac{\partial{w_5}}{\partial{w_1}}$를 구하는 과정을 보이면 다음과 같습니다.

1. $\frac{\partial{w_1}}{\partial{w_1}}=1$로 고정합니다.

2. $w_1$과 연관된 출력 $w_3,w_4$로 연쇄 법칙을 이어갑니다.

   • $\frac{\partial{w_3}}{\partial{w_1}}\cdot \frac{\partial{w_1}}{\partial{w_1}}= w_2 \cdot 1$

   • $\frac{\partial{w_4}}{\partial{w_1}}\cdot \frac{\partial{w_1}}{\partial{w_1}}= cos(w_1) \cdot 1$

3. $w_3,w_4$ 모두 출력 $w_5$와 연관되어 있으므로 연쇄법칙을 이어갑니다.

   • $\frac{\partial{w_5}}{\partial{w_3}}\cdot\frac{\partial{w_3}}{\partial{w_1}}\cdot \frac{\partial{w_1}}{\partial{w_1}} = 1 \cdot w_2 \cdot 1$

   • $\frac{\partial{w_5}}{\partial{w_4}}\cdot\frac{\partial{w_4}}{\partial{w_1}}\cdot \frac{\partial{w_1}}{\partial{w_1}} = 1 \cdot cos(w_1) \cdot 1$

4. 이때 $w_5$에 두 경로로 들어오게 되므로 최종적으로 $\frac{\partial{w_5}}{\partial{w_1}}$는 다음과 같이 정의 됩니다.

   • $\frac{\partial{w_5}}{\partial{w_3}}\cdot\frac{\partial{w_3}}{\partial{w_1}}\cdot \frac{\partial{w_1}}{\partial{w_1}}+\frac{\partial{w_5}}{\partial{w_4}}\cdot\frac{\partial{w_4}}{\partial{w_1}}\cdot \frac{\partial{w_1}}{\partial{w_1}}=1 \cdot w_2 \cdot 1 + 1 \cdot cos(w_1) \cdot 1= w_2+cos(w_1)$

위의 예시로 보면서 살펴 보았을 때 Foward Accumulation의 특징은 특정 입력 변수로부터 시작하여 특정 입력에 대한 모든 출력의 변화량을 계산하게 됩니다.

입력 변수의 개수가 많아지게 되면 각 입력 변수에 대해 위와 같은 과정을 한번 씩 진행해야 하므로 연산량이 크게 증가하게 됩니다.

이러한 이유로 Foward Accumulation은 입력이 적은 경우에 자주 쓰이며, 특정 입력에 대한 출력의 변화량이 중요한 경우에 사용됩니다.

Reverse Accumultation

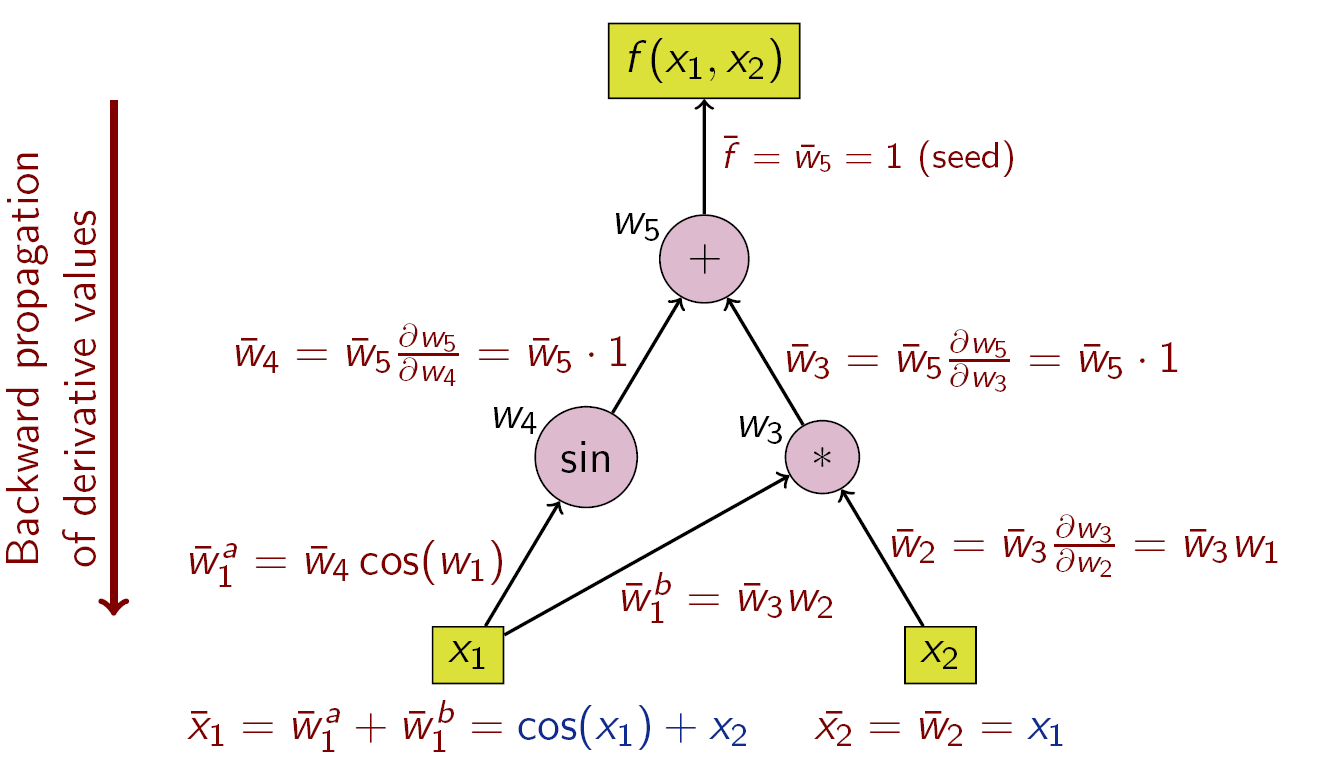
의존 변수는 고정되어 있으며 각 하위 표현식에 대해 재귀적으로 도함수를 계산합니다.

의존 변수 $f(x,y)=w_5$ 에 대해서 $\frac{\partial{f}}{\partial{x}}=\frac{\partial{w_5}}{\partial{w_1}}$를 구하는 경우를 예시로 들어 다음과 같이 설명해보겠습니다.

1. 우선 $\frac{\partial{w_5}}{\partial{w_5}}=1$로 초기화 하겠습니다.

2. $w_5$ 에 연관된 입력 $w_3,w_4$에 대한 변화량을 구하게 되면 다음과 같습니다.

   • $\frac{\partial{w_5}}{\partial{w_3}}=1$

   • $\frac{\partial{w_5}}{\partial{w_4}}=1$

3. $w_3'$에 연관된 입력 $w_1,w_2$에 대한 변화량을 구하게 되면 다음과 같습니다.

   • $\frac{\partial{w_3}}{\partial{w_1}}=w_2$

   • $\frac{\partial{w_3}}{\partial{w_2}}=w_1$

4. 동일하게 $w_4'$에 연관된 입력 $w_1$에 대한 변화량을 구하게 되면 다음과 같습니다.

   • $\frac{\partial{w_4}}{\partial{w_1}}=cos(w_1)$

5. 이때 $w_5$에서 $w_1$으로 들어오는 모든 경로를 연쇄법칙과 함께 표현하면 다음과 같습니다.

   • $\frac{\partial{w_5}}{\partial{w_5}}\cdot\frac{\partial{w_5}}{\partial{w_3}}\cdot \frac{\partial{w_3}}{\partial{w_1}}=1\cdot 1 \cdot w_2$

   • $\frac{\partial{w_5}}{\partial{w_5}}\cdot\frac{\partial{w_5}}{\partial{w_4}}\cdot \frac{\partial{w_4}}{\partial{w_1}}=1\cdot 1 \cdot cos(w_1)$

6. 최종적으로 $\frac{\partial{w_5}}{\partial{w_1}}$을 다음과 같이 표현할 수 있습니다.

   • $\frac{\partial{w_5}}{\partial{w_5}}\cdot\frac{\partial{w_5}}{\partial{w_3}}\cdot \frac{\partial{w_3}}{\partial{w_1}}+\frac{\partial{w_5}}{\partial{w_5}}\cdot\frac{\partial{w_5}}{\partial{w_4}}\cdot \frac{\partial{w_4}}{\partial{w_1}}=1\cdot 1 \cdot w_2+1\cdot 1 \cdot cos(w_1)=w_2+cos(w_1)$

위의 예시로 보면서 살펴 보았을 때 Reverse Accumulation의 특징은 특정 출력 변수로부터 시작하여 모든 입력들에 대한 특정 출력의 변화량을 계산하게 됩니다.

위의 예시에서는 최종 출력이 $w_5$ 하나이지만, 출력이 많아진다면 Foward Accumulation 과정과 동일하게 출력을 하나씩 고정하며 기울기 값을 알아내야 합니다.

그렇기 때문에 이 방식은 출력이 많아지게 된다면 각 출력 변수에 대해 위와 같은 과정을 한번 씩 진행해야 하므로 연산량이 크게 증가하게 됩니다.

이러한 이유로 Reverse Accumulation은 출력이 적은 경우에 자주 쓰이며, 입력에 대한 특정 출력의 변화량이 중요한 경우에 사용되게 됩니다.

이러한 특성때문에 많은 파라미터에 대한 출력의 변화량이 중요한 머신러닝과 딥러닝에서는 Reverse Accumulation이 주로 사용되게 됐으며, PyTorch 또한 이러한 흐름을 따라갑니다.

마무리

이번 글은 'AutoGrad란 무엇이고 어떤 시스템을 따르는가?'에 대해서 설명하였습니다.

AutoGrad의 작동과정을 이해하기 전에 AutoGrad가 어떤 시스템을 따르는지 알고 가는 것이 좋다고 생각하였고 DAG와 AD를 이해하고 설명하였습니다.

DAG 부분까지는 쉽게 이해하였지만, Foward Accumulation과 Reverse Accumulation 사이의 차이를 이해하는데 어려워 고생하였습니다...

잘못 된 부분이 있다면 댓글 남겨주시면 감사드리겠습니다.

다음 글에서는 'AutoGrad의 작동 과정'에 대해서 설명을 드리도록 하겠습니다.

References

1. A Gentle Introduction to torch.autograd - PyTorch.org

2. Automatic differentiation in PyTorch - OpenReview

3. What is tape-based autograd in Pytorch? - Stack Overflow

4. Automatic differentiation - WIKIPEDIA

5. Reverse-mode automatic differentiation: a tutorial - Rufflewind's Scratchpad

6. Directed acyclic graph - WIKIPEDIA