[PyTorch] AutoGrad란 무엇인가? (2)

김태훈·2024년 5월 1일

PyTorch autograd

[PyTorch] AutoGrad란 무엇인가?

목록 보기

2/2

소개

이전 글에서는 AutoGrad가 무엇이고 어떤 시스템을 기반으로 작동하는지에 대해 설명하는 글을 작성하였습니다.

이번 글에서는 AutoGrad가 어떻게 연산과 Gradient에 대한 정보를 기록하는지 그 과정에 대해 설명하겠습니다.

AutoGrad 작동 방식

경사하강법을 진행하기 위해서는 기울기에 대한 정보를 알고 있어야 합니다.

또 기울기를 알기 위해서는 연산에 대한 정보, 입력에 대한 정보를 알고 있어야 합니다.

그렇다면 PyTorch에서는 이런 정보들을 어떻게 저장하는지에 대해 알아보기 위해 간단한 예시를 들어 설명하겠습니다.

Tensor 클래스

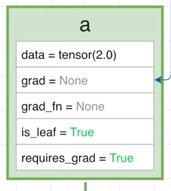
Tensor 클래스는 PyTorch에서 중요한 클래스 중 하나라고 생각합니다.

Tensor 객체 안에는 여러가지 변수들과 메서드들이 담겨 있지만 주요 변수들에 대해 살펴보겠습니다.

data : 실질적인 값이 담겨있습니다.
grad : 역전파된 Gradient에 대한 정보가 담겨있습니다.
grad_fn : 이 Tensor가 생길때 사용된 연산이 어떤 것인지에 대한 정보가 담깁니다.
is_leaf : 현재 텐서가 일반 Tensor인지(True) Tensor 사이의 연산으로 의해 생긴 Tensor인지(False)에 대한 정보입니다.
requires_grad : Gradient 계산을 할 것인지에 대해 정의 됩니다.

Tensor 연산

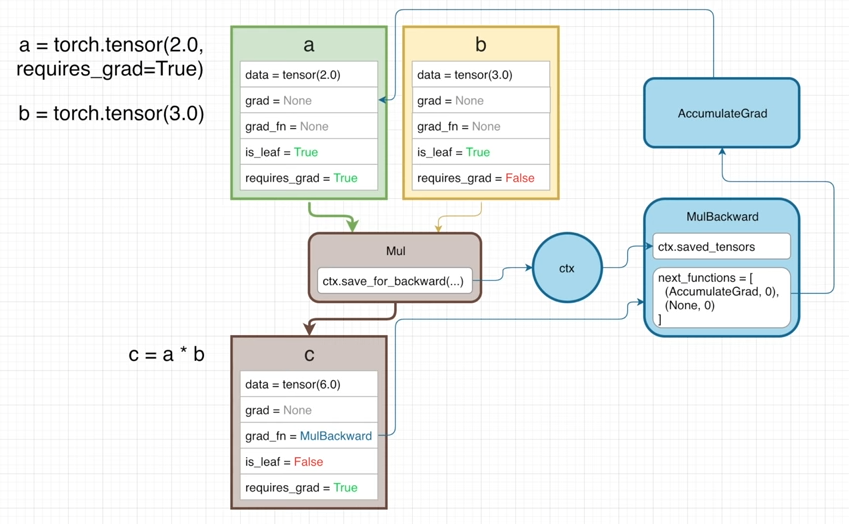
위 예시에서 a*b를 수행하게 될 경우의 과정을 한 번 살펴보겠습니다.

곱하기 과정을 진행할 경우 곱 연산을 담당하게 되는 Mul 연산을 실행하게 됩니다.
Mul 연산에서는 출력 정보를 담을 Tensor c 생성 합니다.

2-1. Mul연산에서는 연산을 진행하면서 결과값을 Tensor c에 기록합니다.

2-2. ctx.save_for_backward() 함수를 실행하여 입력 Tensor들 중 특정 Tensor에 대한 정보를 기록하게 됩니다.

2-3. Tensor c의 grad_fn에 Mul 연산의 Backward 정보인 MulBackward 객체를 선언하여 저장합니다.
생성된 Tensor c는 아래와 같은 특성을 가진 Tensor가 됩니다.

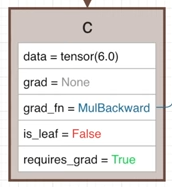
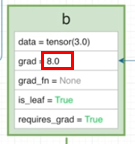
Tensor c

data : a의 데이터와 b의 데이터를 곱한 값
grad : backward 연산을 진행하지 않았기에 값의 변화는 없습니다.
grad_fn : 곱셈과 관련된 grad_fn인 MulBackward가 저장됩니다.
is_leaf : Tensor 사이의 연산으로 생성되었으므로 False가 저장됩니다.
requires_grad : Tensor a의 requires_grad가 True이므로 True가 저장됩니다.

※ 이때 연산에 사용된 Tensor 중 하나라도 requires_grad가 True인 경우 requires_grad가 True가 되게 됩니다.

또한 이렇게 Tensor가 연산에 사용된 경우에 Tensor a, b, c는 각각 연산 그래프에 등록 됐다고 생각하시면 됩니다. (연산 그래프는 DAG로 연산 과정에 대해서 이 글의 썸네일처럼 노드로 표현한 것입니다.)

다음 절에서 이 과정에서 처음 보이는 ctx와 grad_fn은 무엇이고 어떤 역할을 하게되는지 알아보겠습니다.

ctx

Python에서 ctx 자체는 self와 유사한 성격을 가지고 있습니다.

하지만 PyTorch에서 ctx는 @staticmethod 라는 Decorator와 함께 사용되어 메소드 자체가 정적메소드로 정의되기 때문에 ctx는 하나의 인수로 처리됩니다.

이런 ctx가 어떤 정보가 가지고 있고 어떻게 연산에 사용된 Tensor를 다루는지에 대해서 확인해보고자 실제 코드를 찾아보았지만 찾기가 어려웠습니다...

ctx와 관련된 saved_tensor, save_for_backward() 변수, 메서드는 실제로 c언어로 외부에 구현되어 있어 자세히 알 수는 없습니다. (한번 나중에 확인해보겠습니다!)

그렇기 때문에 saved_tensor와 save_for_backward()가 무엇인지만 간단하게 다루겠습니다.

우선 ctx는 간단하게 PyTorch에서 연산에 사용된 변수를 다루는 하나의 객체라고 볼 수 있습니다.

ctx.save_for_backward(self, *tensors: torch.Tensor) : Tensor 연산 단계에서 사용된 변수들에 대해서 역전파 단계에서 필요한 변수들에 대해 저장하는 메소드입니다.
ctx.saved_tensor : 기존에 저장한 변수들에 대한 정보가 담겨있는 변수입니다.

곱셈을 담당하는 MulBackward 객체에서는 이러한 변수들에 대한 정보를 기반으로 Gradient를 계산할 수 있게 됩니다.

가령 곱연산에서는 saved_tensor에 Tensor a, b에 대한 정보가 담겨있을 것이고, 역전파 단계에서 a에게는 Gradient로 b의 값을 b에게는 Gradient로 a의 값을 전달해주면 됩니다.

그렇다면 이렇게 입력 Tensor들의 정보를 기반으로 어떻게 Gradient를 전파하는지에 대해 다음 절에서 확인해보겠습니다.

grad_fn

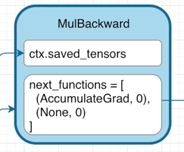
grad_fn은 해당 Tensor 객체가 만들어질 때 사용된 연산과 사용된 Tensor 객체들에 대한 정보가 담긴 하나의 객체가 되고, Backward에서 중요한 역할을 하게 됩니다.

MulBackward 객체에서는 ctx.saved_tensors, next_functions가 있는 것을 확인하실 수 있습니다.

각각의 변수를 설명하면 다음과 같습니다.

ctx.saved_tensors : 연산에 사용된 실질적인 변수들에 대한 정보가 담겨있습니다.
next_functions : 지금까지 축적된 Gradient를 Backward 하게 될 때, 다음에 넘겨줄 Backward 방식에 대한 정보가 담겨있습니다.

그렇다면 위의 예시에서 c의 grad_fn에는 어떤 정보가 담기는지 확인해보겠습니다.

c의 grad_fn에서 next_functions를 보면 list 형식으로 (AccumulationGrad, 0)과 (None, 0)이라는 정보가 담겨있습니다.

왜 list에 두개의 요소가 담겨있는가?

우선 list가 두개의 요소를 가진 이유는 입력이 Tensor a, b로 두개이고, 각 리스트의 요소는 순서대로 입력 순서에 해당하는 각 Tensor에 대한 Backward 연산 정보입니다.

그렇다면 Accumulation은 무엇이고 None은 무엇인가?

Accumulation은 지금까지 축적되어 온 Gradient를 해당 Tensor의 Grad에 저장하라는 의미를 가지며, None은 더이상 Gradient를 축적해 나아갈 필요가 없다는 것입니다.

그럼 왜 Tensor b에는 None이라는 함수가 지정된 것인가?

Tensor b의 requires_grad 변수를 살펴보면 False가 지정되어 있고 이는 Gradient 연산을 하지 않겠다는 의미를 가지고 있습니다.
이 과정은 Tensor 내부의 is_leaf, requires_grad 변수가 중요합니다.

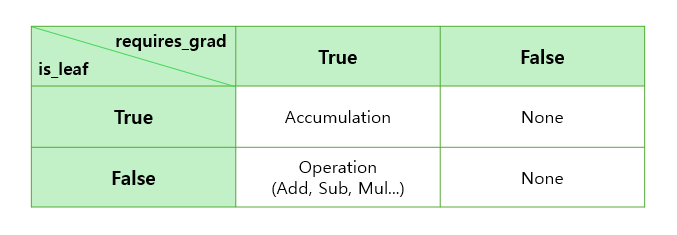
그렇다면 이 MulBackward는 어떻게 작동하는 것인가?에 대해서 다음 절에서 알아보겠습니다.

Operation(Add, Sub, Mul...)

PyTorch에서는 널리 알려진 기본 연산인 사칙연산, 삼각함수, 지수, 로그 등에 대한 함수에 대한 Gradient Function에 대해 미리 정의해놨습니다.

이렇게 미리 정의된 연산에 대한 코드를 살펴보고자 여러 자료를 찾아봤지만 결국 못찾았습니다...

그래서 실제로 따로 grad_fn을 정의할 수 있는 코드를 기반으로 설명하고자 합니다.(내부적 동작은 유사하다고 판단)

어떤 $x$ 에 대한 함수 $P(x)$ 에 대해서 $P(x)=\frac{1}{2}(5x^3-3x), P'(x) = \frac{3}{2}(5x^2-1)$ 로 정의한다고 할 경우 이 함수를 다음과 같이 AutoGrad에 정의할 수 있습니다.

import torch
import math


class LegendrePolynomial3(torch.autograd.Function):
    """
    We can implement our own custom autograd Functions by subclassing
    torch.autograd.Function and implementing the forward and backward passes
    which operate on Tensors.
    """

    @staticmethod
    def forward(ctx, input):
        """
        In the forward pass we receive a Tensor containing the input and return
        a Tensor containing the output. ctx is a context object that can be used
        to stash information for backward computation. You can cache arbitrary
        objects for use in the backward pass using the ctx.save_for_backward method.
        """
        ctx.save_for_backward(input)
        return 0.5 * (5 * input ** 3 - 3 * input)

    @staticmethod
    def backward(ctx, grad_output):
        """
        In the backward pass we receive a Tensor containing the gradient of the loss
        with respect to the output, and we need to compute the gradient of the loss
        with respect to the input.
        """
        input, = ctx.saved_tensors
        return grad_output * 1.5 * (5 * input ** 2 - 1)

forward 메소드와 backward 메소드는 각각 다음과 같은 역할을 하게 됩니다.

forward : 순전파 단계에서 입력 Tensor( $x$ )를 저장하고 그 결과( $P(x)$ )를 출력합니다.
backward : 축적되어 온 Gradient와 순전파 단계에서 저장된 Tensor( $x$ )를 기반으로 연산에 맞는 Gradient( $P'(x)$ )를 전달합니다.

그럼 위 클래스를 적용하게 되면 어떤 결과를 보이는지 확인해보겠습니다.

x= torch.tensor([1.],requires_grad=True)
print(x.data, x.is_leaf, x.grad, x.grad_fn, x.requires_grad)
# > tensor([1.]) True None None True

y = LegendrePolynomial3.apply(x) # apply를 통해 grad 연산을 적용
print(y.data, y.is_leaf, y.grad, y.grad_fn, y.requires_grad)
# > tensor([1.]) False None <torch.autograd.function.LegendrePolynomial3Backward object at 0x000002027AEB7740> True

print(y.grad_fn.next_functions)
# > ((<AccumulateGrad object at 0x000002027B579DC0>, 0),)

y.backward()

print(x.data, x.is_leaf, x.grad, x.grad_fn, x.requires_grad)
# > tensor([1.]) True tensor([6.]) None True

print(y.data, y.is_leaf, y.grad, y.grad_fn, y.requires_grad)
# > tensor([1.]) False None <torch.autograd.function.LegendrePolynomial3Backward object at 0x000002027AEB7740> True

이 과정에서 grad_fn의 역할을 확인하기 위해 네가지의 포인트를 확인해야합니다.

순전파 과정에서 y.grad_fn 을 확인해보면 <torch.autograd.function.LegendrePolynomial3Backward object at 0x000002027AEB7740>를 확인할 수 있고 이는 grad_fn으로 직접 선언한 Polynomial3가 선언된 것을 확인할 수 있습니다.
순전파 과정에서 y.grad_fn.next_functions 를 확인해보면 ((<AccumulateGrad object at 0x000002027B579DC0>, 0),)로 보아 입력은 하나이고 leaf Tensor이기 때문에 AccumulateGrad가 지정되어 있는 것을 확인할 수 있습니다.
순전파 과정에서 y.data를 확인해보면 tensor([1.])으로 $P(1)=\frac{1}{2}(5(1)^3-3(1))=1$ 이 출력되는 것을 확인할 수 있습니다.
역전파 y.backward() 이후의 x.grad를 확인해보면 $P'(1)=\frac{3}{2}(5(1)^2 -1)=6$ 이 나오는 것을 확인할 수 있습니다. (grad_output=1 이므로[기본값])

즉, grad_fn에서는 순전파 과정과 역전파 과정에대한 연산 정보가 담겨있고, ctx를 기반으로 연산의 입력에 대해 다루게 되며, next_functions의 내용을 기반으로 계산된 Gradient를 전달하게 됩니다.

그렇다면 이렇게 계산된 Gradient를 전달하는 과정에 대해서 다음 절에서 더 자세히 다루겠습니다.

역전파 과정

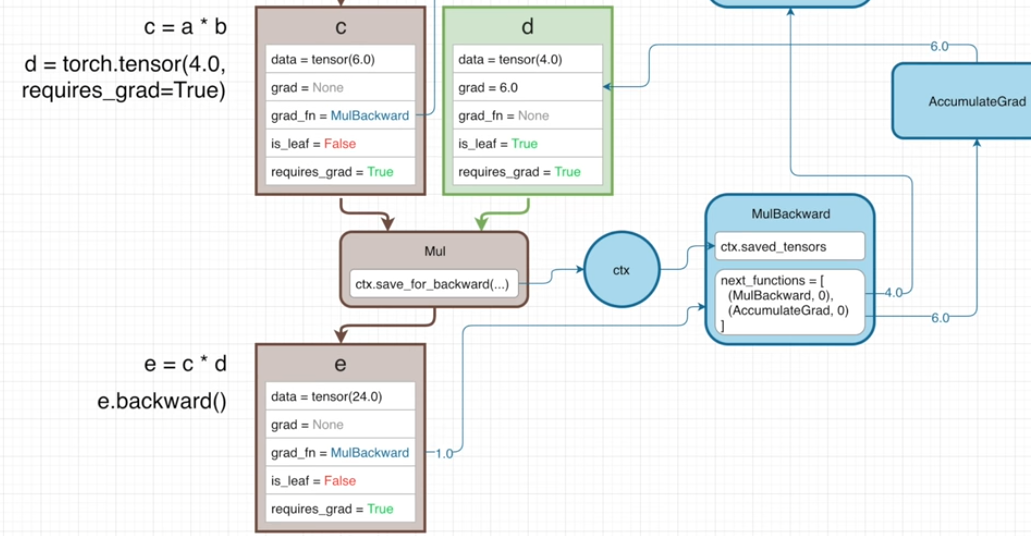
역전파 과정에서 Gradient를 전달하는 과정을 설명하기 위해 다음과 같이 $c = a \times b,d=c \times d$ 두개의 식을 통해 설명하겠습니다.

c = a \times b

e = c \times d

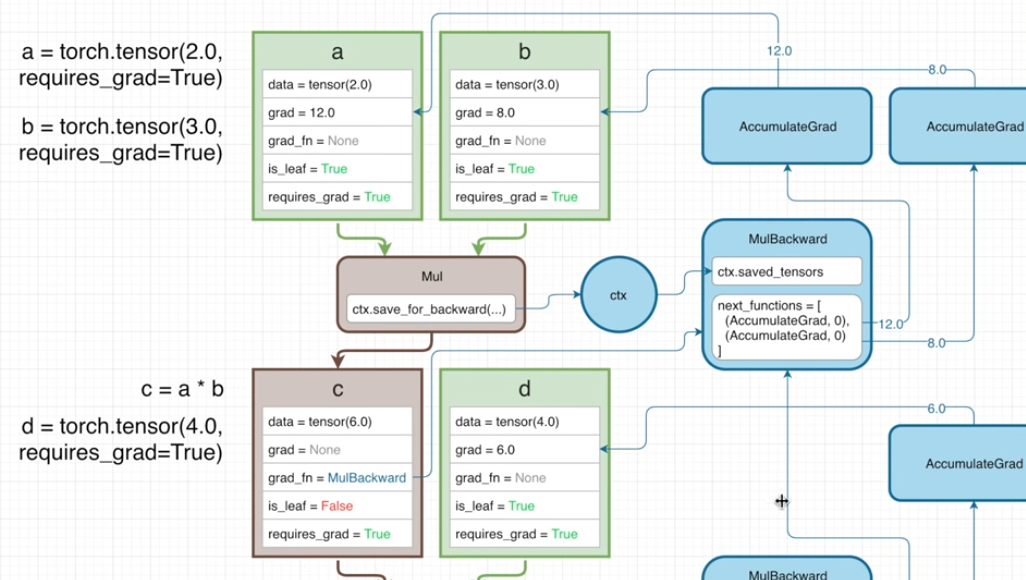
기본적인 연산의 흐름은 이전에 보았던 Tensor 연산과 크게 다르지 않습니다.

다른 점은 다음과 같습니다.

Tensor b의 requires_grad 가 True가 되었고 이에 따라 c의 grad_fn의 next_functions의 두번째 튜플이 None이 아닌 AccumulateGrad 객체를 갖고 있다는 것
Tensor c와 Tensor d와의 곱연산으로 생성된 Tensor e의 grad_fn의 next_functions의 첫번째 튜플은 AccumulateGrad가 아닌 MulBackward 객체를 갖고 있는 것

이러한 연산 그래프가 주어진다고 할 때 e.backward() 메소드를 실행하여 역전파를 진행한다고 할때 다음과 같이 진행됩니다.

e.backward()를 실행하면서 Gradient는 1로 기본값으로 e의 grad_fn인 MulBackward 전달합니다.

MulBackward 객체는 다음과 같은 backward() 메서드를 실행하여 Gradient를 반환합니다.

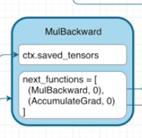
@staticmethod
def backward(ctx, grad_output):
	# grad_output = 1로 들어옴
    x1, x2 = ctx.saved_tensors # x1 = c, x2 = d
    return grad_output*x2, grad_output*x1 # c에 전달할 Gradient(=4), d에 전달할 Gradient(=6)

계산된 Gradient를 next_functions에 있는 객체로 전달합니다.
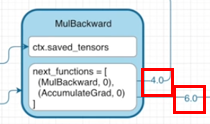
전달받은 Gradient를 통해 다음 연산을 진행합니다. [c:MulBackward, d:AccumulateGrad]

4-1. MulBackward 객체는 이전과 동일한 backward() 메서드를 실행하여 Gradient를 반환합니다.
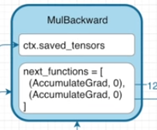
```
	@staticmethod
    def backward(ctx, grad_output):
        # grad_output = 4로 들어옴
        x1, x2 = ctx.saved_tensors # x1 = a, x2 = b
        return grad_output*x2, grad_output*x1 # c에 전달할 Gradient(=4*3), d에 전달할 Gradient(=4*2)
```
4-2. AccumulateGrad 객체는 전달받은 Gradient를 기반으로 d의 grad에 저장합니다.
4-1에서 계산된 Gradient를 next_functions에 있는 객체로 전달합니다.
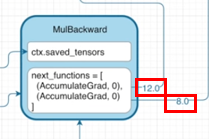
전달받은 Gradient를 통해 다음 연산을 진행합니다. [a:AccumulateGrad, b:AccumulateGrad]

6-1. AccumulateGrad 객체는 전달받은 Gradient를 기반으로 a의 grad에 저장합니다.

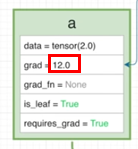
6-2. AccumulateGrad 객체는 전달받은 Gradient를 기반으로 b의 grad에 저장합니다.
더 이상 전달될 Gradient가 없으므로 종료합니다.