선형 결합

선형 결합(線型 結合, linear combination) 또는 일차 결합(一次 結合)은 수학에서 각 항에 상수를 곱하고 결과를 더함으로써 일련의 항으로 구성된 표현식이다(예: x와 y의 선형 결합은 ax + by 형식인데 여기서 a와 b는 상수이다). (위키백과)

선형 대수학에서는 위 수식을 다음과 같이 표현한다.

$a$는 실수 전체의 값을 의미하며 $\overrightarrow{v}$는 벡터를 의미한다.

즉, 모든 벡터의 값을 조정(scale)하고 더하여 하나의 벡터를 얻어내는 것이다.

예시

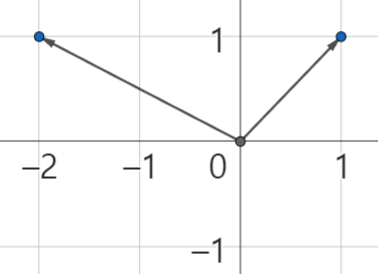
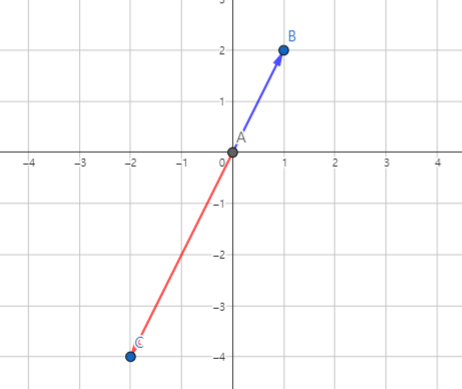
가령 다음의 두 벡터 $\overrightarrow{v_1}= (1,1)$ 과 $\overrightarrow{v_2} = (-2,1)$를 통해 예를 든다 표현한다고 해보자.

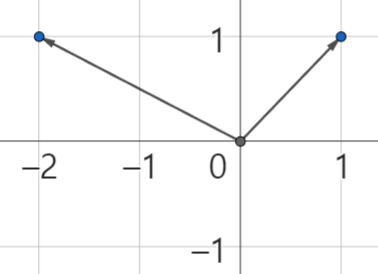
두 벡터를 $a_1 , a_2 = 1, 1$로 선형 결합을 하는 경우는 다음과 같다.

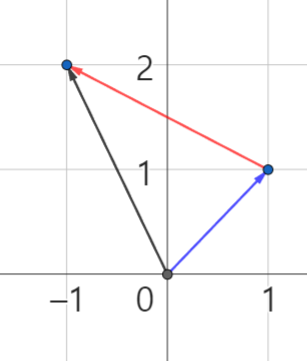
원점에서 시작해 벡터 $\overrightarrow{v_1}$의 1배만큼 이동한 끝 점 $(1,1)$에서 벡터 $\overrightarrow{v_2}$의 1배만큼 이동한 위치가 $(-1,2)$이며 두 벡터의 합은 원점에서 $(-1,2)$을 가리키는 하나의 벡터가 되는 것이다.

선형 결합의 집합

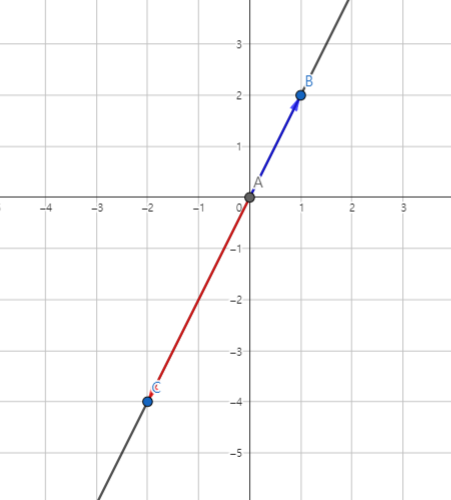
위에서는 $a$를 상수인 1로 고정하여 선형 결합을 하였다.

그렇다면, $a_1=1$인 상황에서 $a_2=k(k$는 실수 전체$)$가 되는 경우 두 벡터의 선형 결합은 어떻게 될까?

$x,y$ 좌표 관계를 $k$값을 통해 1차식으로 다음과 같이 직선으로 표현할 수 있게 되었다.

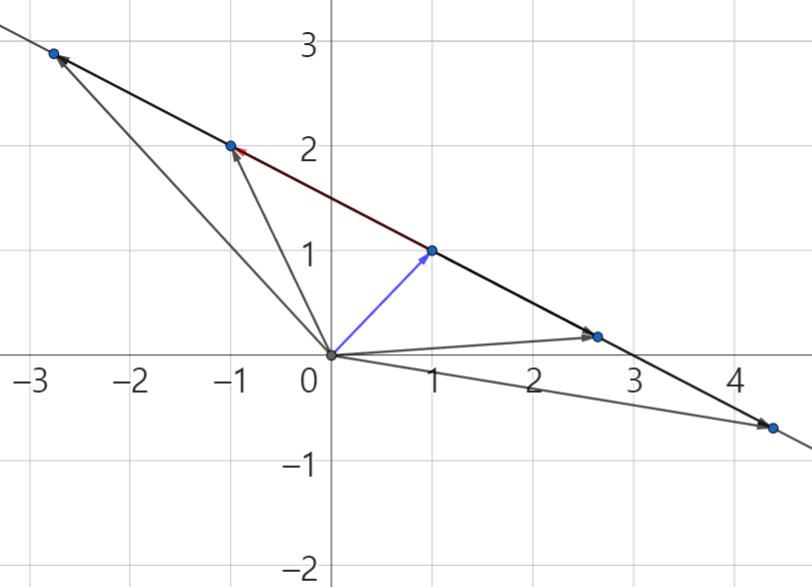
위와 같이 $\overrightarrow{v_1} + k\overrightarrow{v_2}$의 선형 결합으로 생긴 벡터의 끝 점들의 집합은 결국 하나의 직선 공간을 모두 표현할 수 있게 된다.

두 벡터의 평면 공간 표현

위의 결과는 $a_1$을 1로 고정하여 선형결합으로 얻어낸 끝점들의 집합으로 하나의 직선이다.

그렇다면 $a_1$을 $k'(k'$은 실수 전체$)$로 둔다면 어떻게 될까?

해당 직선을 벡터 $\overrightarrow{v_1}$의 방향으로 평행이동 시키는 것이며, 이 직선들의 집합은 결국 하나의 면이 된다.

즉, 두 벡터의 선형 결합을 통해 2차원 평면에 존재하는 모든 벡터들을 표현할 수 있다는 것이다.

이렇게 두 벡터의 선형 결합을 통해 만들어 내는 것을 Span(생성)이라고 한다.

---

Span(생성)

선형생성(線型生成, linear span) 또는 선형포(線型包, linear hull)는 선형대수학 또는 함수해석학에서 어떤 벡터공간이 모든 부분공간의 교집합일 때 그 벡터공간의 벡터의 집합이다. 고로 벡터들의 집합의 선형생성은 선형공간이다. (위키백과)

앞에서 두개의 벡터를 선형 결합 통해 얻어낸 벡터들의 집합이 2차원 평면의 모든 벡터를 표현 할 수 있고 이를 Span이라고 하였다.

그렇다고 '두개의 벡터는 항상 2차원 벡터 공간을 형성 하는구나' 라고 급하게 판단해서는 안된다.

반례

• $\overrightarrow{v_1} = (0,0) , \overrightarrow{v_2}= (0,0)$인 경우

이 경우에는 선형 결합을 한다고 하여도 항상 $(0,0)$이 나오기 때문에 결국 하나의 점에 대한 공간만을 나타낸다.

• $\overrightarrow{v_1} = (1,2) , \overrightarrow{v_2} = (-2,-4)$인 경우

이 경우에는 $\overrightarrow{v_2} = -2 \times \overrightarrow{v_1}$이다. 이를 이용해 선형 결합을 수식으로 나타내면 다음과 같다.

$x,y$의 좌표 관계를 $(a_1-2a_2)$를 통해 1차식으로만 표현이 가능하고 이를 나타내면 벡터공간이 다음과 같이 2차원 평면이 아닌 하나의 직선임을 알 수 있다.

벡터공간

선형대수학에서 벡터 공간(vector空間, 영어: vector space, 문화어: 벡토르공간, 선형공간[1][2]) 또는 선형 공간(線型空間, 영어: linear space)은 원소를 서로 더하거나 주어진 배수로 늘이거나 줄일 수 있는 공간이다. (위키 백과)

벡터 공간과 Span은 비슷한 개념처럼 보일 수는 있으나 다르다.

벡터공간 정의

벡터의 요소가 $(x,y,z)$이고 $x,y,z$는 임의의 실수라고 할 때 이 벡터들의 집합은 3차원의 공간을 형성할 수 있고 이를 벡터 공간이라 한다.

Span 정의

벡터들의 선형 결합을 통해 만들 수 있는 모든 벡터들을 통해 특정 공간을 생성하는 것이다. 같은 요소를 가지고 생성한 공간은 벡터 공간이 될 수도 있고(예시) 그보다 작은 공간이 될 수도 있다.(반례)

---

Basis(기저)

선형대수학에서, 어떤 벡터 공간의 기저(基底, 영어: basis)는 그 벡터 공간을 선형생성하는 선형독립인 벡터들이다. 달리 말해, 벡터 공간의 임의의 벡터에게 선형결합으로서 유일한 표현을 부여하는 벡터들이다. (위키백과)

기저에 대한 정의에서 선형 결합, 벡터 공간에 대해 들어봤지만 선형 독립이라는 얘기는 하지 않았다.

그렇다면 선형 독립이란 무엇일까?

선형독립과 선형종속

선형대수학에서 일차 독립 집합(一次獨立集合, 영어: linearly independent set) 또는 선형 독립 집합(線型獨立集合)은 모든 벡터가 남은 벡터들의 일차 결합으로 나타낼 수 없는 벡터들의 집합이다.(위키백과)

아래 식을 통해 다시 설명하면 다음과 같다.

위 식에서 위를 만족하는 $a$값이 0 뿐이라면 벡터들은 선형 독립이라고 할 수 있습니다.

반면에 위 식에서 위를 만족하는 $a$값이 무수히 많다면 해당 벡터들은 선형 종속이라고 할 수 있습니다.

예시

벡터 공간이 2차원인 두가지 경우는 다음과 같다.

벡터가 선형종속인 경우

$a_1\overrightarrow{v_1}+a_2\overrightarrow{v_2}=0$에서 $a$값이 무수히 많기 때문에 선형 종속인 관계이다.

이 두 벡터를 통해 Span을 하는 경우 1차원의 공간을 생성할 수 있다.

또한 $\overrightarrow{v_1}$에 종속 관계인 임의의 어떤 벡터 $\overrightarrow{v_n} = (k,0)$을 추가하여 선형 결합을 한다고 하여도 X축에 평행한 직선만을 표현할 수 있다.

즉, 현재의 벡터 집합에 어떤 선형 종속인 벡터를 추가한다 하여도 벡터 공간의 차원이 늘어나지 않는다.

벡터가 선형 독립인 경우

$a_1\overrightarrow{v_1}+a_2\overrightarrow{v_2}=0$에서 $a$값이 모두 0이어야 하기때문에 선형 독립인 관계이다.

이 두 벡터를 통해 Span을 하는 경우 2차원의 공간을 생성할 수 있다.

벡터 공간(2차원)을 생성할 수 있으므로 두 벡터는 기저라고 할 수 있다.