ViTPose 논문 리뷰

김태훈·2023년 7월 15일

Computer Vision Deep Learning ViT paper-review pose estimation

본 페이지에서는 ViTPose: Simple Vision Transformer Baselines for Human Pose Estimation논문에 대해서 말하고자 합니다.

1. Intro

Vision Transformer의 발전은 그동안 Computer Vision 분야에서 여러 작업에 대해서 SOTA를 달성할 수 있게 하였습니다.

이런 발전 경향성에서 자세 추정(Pose Estimation) 작업에도 Vision Transformer를 적용하는 여러 방법들이 있는데 다음과 같습니다..

CNN을 BackBone으로 사용하며 추출된 특징을 Transformer에 사용하는 방법 (TokenPose,TransPose)
Keypoint들의 위치를 잘 찾아내기 위해서 Encoder와 Decoder를 통합하는 방법 (PRTR)
Transformer를 직접적으로 특징들을 추출하도록 하고 복잡한 구조를 통해 성능을 높이는 방법 (HRFormer)

이런 여러 방법들은 자세 추정 방식에서 좋은 성능을 내는 것은 맞으나 모두 특징 추출을 위해 CNN을 사용하거나 복잡한 구조를 가지고 있다는 특징이 있습니다.

따라서 본 논문은 다음과 같은 질문을 하며 순수한 ViT를 자세 추정 작업에 적용하고자 했습니다.

How well can the plain vision transformer do for pose estimation?

ViTPose는 다음과 같은 관점으로 ViTPose의 장점을 얘기합니다.

모델 구조의 간단함
모델 크기의 다양함
학습에서의 유연성
학습 내용에 대한 전이가능성

특히 본 논문은 모델 구조의 간단함을 주의 깊게 살펴봅니다.

2. ViTPose

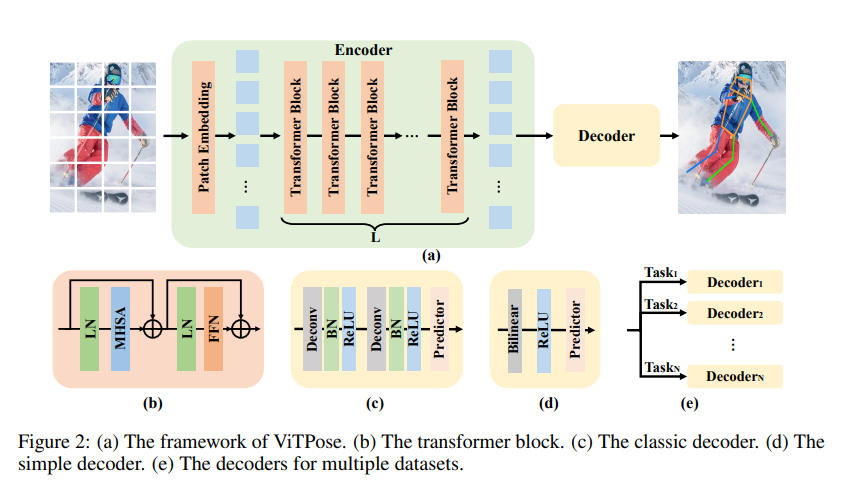
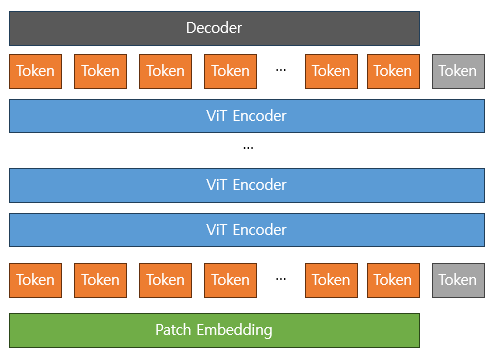
위의 사진은 ViTPose의 모델 구조로 기존의 ViT의 CLS 토큰과 Decoder를 제외하면 동일하다고 할 수 있습니다.

2.1 모델 구조의 간단함

Encoder

본 논문에서 강조하는 점은 ViTPose는 다른 복잡한 구조를 사용하지 않고 ViT와 간단한 Decoder를 활용하여 좋은 성능을 냈다는 것입니다.

구조적 간단함을 위해 Skip connection이나 Cross Attention 등의 방법들은 사용하지 않았다고 합니다.

모델의 동작 과정은 ViT와 동일하며 다음과 같습니다.

MHSA와 FFN은 각각 Multi Head Self Attention , Feed Foward Network를 의미합니다.

또한 $i$ 는 $i$ 번쨰 Transformer 레이어를 말하며 $F_0$ 는 Patch Embedding 레이어를 말합니다.

F'_{i+1} = F_i + MHSA(LN(F_i)), F_{i+1} = F'_{i+1}+FFN(LN(F'_{i+1}))

입력이미지 - $X \in \R^{H \times W \times 3}$

Patch Embedding 레이어 출력 - $F_0 \in \R^{(\frac{H}{d} \times \frac{W}{d}) \times C}$ ( $d$ 는 Patch의 크기를 의미합니다.)

Encoder의 최종 출력 - $F_n \in \R^{(\frac{H}{d} \times \frac{W}{d}) \times C}$

Decoder

Decoder는 각 관절에 대한 Heatmap을 표현하기 위해서 두가지 방법을 제안합니다.

Deconvolution을 사용하는 방법(Classic Decoder)

두개의 Deconvolution으로 이루어져 있으며 Deconvolution 이후에는 Batch Normalization , ReLU을 적용하는 방법

K = Conv_{1 \times 1}(Deconv(Deconv(F_{out})))

Simple Decoder

추출된 특징들을 4 Scale로 Upsample을 한 뒤에 ReLU를 적용하고 3 $\times$ 3 Convolution을 적용하는 방법(공식 코드에서는 아래가 맞습니다.)

K = Conv_{3 \times 3}(ReLU(Bilinear(F_{out})))

이때 $K \in \R^{\frac{H}{4} \times \frac{W}{4} \times N_k}$ 이며 $N_k$ 는 관절의 개수입니다.

이런 간단한 구조의 Decoder로도 좋은 성능을 냈다고 합니다.

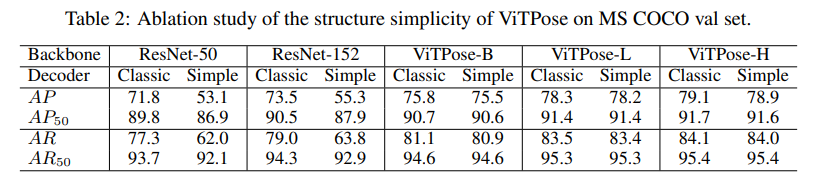
위는 Decoder에 따른 ResNet과 ViT의 성능표인데 여기서 주목할 점은 Simple Decoder와 Classic Decoder사이의 성능 차이입니다.

바로 ResNet은 두 Decoder 사이에 성능 차이가 매우 큰 반면에 ViTPose에서는 성능 차이가 별로 없다는 것입니다.

이는 ViTPose가 특징을 추출하는 능력이 매우 좋으며 이에 따라 복잡한 구조의 Decoder가 필요 없음을 의미합니다.

2.2 모델 크기의 다양성

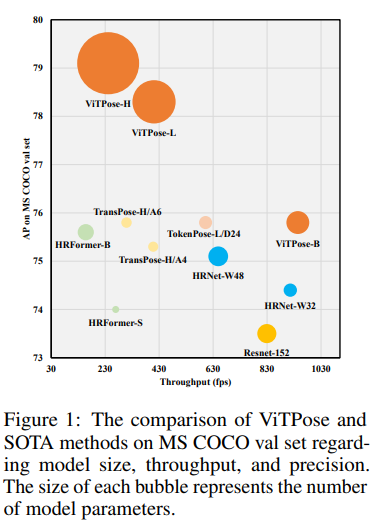
ViTPose의 모델 구조의 간단함 때문에 위의 사진 처럼 여러 모델 크기를 선택할 수 있게 되었다고 합니다.

특히 모델 구조의 큰 변경 없이 레이어의 수나 채널의 수만 변경하여 모델을 쉽게 다양하게 구현할 수 있다고 합니다.

2.3 학습에서의 유연성

사전학습에서의 유연성

ViT 의 특성상 많은 양의 데이터를 학습함으로써 좋은 성능을 내게 됩니다.

이러한 특성 때문에 쉽게 사전학습을 위해서 MAE(Masked AutoEncoder) 방법을 사용해 사전학습을 진행합니다.

여기서 MAE란 Patch의 일부를 마스킹 하면서 Encoder의 끝 부분에서 마스킹 된 부분을 추측하도록 하는 방식입니다.

해상도에서의 유연성

해상도에서의 유연성이라고 하면 다음의 두가지 방법이 있습니다.

Downsampling Ratio $d$ (패치 크기)를 적절히 지정하여 입력 이미지에 대해 적절히 처리할 수 있음.
고해상도 이미지를 다루기 위해 입력 이미지를 Resize하고 패치로 나누어 학습할 수 있음.

$d$ 를 조절하기 위해 Patch Embedding 레이어에서 Stride를 패치 크기의 일부분으로 바꾸고 겹치도록 진행한다.(ViT의 Hybrid Embedding을 사용하는 듯 합니다.)

위의 테이블에서 주목할 점은 1번째와 2번째 열의 픽셀 수와 성능입니다.

각각의 픽셀 수는 150,528개와 147,356개 입니다.

당연히 픽셀 수가 더 많은 전자가 성능이 더 좋아야 일반적이지만 반대로 후자가 성능이 더 좋습니다.

이 이유에 대해서 저자는 MS COCO 데이터셋 이미지에서 사람의 비율이 4:3이기 때문일 것이라고 합니다.

Attention 유형에 대한 유연성

이미지 전체에 대해서 Attention을 수행하는 경우(패치 크기가 1인 경우) Computational Cost가 크게 발생합니다.

Position Embedding을 추가한 Window 기반 Attention(기존 ViT 기법)은 Computational Cost가 줄어들긴 했지만 Global Context에 대한 정보가 적기 때문에 성능이 감소할 수 있습니다.

이를 해결하기 위해서 두가지 방법을 제안하는데 다음과 같습니다.

아래의 방법론들에 대한 자세한 설명은 나중에 새로운 글에서 다루겠습니다.

Shift Window (Swin Transformer에서 제안된 기법)

고정된 Window Attention 방법 대신 Shift연산을 통해 인접 Window에 정보가 흐를 수 있도록 하는 방법이다.

Pooling Window(MViT,ViTDet에서 제안된 기법)

Shift Window 방법과는 다르게 Pooling 방법을 통해 정보가 흐를 수 있도록 하는 방법이다.

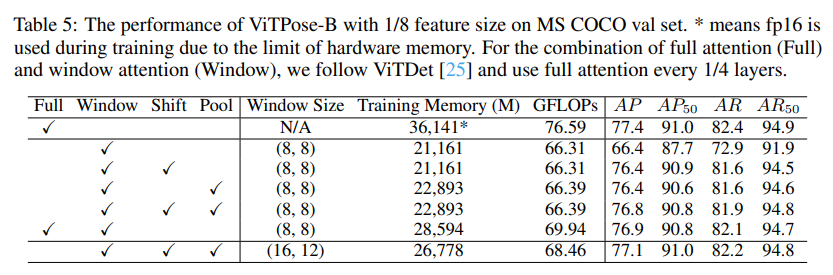
위의 사진은 Attention 기법에 따른 성능 표인데 주목할 점은 패치 크기를 8로 한 후 Shift Window Attention을 할 경우 적은 연산량으로 Full Attention과 매우 비슷한 성능을 내는 것을 볼 수 있습니다.

Fine Tuning에 대한 유연성

NLP에서도 증명이 됐듯이 ViTPose는 사전 학습후 Fine Tuning을 하면 좋은 성능을 냈습니다.

위의 표는 Fine Tuning을 하는 레이어에 따른 성능 표입니다.

Task에 대한 유연성

Decoder의 구조가 간단하기 때문에 다양한 자세 추정을 위해서 구조를 어렵게 바꿀 필요 없이 동일한 Encoder를 가지고 여러 자세 추정 데이터에 맞게 Heatmap들을 구성할 수 있다고 합니다.

2.4 학습 내용에 대한 전이성

전이학습의 방법 중 하나는 잘 학습된 큰 모델을 작은 모델에게 모방 하도록 학습하는 것인데 이를 Distillation 방법이라고 합니다.

잘 학습 된 모델을 선생님이라고 하고 학습 해야할 작은 모델을 학생이라고 예를 들어 설명합니다.

선생님의 출력을 $K_t$ 학생의 출력을 $K_s$ 라고 한다면 전이학습을 위한 Loss식은 다음과 같습니다.

L^{od}_{t->s} = MSE(K_s,K_t)

본 논문에서는 출력의 결과만 동일하도록 전이하는 것이 아닌 토큰-Based Distillation 방식을 소개합니다.

그 방법은 다음과 같습니다.

학습가능한 Knowledge 토큰 $t$ 를 무작위로 초기화 한다.
Teacher Model의 Patch Embedding 레이어 이후에 Visual 토큰에 Append한다. (여기서 Visual 토큰이라 함은 기존의 토큰들을 의미합니다.)
잘 학습된 Teacher 모델의 파라미터 들을 Freeze하고 Knowledge 토큰을 학습시킨다.

t^* = \displaystyle{\underset{t}{argmin}}(MSE(T({t;X})),K_{gt})

$K_{gt}$ 는 Heatmap Label이고 $X$ 는 입력 이미지 $T({t;X})$ 는 Teacher Model의 Prediction $t^*$ 는 loss를 최소화하는 Optimal한 토큰이다.

이후 $t^*$ 를 Frozen 후 Student Model 내의 Visual 토큰과 함께 Concatanate 하여 전이학습을 진행한다.

따라서 최종적인 Loss함수는 다음과 같다.

L^{td}_{t->s} = MSE(S({t^*;X}),K_{gt}), or L^{tod}_{t->s} = MSE(S({t^*;X}),K_t)+ MSE(S({t^*;X}),K_{gt})

$L^{td}_{t->s}$ , $L^{tod}_{t->s}$ 는 각각 Token Distillation Loss와 출력 Distillation과 Token Distillation Loss의 조합이다.

3. 추가 설명

Token Based-Distillation

내용을 말로 하면 이해가 잘 안되지만 그냥 CLS 토큰 개념이라고 보시면 됩니다.

잘 학습 된 ViTPose 모델이 있다고 할 때 토큰 끝에 새로운 토큰이 들어간다고 하면 기존의 토큰들은 새로운 토큰하고 Attention을 하게 됩니다.

이 과정에서 기존의 토큰들을 모두 Freeze하게 되면 결국 새로운 토큰만 학습되게 되면서 전체 토큰과의 관계를 잘 설명할 수 있는 하나의 토큰이 되며 이는 위에서 말한 $t^*$ 가 됩니다.

이후 이 토큰 $t^*$ 를 Student Model에 넣어 기존 Distillation 방법을 진행합니다.

기존의 Distillation 방법이 정답만 맞으면 돼 하고 알려주는 것이라면 Token Based Distillation은 정답 뿐이 아닌 문제 해결 방법도 같이 제공한다고 볼 수 있습니다.

L^{td}_{t->s} = MSE(S({t^*;X}),K_{gt}), or L^{tod}_{t->s} = MSE(S({t^*;X}),K_t)+ MSE(S({t^*;X}),K_{gt})

위 수식의 의미를 하나하나 살펴보면 다음과 같습니다.

L^{td}_{t->s} = MSE(S({t^*;X}),K_{gt})

학생에게 풀이 방법( $t^*$ )을 알려주고 문제의 답( $K_{gt}$ )와 비교해 채점( $MSE$ )한다.

L^{tod}_{t->s} = MSE(S({t^*;X}),K_t)+ MSE(S({t^*;X}),K_{gt})

학생에게 풀이 방법( $t^*$ )을 알려주고 문제의 정답 $K_{gt}$ 뿐이 아닌 선생님의 정답 $K_{t}$ 를 이용해 채점( $MSE$ )한다.

4. 코드구현

PyTorch


class Patch_Embedding(nn.Module):
    def __init__(self,in_channels,height,width,patch_size,d_model):
        super(Patch_Embedding,self).__init__()
        self.p = patch_size
        self.c = in_channels
        self.h = height
        self.w = width

        self.projection = nn.Linear(in_channels*patch_size**2,d_model)
        self.positional_encoding = nn.Parameter(torch.zeros((height*width)//(patch_size**2),d_model))
    
    def patchify(self,x):
        out = img.reshape(-1,self.c,self.h//self.p,self.p,self.w//self.p,self.p) # b,c,h//p,p,w//p,p
		out = out.permute(0,2,4,1,3,5) # b, h//p,w//p,c,p,p
        out = out.reshape(-1,self.n,self.c*self.p*self.p) # b,n,cpp
        return out
    
    def forward(self,x):
        out = self.patchfy(x)
        out = self.projection(out)
        
        out += self.positional_encoding
        return out
    
class Hybrid_Embedding(nn.Module):
    def __init__(self,in_channels,height,width,patch_size,d_model):
        super(Hybrid_Embedding,self).__init__()
        self.conv = nn.Conv2d(in_channels,d_model,patch_size,patch_size)
        self.positional_encoding = nn.Parameter(torch.zeros((height*width)//(patch_size**2),d_model))
        
    def forward(self,x):
        out = self.conv(x).flatten(2).transpose(1,2)
        out += self.positional_encoding
        return out

class MHA(nn.Module):
    def __init__(self,d_model,d_k,d_v,num_head):
        super(MHA,self).__init__()
        
        self.h = num_head
        self.d_k = d_k
        self.d_v = d_v
        
        self.q_linear = nn.Linear(d_model,d_k*num_head)
        self.k_linear = nn.Linear(d_model,d_k*num_head)
        self.v_linear = nn.Linear(d_model,d_v*num_head)
        
        self.MHA_linear = nn.Linear(d_v*num_head,d_model)
        
    def forward(self,x):
    #n x d_model nxn nxd_v nx d_v
        q = self.q_linear(x).view(x.size(0),x.size(1),self.h,self.d_k).transpose(1,2)
        k = self.k_linear(x).view(x.size(0),x.size(1),self.h,self.d_k).transpose(1,2)
        v = self.v_linear(x).view(x.size(0),x.size(1),self.h,self.d_v).transpose(1,2)

        matmul1 = torch.einsum("...nd,...kd->...nk",q,k)

        softmax = torch.softmax(matmul1/np.sqrt(self.d_k),-1)
        
        matmul2 = torch.einsum("...nd,...dk->...nk",softmax,v)

        concat = matmul2.transpose(1,2)
        concat = concat.reshape(concat.size(0),concat.size(1),self.h*self.d_v)

        out = self.MHA_linear(concat)
        return out
    
class Encoder(nn.Module):
    def __init__(self,d_ff,d_model,d_k,d_v,num_head):
        super(Encoder,self).__init__()
        self.MHA = MHA(d_model,d_k,d_v,num_head)
        self.MLP = nn.Sequential(
            nn.Linear(d_model,d_ff),
            nn.ReLU(),
            nn.Linear(d_ff,d_model)
        ) 
        self.ln = nn.LayerNorm(d_model)
        
        
    def forward(self,x):
        out_MHA = self.ln(x)
        out_MHA = self.MHA(out_MHA)
        
        out_MHA += x
        
        out_MLP = self.ln(out_MHA)
        out_MLP = self.MLP(out_MLP)
        
        out_MLP += out_MHA
        
        return out_MLP

    
    
class ViTpose(nn.Module):
    def __init__(self,num_layer,height,width,in_channels,out_channels,patch_size,d_model,d_ff,d_k,d_v,num_head,hybrid=False,simple_head=True):
        super(ViTpose,self).__init__()
        if hybrid:
            self.Embedding = Hybrid_Embedding(in_channels,height,width,patch_size,d_model)
        else :
            self.Embedding = Patch_Embedding(in_channels,height,width,patch_size,d_model)
        
        self.hp = height//patch_size
        self.wp = width//patch_size
        
        layers = []
        
        for i in range(num_layer):
            layers.append(Encoder(d_ff,d_model,d_k,d_v,num_head))
        
        self.Encoder = nn.Sequential(*layers)
        
        self.ln =  nn.LayerNorm(d_model)
        
        if simple_head :
            self.heatmap_head = nn.Sequential(
                nn.Upsample(scale_factor=4,mode='bilinear'),
                nn.ReLU(),
                nn.Conv2d(d_model,out_channels,3,1,1)
            )
        else:
            self.heatmap_head = nn.Sequential(
                nn.ConvTranspose2d(d_model,d_model,2,2), 
                nn.BatchNorm2d(d_model),
                nn.ReLU(),
                nn.ConvTranspose2d(d_model,d_model,2,2),
                nn.BatchNorm2d(d_model),
                nn.ReLU(),
                nn.Conv2d(d_model,out_channels,1,1)
            )

    def forward(self,x):
        
        out = self.Embedding(x)
        out = self.Encoder(out)
        
        out = self.ln(out)
        out = out.permute(0,2,1).reshape(out.size(0),-1,self.hp,self.wp)
        
        heatmap = self.heatmap_head(out)
        
        return heatmap

김태훈

👋 인공지능을 통해 다음 세대가 더 나은 삶을 살도록

이전 포스트

선형 대수학 - 선형 결합, 생성, 벡터 공간, 선형독립, 기저

다음 포스트