Big O

GoldenDusk·2023년 8월 14일

BigO

알고리즘 공부

목록 보기

3/14

🍐자료구조와 알고리즘이 필요한 이유

1. 프로그래밍 언어란?

컴퓨터 프로그래밍에서 어떠한 알고리즘을 구현하기 위해서 쓰여지는 언어

자료구조와 알고리즘에 대한 이해가 있다면 구현하고자 하는 기능을 보다 쉽고 효울적으로 만들 수 있게 도와줌

현업의 경우 코딩테스트를 공부하지 않음 대부분은 언어나 프레임워크나 라이브러리에서 이미 잘 만들어진 아이들을 가져와서 만들고자 하는 기능을 가져와서 사용

2. 그렇다면 왜 코딩테스트를 볼까?

알고리즘 작성 후 질의/응답을 통해 자료구조와 알고리즘에 대해 얼마나 이해하고 있고 시간과 공간 복잡도에 대한 이해가 있는지 확인해보기 위함

EX.

하필 이 알고리즘을 선택한 이유는?
이것이 저것들의 비해 장단점은?
저것과 이것의 차이는?

🍐 알고리즘과 자료구조를 공부방법

자료 구조는 어느 상황에 쓰이는 것이 좋고 또 어떤 식의 API들이 있는지 이런 것들 조금 큰 그림을 보면서 공부

1. 자료구조

서비스나 어플리케이션에 필요한 데이터를 메모리에 어떻게 구조적으로 잘 정리해서 담아두고, 관리하고 효율적인 방식으로 필요한 데이터에 빠르게 접근하고 필요한 수정 삽입 삭제 할 수 있도록 도와준다. 기능에 적합한 알맞는 자료구조를 쓰는 것이 중요하다.

💡 자료 구조 공부시 Point

Order : 자료 구조 안에 있는 데이터들의 순서가 보장?
Unique : 중복된 데이터가 들어 갈 수 있는가?
Search : 검색에 얼마나 효율적인가?
Modification : 우리가 원하는 기능에 따라서 수정시 얼마나 효율적인지?

🍐 BigO

출처 : 니꼴라스 https://www.youtube.com/watch?v=BEVnxbxBqi8

1. 개요

알고리즘의 스피드를 어떻게 표현하는지 알아봄
빠르다, 느리다의 말이 아닌 CS지식

2. 알고리즘

제한된 공간과 시간 안에서 데이터를 어떻게 처리할 것인지를 정해놓은 로직

주어진 데이터를 검색하거나 정렬 또는 총점을 구하는 등의 다양한 계산을 할 수 있는 것을 말함

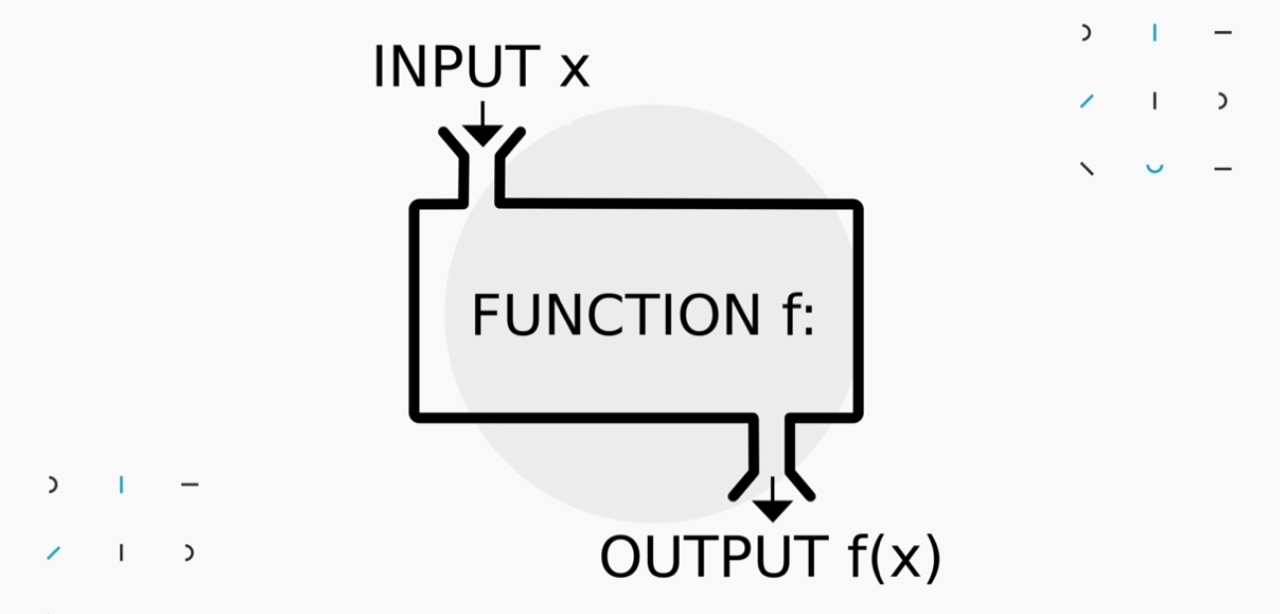
즉, 주어진 input으로 정의된 계산을 수행한 다음 output 결과값을 내는 것

3. 시간복잡도

💫 문제를 해결하는 데 걸리는 시간과 입력의 함수 관계

“빠르다”, “느리다”는 시간으로 표현하지 않음(시간 복잡도)
- 같은 알고리즘이라도 내 컴퓨터가 친구의 컴퓨터보다 빠를 수 있음
- 컴퓨터라는 하드웨어가 결정하기 때문
- “완료까지 걸리는 절차의 수”STEPS
- 알고리즘을 위해 필요한 연산의 횟수
- 특정 크기의 입력에 대하여 알고리즘이 얼마나 오래 걸리는지
선형 알고리즘의 경우 사이즈가 N개이면, N스텝이 필요함

4. 공간복잡도

공간복잡도 : 특정한 크기의 입력에 대하여 알고리즘이 얼마나 많은 메모리를 차지하는지
알고리즘을 위해 필요한 메모리의 양
예를 들어 int a[1004];라는 배열이면 a 배열은 1004X4바이트의 크기를 가지게 됨

5. Big O

💫 사이즈가 N개면, N스텝이 필요해요!!! 보다는 선형검색의 시간 복잡도 = O(N) 이렇게 설명하는 컨셉을 Big O

Big O란 시간복잡도를 표현하는 표기법
언제 무엇을 쓸지 빠르게 파악 가능하며, 자신의 코드를 평가 가능
- 왜..? 미래에 어떻게 작동할 수 있는지 알 수 있으니
- Big O를 이해시, 알고리즘을 빠르게 분석 가능, 언제 무엇을 쓸지 파악 가능
알고리즘의 퍼포먼스를 이해하기 쉽고 효율적으로 작성하는 방법

선형검색의 시간 복잡도 = O(N)
but, 항상 Big O가 모든 알고리즘을 완벽히 설명하는 것은 아님

배열을 인풋으로 사용할 함수, 인풋의 크기 상관없이 동일한 수의 스텝이 필요
- 아래의 코드는 print_first라는 파이썬 함수를 정의하며, 매개변수 arr에게 받으며, arr의 첫 번째 인덱스를 출력해냄
- 인덱스를 이용하여 한 번에 찾으니까
- 이 함수의 시간복잡도는 constant time(상수 시간) : N의 크기 상관없이 끝내는데 동일한 숫자의 스텝이 필요

def print_first(arr):
		print(arr[0])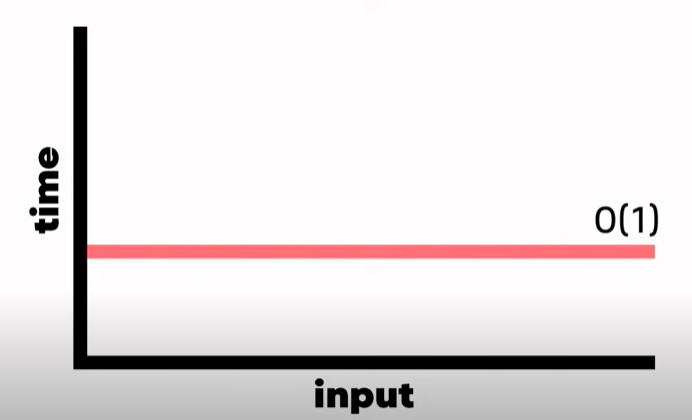

이 코드의 경우 2번의 print가 있는데 2개의 스텝이 필요한 것

def print_first(arr):
		print(arr[0])
		print(arr[0])

💫 이렇다면 O[2] 일까? NO! 여전히 O[1]

Big O는 함수의 디테일에 관심이 없고, 러프하게 어떻게 이 함수가 인풋의 사이즈에 따라서 어떻게 작동하는지가 중요
함수는 인풋 사이즈가 엄청나게 커져도 상관없이 미리 정해진 숫자에 따라 작동

즉, Big O는 큰 원리에만 관심을 가짐
꼭 기억해 둬야 할 것은 빅오는 상수를 신경 쓰지 않음

6. Constant Time Algorithm(상수 시간 알고리즘)

constant time (일정한 시간/상수)
인풋사이즈와 관계없이 스텝이 정해진 알고리즘들
항상 선호하는 것 ⇒ 인풋이 늘어나도 변하지 않음
현실적으로 항상 만들기 힘들다

O(n) 자바 코드로 나타내면

// 시간 복잡도 O(n)이 계산된다. O(1)
public class OneToSum {

    public int sum(int n){
        int sum = 0;

        return n * (n + 1) / 2;
    }


    public static void main(String[] args) {
       int n = 5;
       // static으로 주지 않을 때
       OneToSum object = new OneToSum();
       System.out.println(object.sum(10));
    }
}

7. 시간복잡도 1: Big O의 시간복잡도, 선형 시간 복잡도

배열의 사이즈가 10이라면, 10번 프린트 하는 함수 : O(N)

def print_all(arr):
	for n in arr:
		print(n)

Q: 만약 반복문을 두번이라면 O(2N)일까? ****

def print_all(arr):
	for n in arr:
		print(n)
	for n in arr:
		print(n)

A: 2는 상수이기에 버려두고, 여전히 O(N)으로 표현, 핵심은 변하지 않았지 때문

메세지가 같다 ⇒ 인풋이 증가하면 스텝도 선형적으로 증가

O(N)이나 선형 시간복잡도를 그래프

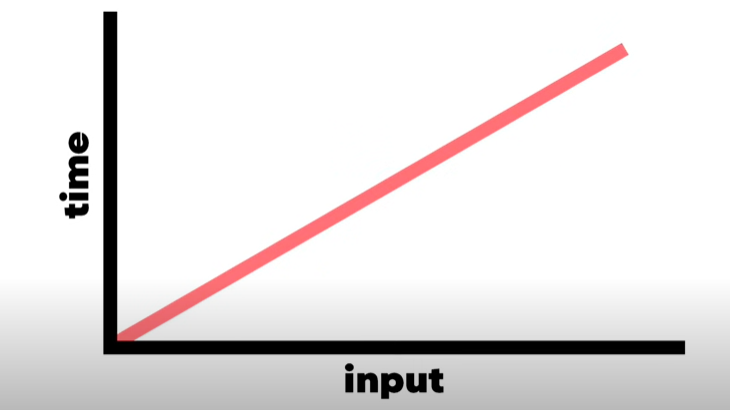
8. 시간복잡도 2 : Quadratic Time(2차 시간)

Nested Loops(중첩 반복)이 있을 때, 발생
아래의 경우 배열의 각 아이템에 대해 루프를 반복, 실행

def print_twice(arr)
	for n in arr:
		for x in arr:
			print(x, n)

시간복잡도 : 인풋 $n^2$ EX. 인풋이 10개시 100번의 스텝 : 루프 안의 루프에서 함수를 실행시키기 때문

2차 시간복잡도 그래프를 선형 시간복잡도와 비교 그래프

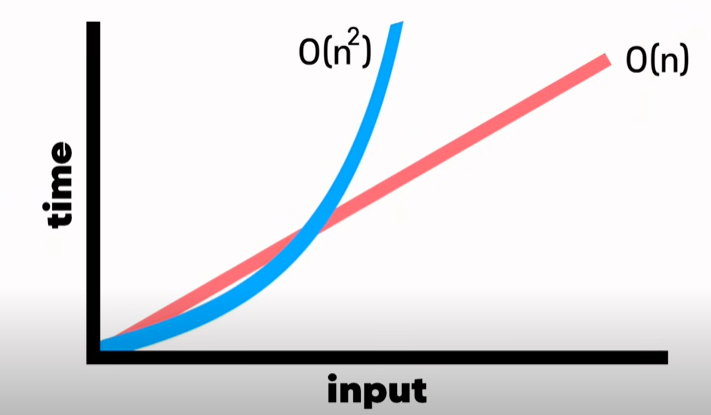
선형 시간복잡도가 2차 시간복잡도보다 더 효율적

9. 시간복잡도 3 : 로그 시간(Logarithmic Time)

이진검색 알고리즘 설명시 사용 ⇒ 얼마나 빠른지 설명 가능
1. 이진 검색 알고리즘은 인풋 사이즈가 2배가 되어도 필요한 step의 수는 1개밖에 안들어남
2. 왜냐? 이진검색은 각 프로세스의 스텝을 절반으로 나눠서 하기 때문이
표현법 : O(log N)
정렬된 배열에만 사용 가능
exponent(지수) ↔ logarithm(로그)

n = $log_232$ n은 32를 2로 몇번을 나눠야 1이 나올까?

💫 32 / 2 = 16 ← 1
16 / 2 = 8 ← 2
8 / 2 = 4 ← 3
4 / 2 = 2 ← 4
2 / 2 = 1 ← 5 times

n은 5 ⇒ 이진 검색과 같음 인풋을 반으로 나누고 시작하는 것처럼 ⇒ Big O의 특성상 n = $log32$ 아래의 2가 사라짐 ⇒ So, log N이 되는 것
로그 시간복잡도의 그래프

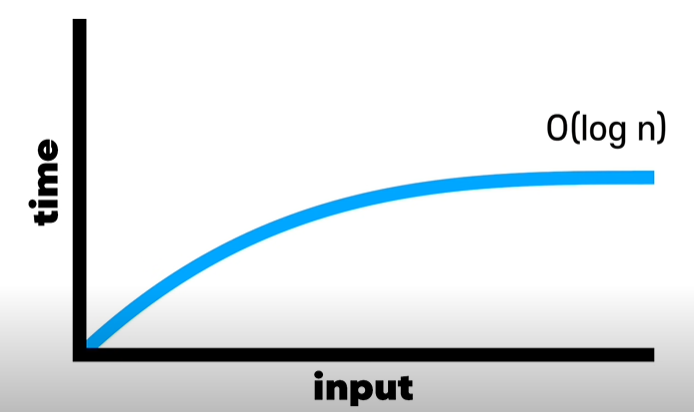
선형시간보다는 빠르고, 상수 시간보다는 느림

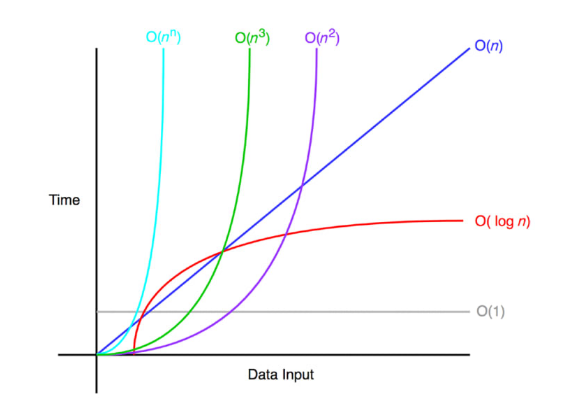
9. O(1) & O(N) & O(logN) 그래프

O(1) > O(logN) > O(N) 순으로 가장 효율적이다.

O(logN)은 아주 조금씩 증가하는 곡선을 그리고 있는데 O(1)보다는 덜 효율적이지만 O(N)보다는 훨씬 효율적이다.

사진 출처 : https://velog.io/@welloff_jj/Complexity-and-Big-O-notation

10. 그렇다면 연습문제

출처 : https://velog.io/@on-n-on-turtle/누구나-자료구조와-알고리즘-빅오표기법

📖 리스트 내 모든 항목을 출력함

public static void printThings() {
    String[] things = {"apples", "chairs", "files", "notes"};

    for (String thing : things)
        System.out.printf("Here's a thing : %s \n", thing);
}

이 알고리즘의 for루프에서 배열의 원소가 4개이기 때문에 4단계가 걸린다.

만약 배열의 원소가 10개이면 10단계가 걸릴 것이다.

for루프에 대입되는 배열의 원소 갯수만큼 단계가 걸리므로 이 알고리즘의 효율성은 O(N)이다.

📖 주어진 해가 윤년인지 알아봄

public static boolean isLeapYear(int year) {
    return (year % 100 == 0) ? (year % 400 == 0) : (year % 4 == 0);
}

N은 number이다.

함수로 전달된 수에 상관없이 단계 수가 일정하므로 O(1)알고리즘이다.

11. 스터디에서 얻은 자주 쓰이는 자료구조의 시간복잡도 정리

8월 23일 국비 강의 들으면서 저번주에 진행한 스터디에서 다른 분이 정리 한 추가 내용

1️⃣ 배열

삽입/삭제: O(N)
탐색: O(1)

👉 파이썬에서는 단순히 List로 구현한다.
👉 탐색할 때 사용하기 좋은 자료구조(삽입이나 삭제는 한자리씩 뒤로 옮기거나 하는 식으로 이루어질 수 있기 때문에, 시간복잡도가 O(N)이된다.)

2️⃣ 벡터 (= 동적배열)

삽입/삭제: O(N)

탐색: O(1)

👉 파이썬에서는 단순히 List로 구현한다.
C++ 같은 언어에서는 배열과 벡터는 다르다.
하지만 파이썬에서는 배열과 같은 List로 쓰면 된다.
List 자체가 이미 동적 배열을 지원해주기 때문이다.

3️⃣ 연결리스트

삽입/삭제: O(1)
탐색: O(N)

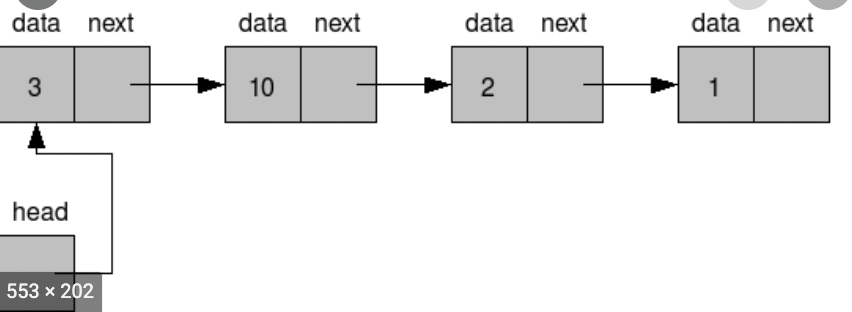
링크드 리스트

👉 시간복잡도 측면에서 배열(List)와 반대 된다. (탐색을 하려면 순간적으로 포인터 부분을 찍고 찍고 가야 하기 때문에 탐색이 O(N)이 되고, 연결 자체의 앞뒤로 수정만 하면 되므로 삽입/삭제시 시간 복잡도가 O(1)이 된다.

👉 링크드 리스트는 백준 문제를 풀며 막 사용할일이 많지는 않지만, 다른 자료구조 구현에도 많이 쓰이니 이론상 알아둘 필요가 있다.

(면접질문으로도 나올 수 있겠다! ex) "우리 프로그램은 삽입/삭제가 빈번한데 어떤 자료구조를 쓸텐가??")

4️⃣ 스택 LIFO

삽입/삭제: O(1)

👉 Last In First Out
👉 파이썬에서 구현은 List로 한다.

s = [1,2,3,4,5,6]

while(len(s)>0):
	print(s[-1])
    s.pop(-1)

위의 코드 처럼 구현 되면 되는데, 배열의 마지막 거를 꺼내는 거다.

5️⃣ 큐 LILO

삽입/삭제: O(1)

👉 줄서기 Last in Last Out
👉 from collections import deque 로 임포트하여 데큐를 사용한다.

from collectionsimport deque

q = deque()
q.append(1)
q.append(2)
q.append(3)

while(len(q) >0):
	print(q.popleft())

위 코드에서 보면 popleft() 라는 함수를 통해 처음에 있는 값을 빼는데, 데큐는 popright()라는 함수도 지원한다.

👉 또한 파이썬에는 Queue도 있고 Deque도 있는데 Queue는 멀티 스레딩도 지원하는 라이브러리여서 Deque보다 느리다. 알고리즘 문제를 푸는 입장이므로 Deque를 사용하는 것이다.

6️⃣ 우선순위큐(내부가 Heap으로 구성)

삽입/삭제 : O(logN)

import heapq

# 리스트를 하나 만들고 사용한다.
pq = []
heapq.heappush(pq,3)
heapq.heappush(pq,1)
heapq.heappush(pq,2)

while(len(pq) >0):
	print(heapq.heappop(pq))

👉 파이썬은 MinHeap 이다.(이진트리의 최상위는 항상 최소값인)

👉 우선 순위 큐 같은 경우에는 , 문제를 풀면서 여러 값들을 넣고 뺄때마다 젤 작은 값이나 젤 큰 값을 알아야 할 때 써야 한다. Sort() 같은 경우 전체 리스트 자체를 정렬해준다는 점에서 큰 차이점을 가진다.

7️⃣ Map(딕셔너리)

삽입/삭제: O(1)

👉 파이썬은 딕셔너리를 사용하면 된다.

추가로, c++같은 경우는 O(logN)이 되는데 이는 c++의 맵은 속을 들여다 보면 이진 그래프로 구현이 되어있기 때문이고, python의 딕셔너리의 경우는 해시로 구현이 되어있기 때문이다.

8️⃣ 집합(set)

삽입/삭제: O(logN)

👉중복을 제거하는게 큰 특징!

12. 빅오의 실행 시간이 짧은 것부터 오래 걸리는 것까지 나열

O(1) - 상수 시간(Constant Time): 입력 크기와 상관없이 항상 일정한 시간이 소요
O(log n) - 로그 시간(Logarithmic Time): 입력의 크기에 대해 로그의 형태로 증가하는 시간이 소요
O(n) - 선형 시간(Linear Time): 입력 크기에 비례하여 시간이 선형으로 증가
O(n log n) - 선형 로그 시간(Linearithmic Time): n과 log n의 곱만큼 시간이 증가
O(n^2) - 이차 시간(Quadratic Time): 입력 크기의 제곱에 비례하여 시간이 증가
O(n^k) - 다항 시간(Polynomial Time): 입력 크기의 k 제곱에 비례하는 시간이 소요(k는 상수).
O(2^n) - 지수 시간(Exponential Time): 입력 크기에 대해 지수적으로 시간이 증가
O(n!) - 팩토리얼 시간(Factorial Time): 입력 크기의 팩토리얼에 비례하는 시간이 소요

GoldenDusk

내 지식을 기록하여, 다른 사람들과 공유하여 함께 발전하는 사람이 되고 싶다. gitbook에도 정리중 ~