자료구조와 알고리즘 공부를 하다 보면 마주치게 되는 복잡도(Complexity)와 빅오 표기법(Big-O notation) ,, 하지만 아무리 백준 문제를 풀어도 나에게 복잡도란 너무 추상적인 개념이었다 🥲
앞으로도 복잡도를 고려해 코딩하는 멋진 개발자가 되고 싶기에 한 번쯤 정리할 필요를 느껴 포스팅해본다.
🧩 복잡도(Complexity)와 마주하기
복잡도란,
- 알고리즘의 성능, 효율성을 나타내는 척도
- 크게 시간 복잡도(Time Complexity)와 공간 복잡도(Space Complexity)로 나눌 수 있다.
- 각 알고리즘이 주어진 특정 크기의 입력(n)을 기준으로 수행시간(연산) 혹은 사용공간이 얼마나 되는지 객관적으로 비교할 수 있는 기준을 제시한다.
- 복잡도를 나타내는 방법으로는 점근 표기법으로 O(빅오), Ω(오메가), Θ(세타) 등이 있고, 주로 빅오와 세타 표기법이 많이 사용된다.
다시 말해, 복잡도라고 말하면 이름 그대로 정말 복잡해 보이지만 그냥 어떤 알고리즘이 효율적인지를 판단하는 척도라고 생각하면 된다!
알고리즘을 평가할 때 주로 수행 시간과 메모리 사용량을 기준으로 두는데, 이 중 수행 시간에 해당하는 것이 시간 복잡도이고 메모리 사용량에 해당하는 것이 공간 복잡도이다.
⏰ 시간 복잡도 (Time Complexity)
시간 복잡도란 특정 크기의 입력을 기준으로 할 때 필요한 연산의 횟수를 나타낸다.
이름은 시간 복잡도이지만 실행 시간이 아닌 연산 횟수를 세는 이유는 다음과 같다.
- 모든 OS, IDE, 플랫폼에서 동일한 결과가 나오지 않는다.
- 실행 시간 측정을 위한 또다른 방법이 필요하다.
💡 더 알아보기: 알고리즘의 성능 평가 Case
- 최선의 경우 (Best Case)
최적의 입력을 한 상태에서, 작업을 완료하는 데 가장 연산 횟수가 적은 경우- 최악의 경우 (Worst Case)
최악의 입력을 한 상태에서, 작업을 완료하는 데 가장 연산 횟수가 많은 경우- 평균의 경우 (Average Case)
여러 경우의 수를 고려하여, 총 연산 횟수를 계산하고 시행 횟수로 나눈 경우
➡️ 알고리즘 분석 시 평균의 경우와 최악의 경우가 가장 많이 활용되며, 알고리즘이 복잡해질수록 평균을 구하기 어려워져 최악의 경우로 알고리즘 성능을 파악한다.
⭐️ 공간 복잡도 (Space Complexity)
공간 복잡도란 프로그램 실행과 완료에 얼마나 많은 공간(메모리)가 필요한지를 나타낸다.
알고리즘을 실행시키기 위해 필요한 공간(space)는 두 가지로 나눌 수 있다.
-
알고리즘과 무관한 공간, 즉 고정 공간
- 코드가 저장되는 공간, 알고리즘 실행을 위해 시스템이 필요로 하는 공간 등
-
알고리즘과 밀접한 공간, 즉 가변 공간
- 문제를 해결하기 위해 알고리즘이 필요로 하는 공간. 변수를 저장하는 공간, 순환 프로그램일 경우 순환 스택(recursion stack) 등
👊🏻 시간 복잡도 vs 공간 복잡도
시간 복잡도는 얼마나 빠르게 실행되는지, 공간 복잡도는 얼마나 많은 자원(메모리 공간)이 필요한지를 판단한다.
시간 복잡도와 공간 복잡도는 반비례하는 경향이 있어, 보통 알고리즘의 성능을 판단할 때는 시간 복잡도를 위주로 판단한다.
🅾️ 빅오 표기법 (Big-O notation)
빅오 표기법(Big-O notation)은 복잡도를 나타내는 점근 표기법 중 가장 많이 사용되는 표기법이다.
빅오 표기법이 가장 많이 사용되는 이유는 알고리즘 효율성을 상한선 기준으로 표기하기 때문이다.
다시 말해 최악의 경우를 고려하는 데 가장 좋은 표기법이다! (알고리즘 효율성은 값이 클수록, 즉 그래프가 위로 향할수록 비효율적임을 의미)
첨언하자면 빅오메가는 하한선을 기준으로, 빅세타는 상한선과 하한선 사이를 기준으로 표기한다.
📈 빅오 표기법의 수학적 정의
빅오 표기법의 수학적 정의는 다음과 같다.
O(g(n)) = {f(n) : there exist positive constants c and $ n_0 $ such that 0≤f(n)≤cg(n) for all n≥$ n_0 $}
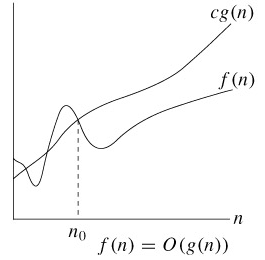
n0를 기준으로 n0보다 오른쪽에 있는 모든 n 값에 대해 함수 f(n)은 함수 cg(n)보다 같거나 작다는 의미이다. - 점근적 상한선
즉 빅오 표기법에서는 주어진 알고리즘이 아무리 나빠도 비교하는 함수와 같거나 좋다!
그래프가 아래에 있을수록 수행시간이 짧으므로 성능이 좋은 것이다.
✏️ 빅오 표기법의 특징
- 상수항 무시
- 빅오 표기법은 n이 충분히 크다고 가정하고 있고, 알고리즘의 효율성은 n의 크기에 영향을 받으므로 상수항 같은 사소한 부분은 무시한다.
➡️ O(2n)은 O(n)으로 간주
- 빅오 표기법은 n이 충분히 크다고 가정하고 있고, 알고리즘의 효율성은 n의 크기에 영향을 받으므로 상수항 같은 사소한 부분은 무시한다.
- 영향력 없는 항 무시
- 빅오 표기법은 n의 크기에 영향을 받으므로 가장 영향력이 큰 항 이외에 영향력이 없는 항은 무시한다.
➡️ O(n^2 + 2n + 1)은 O(n^2)으로 간주
- 빅오 표기법은 n의 크기에 영향을 받으므로 가장 영향력이 큰 항 이외에 영향력이 없는 항은 무시한다.
📕 시간 복잡도와 빅오 표기법
시간 복잡도는 특정 크기의 입력(n)을 기준으로 실행하는 연산의 횟수이다. 다시 말해 연산의 횟수를 세면 된다.
그렇다면 알고리즘이 실행될 때의 모든 연산의 횟수를 세어야 하는가?
답은 아니다. 알고리즘에서 핵심이 되는 연산의 횟수만 세면 된다.
시간 복잡도를 구하는 알고리즘 예제는 여기와 여기에서 한번 보면 이해가 잘 되니 한번쯤 읽어봐야겠다. 물론 내가...
위의 링크에 더해, 빅오 표기법으로 시간 복잡도를 구하는 과정을 잘 정리해주신 글이 있어 가져왔다.
빅오표기법 정리 - with JS
포스팅 하고 나서 풀어봐야겠다.
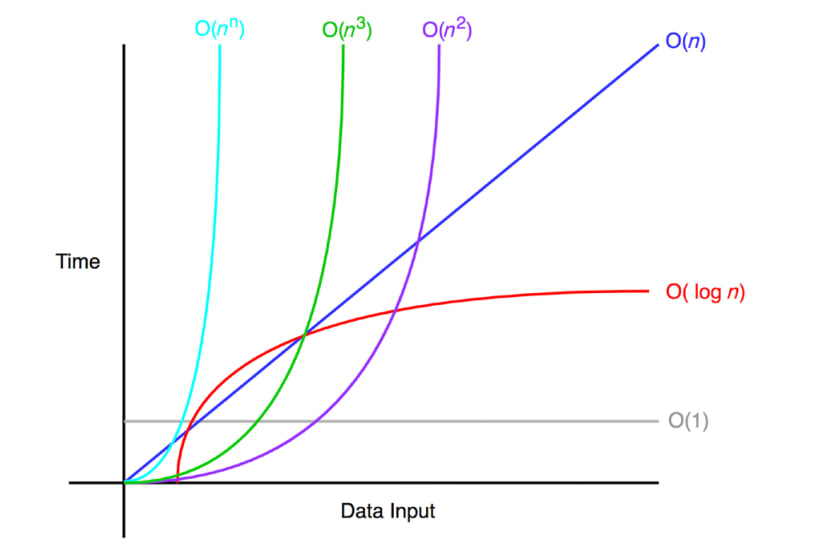
시간 복잡도와 그 예시를 나열해 보면 다음과 같다.
| 복잡도 | 소요 시간 | 예시 |
|---|---|---|
| O(1) | 상수 시간 | 스택에서 Push, Pop |
| O(log n) | 로그 시간 | 이진 트리 |
| O(n) | 직선적 시간 | for 문 |
| O(n log n) | 선형 로그 시간 | 퀵 정렬(quick sort), 병합 정렬(merge sort), 힙 정렬(heap sort) |
| O(n^2) | 2차 시간 | 이중 for 문, 삽입 정렬(insertion sort), 거품 정렬(bubble sort), 선택 정렬(selection sort) |
| O(C^n) | 지수 시간 | 피보나치 수열 |
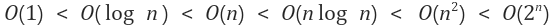
상수함수 < 로그함수 < 선형함수 < 다항함수 < 지수함수
왼쪽에서 오른쪽으로 갈수록 성능이 떨어지며, 시간 복잡도가 좋지 않은 알고리즘이다.
💡 더 알아보기: 시간 복잡도를 구하는 요령
- 하나의 루프를 사용하여 단일 요소 집합을 반복하는 경우: O(n)
- 컬렉션의 절반 이상을 반복하는 경우: O(n / 2) -> O(n)
- 두 개의 다른 루프를 사용하여 두 개의 개별 콜렉션을 반복하는 경우: O(n + m) -> O(n)
- 두 개의 중첩 루프를 사용하여 단일 컬렉션을 반복하는 경우: O(n²)
- 두 개의 중첩 루프를 사용하여 두 개의 다른 콜렉션을 반복하는 경우: O(n * m) -> O(n²)
- 컬렉션 정렬을 사용하는 경우: O(n*log(n))
📗 공간 복잡도와 빅오 표기법
공간 복잡도는 알고리즘 실행에 메모리가 얼마나 사용되는지를 계산하면 된다.
예를 들어 크기가 n인 배열을 입력으로 주었을 때, 알고리즘이 n * n의 이차원 배열을 생성한다면 이 알고리즘의 공간 복잡도는 n^2이다.
알고리즘의 공간 복잡도를 계산한 후 상수항과 영향력 없는 항을 무시해 나타내면 빅오 표기법이 된다. 참 쉽죠? 😜
공간 복잡도는 보통 중요하게 생각하지 않는 경우가 많지만, 많은 데이터를 다루는 경우 공간 복잡도가 커지게 되면 프로그램이 메모리에 올라가지 않아 실행할 수 없게 될 수도 있다.
따라서 알고리즘 작성 시 공간 복잡도도 어느 정도 신경 써서 작성하는 것이 좋다 !!
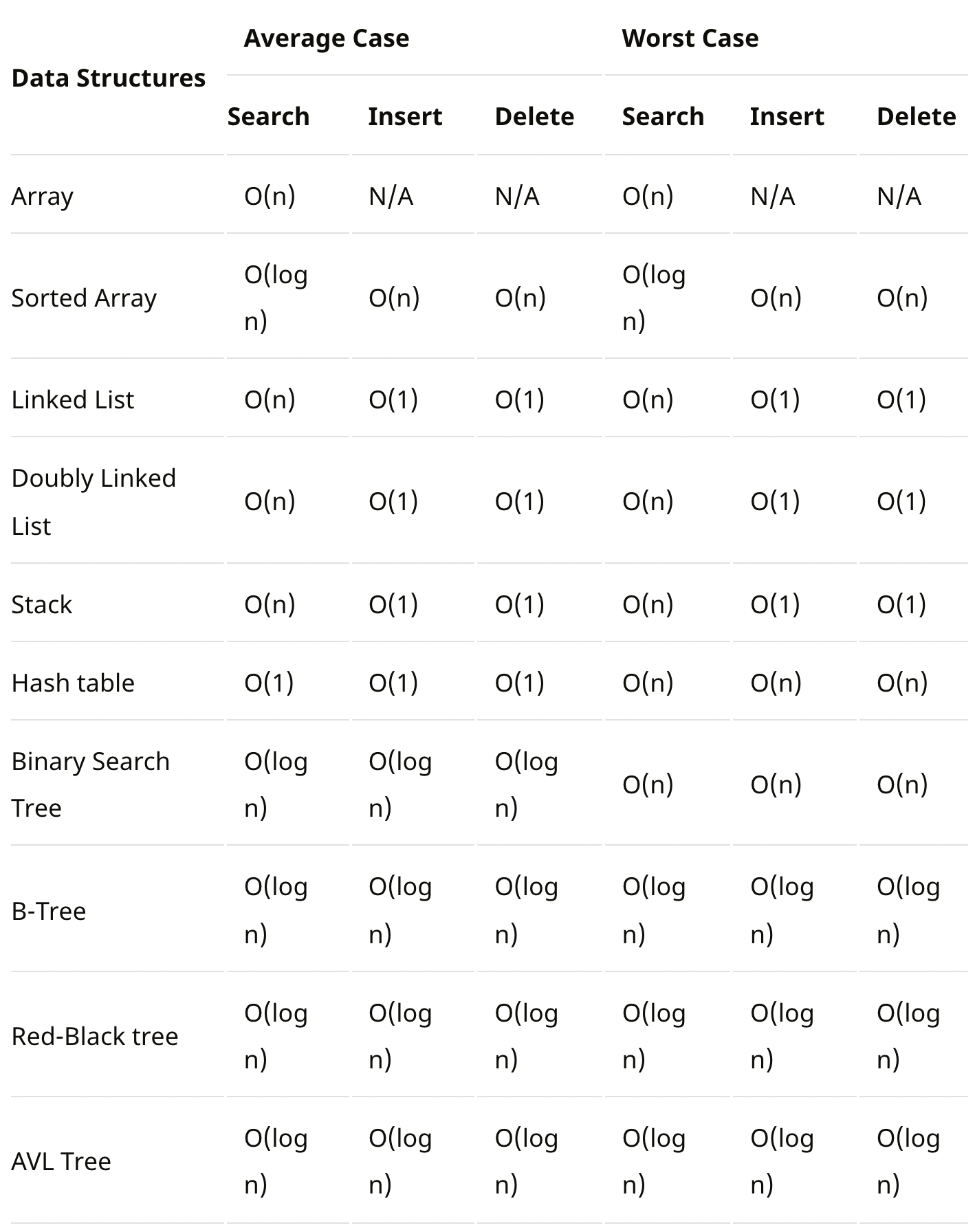
📘 Big-O 표기법으로 나타낸 자료구조별 시간 복잡도
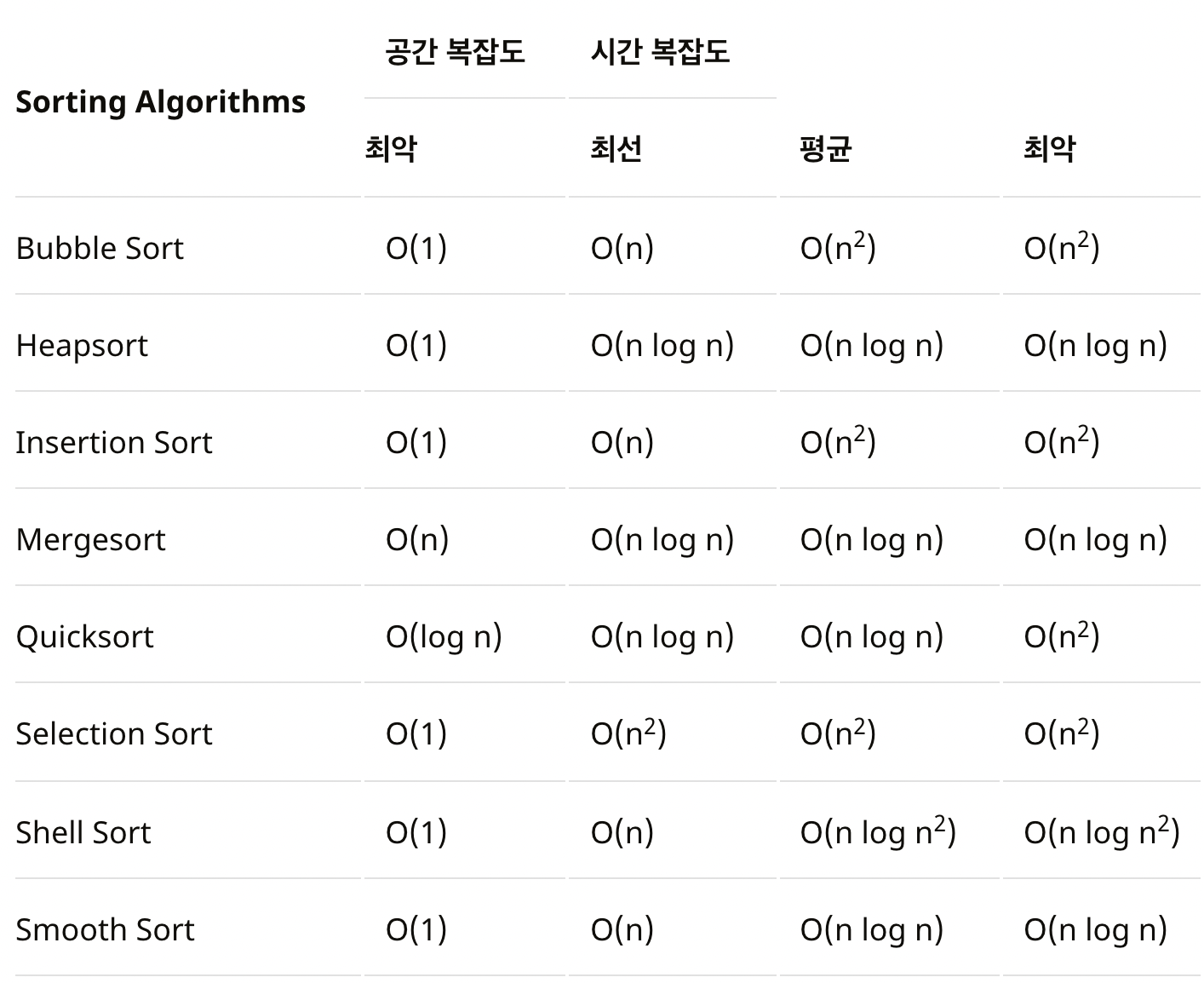
📙 Big-O 표기법으로 나타낸 정렬 알고리즘별 복잡도
참고자료
[컴퓨터 알고리즘 성능분석] 시간 복잡도 vs 공간 복잡도
빅오표기법 정리 - with JS
[Algorithm] 알고리즘 공간복잡도에 대하여
시간 복잡도, 공간 복잡도
알고리즘의 시간 복잡도와 Big-O 쉽게 이해하기
복잡도(Complexity) : 시간 복잡도
빅오 표기법 (big-O notation) 이란


잘 보고 갑니다:) bb