B-Tree 구현법(그림)

B-Tree 구현법(그림)

정렬된 수에 따라 자녀들이 정렬된다.

root: 최상단의 부모값, leaf: 최하단 자녀값
M: 각 노드의 최대 자녀수 → 기준 (자녀수M에 따라 M차 B-Tree라 불리운다.)
M-1: 각 노드의 최대 key 수
M/2(올림): 각 노드의 최소 자녀수 (root, leaf에서 제외)
M/2(올림)-1: 각 노드의 최소 key 수(root에서 제외)

삽입 방법

• 추가는 leaf에서 한다.(끝노드)
• 노드가 넘치면 가운데 key를 기준으로 좌우 key는 분할!하고 가운데 key는 승진한다.

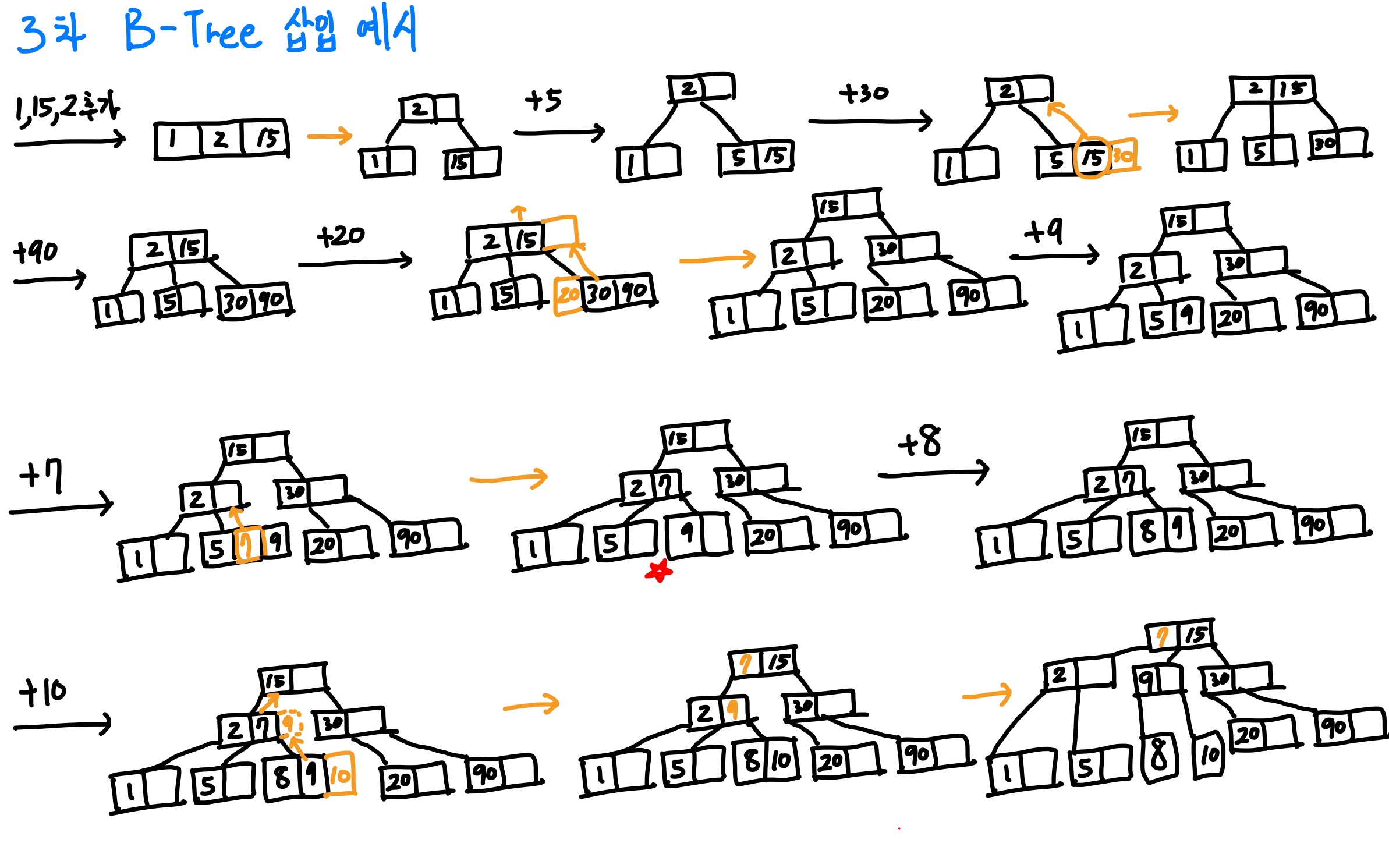
삭제 방법

M/2(올림): 각 노드의 최소 자녀수 (root, leaf에서 제외)
M/2(올림)-1: 각 노드의 최소 key 수(root에서 제외) → 기준으로 정렬
ex) 3차 트리에서 2-1=1로 최소 key 수는 1이다.

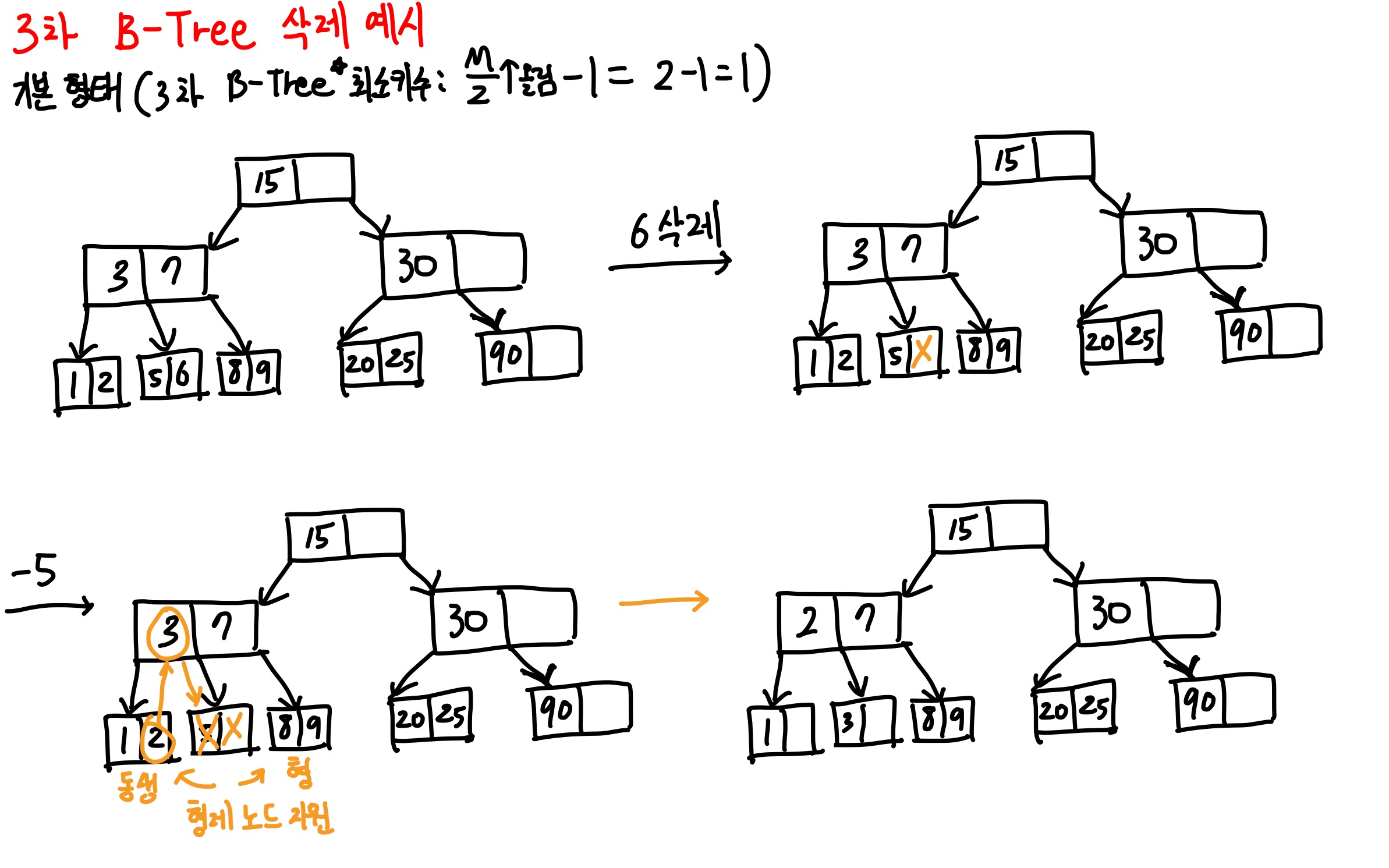
• 삭제는 leaf에서 한다.
• 삭제 후 key 최소 key수 보다 작으면 재조정

→ 재조정 방법
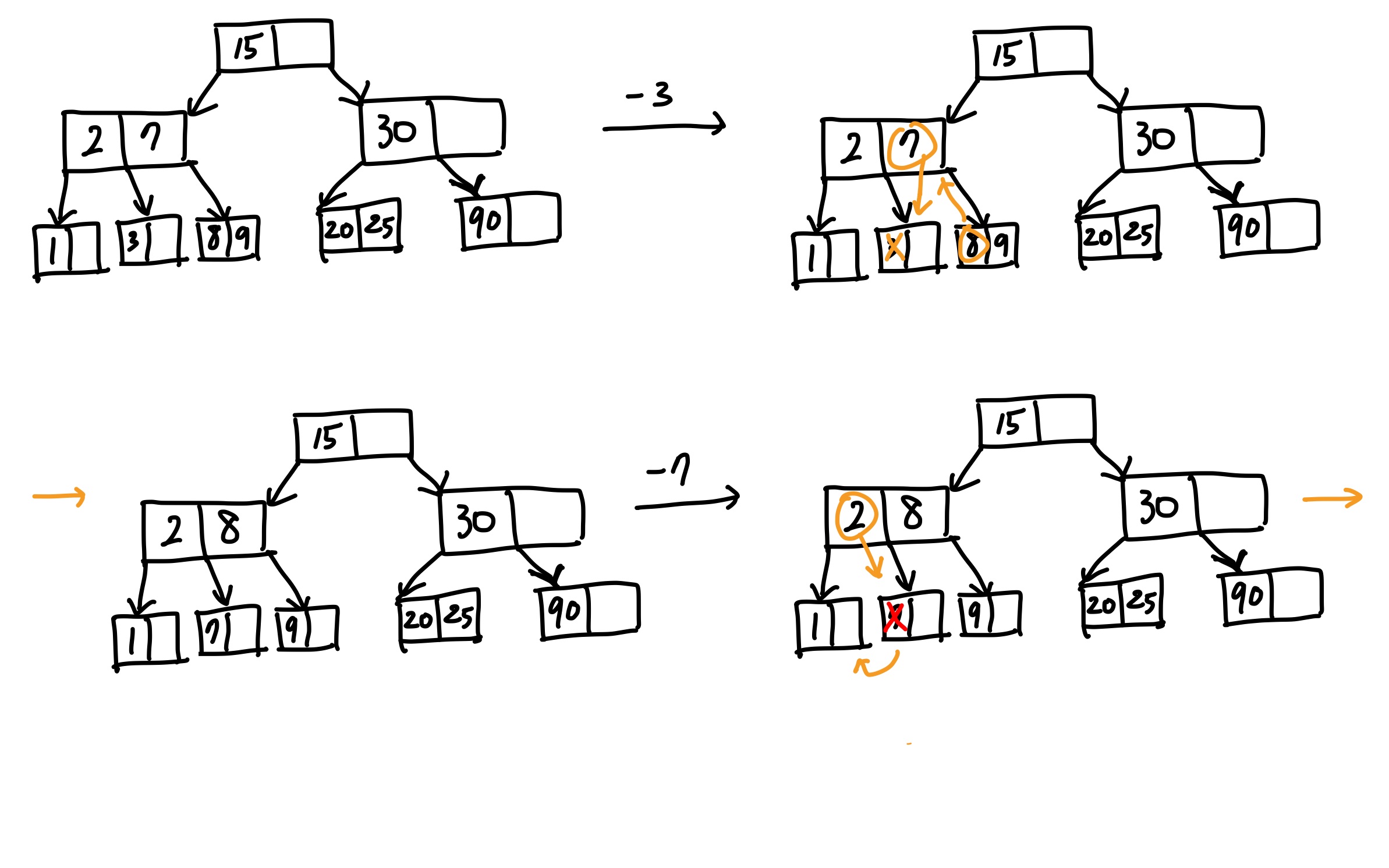
1. key수가 여유있고 인접해있는 형제 노드에게 지원 받는다. (지원시, 부모를 거쳐서 받는다. 그림참조!!)
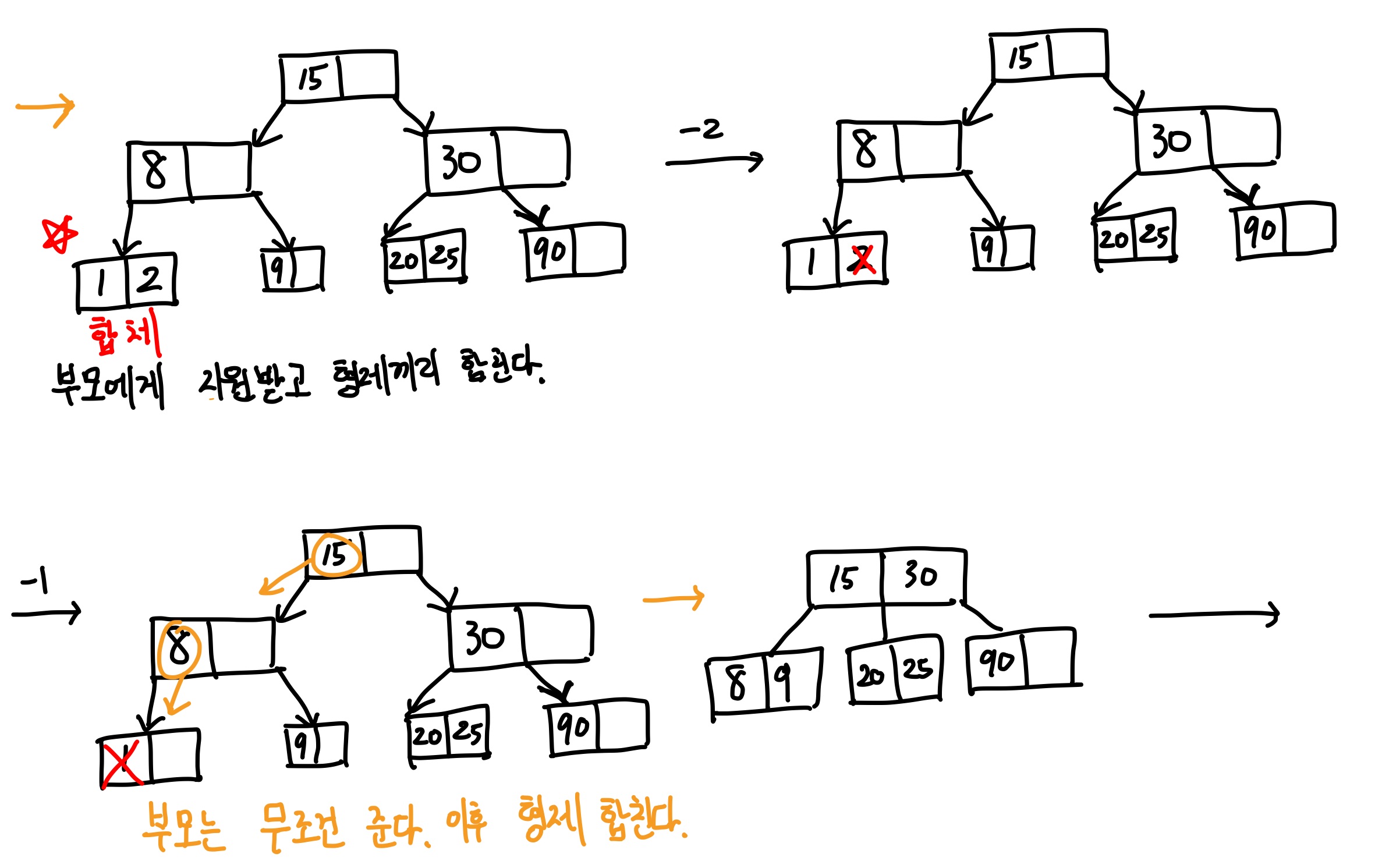
2. 1번 불가 시, 부모에게 지원을 무조건 받고, 형제랑 합친다!
3. 2번 후 부모에게 문제가 생길 시 여기서 위의 내용을 다시 수행하여 재조정한다.

[특이 케이스]iternal 노드 삭제

internal 노드(leaf 노드가 아닌 노드)를 삭제하려면 leaf노드에 있는 데이터랑 위치 바꾸고 삭제.
→ 누구랑 위치를 바꾸는가? 삭제할 데이터의 직전 선임자나 후임자랑 바꿔준다.


왜? internal 노드는 선임자와 후임자랑 바꿀까?

• B-Tree의 균형성을 유지하기 위해.
  (Internal 노드에서 직접 키를 삭제하면 자식 구조가 무너질 수 있으므로, 구조를 덜 흔드는 리프 노드에서 삭제하는 방법을 선택합니다.)
• 선임자/후임자는 항상 B-Tree의 순서를 유지.
  (선임자: 삭제할 키보다 바로 작은 값, 후임자: 삭제할 키보다 바로 큰 값) 이기 때문에, 순서를 깔끔하게 유지할 수 있습니다.
• 재귀적인 삭제 로직의 단순화
  (선임자나 후임자 중 하나로 교체한 후, 그 키를 리프에 가까운 위치로 이동시킴으로써 삭제 로직이 단순해지고 재귀적으로 관리 가능)

→ 트리의 구조를 유지하기 위해서 쓴다. 균형을 유지하기 위해서.

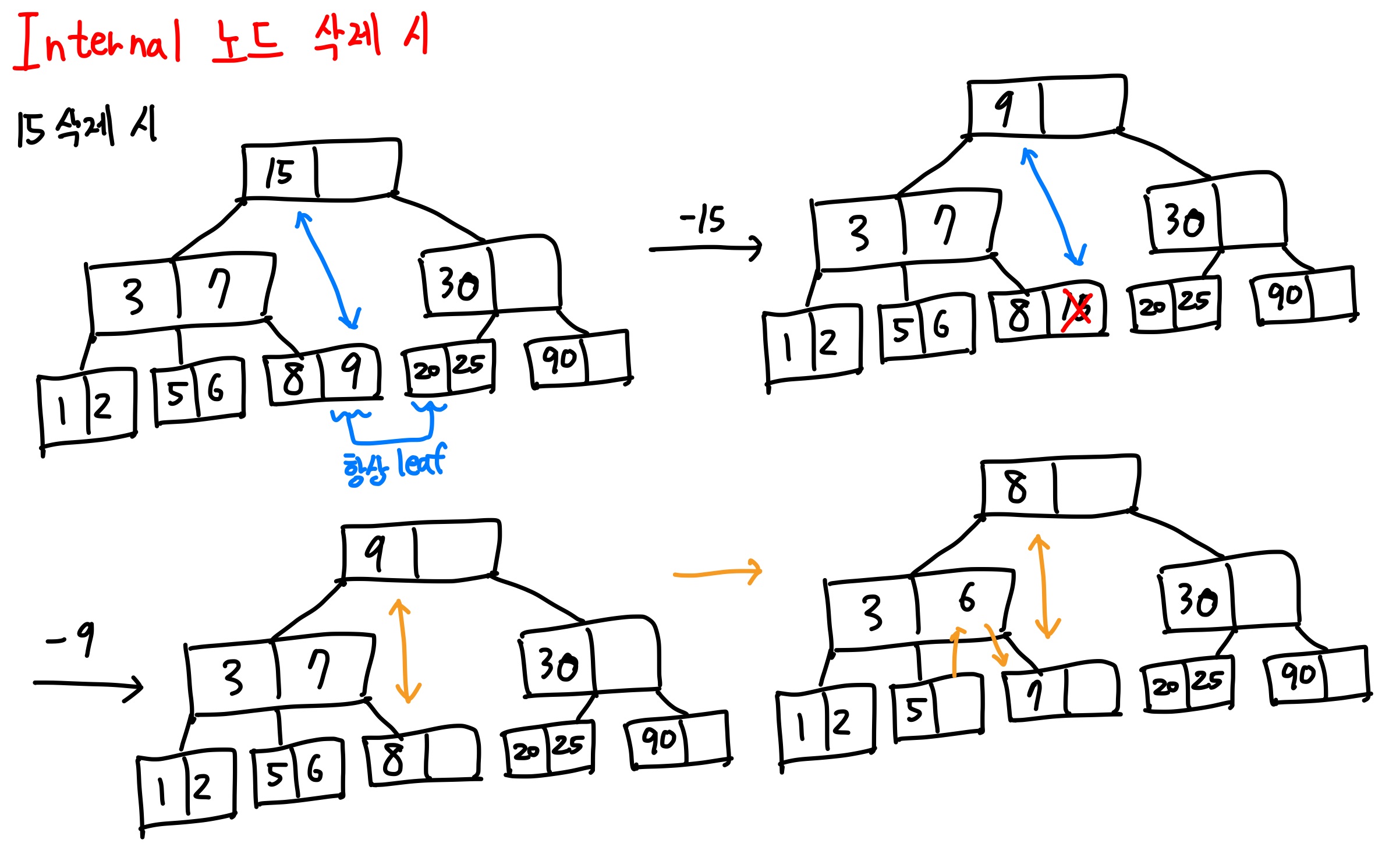
★★★모든 과정에서 적절한 대소 관계인지 확인하고 틀리다면 수정할 것!