B-Tree(C언어 구현 포함)

[참고 사이트]

https://velog.io/@emplam27/%EC%9E%90%EB%A3%8C%EA%B5%AC%EC%A1%B0-%EA%B7%B8%EB%A6%BC%EC%9C%BC%EB%A1%9C-%EC%95%8C%EC%95%84%EB%B3%B4%EB%8A%94-B-Tree

https://yeongjaekong.tistory.com/38

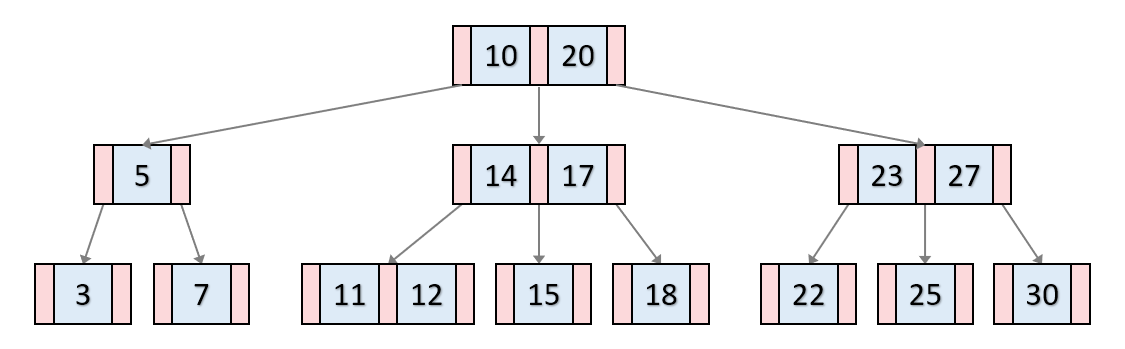
최대 3개의 키와 4개의 자식을 가질수 있는 차수가 3인 B-Tree

B-Tree란?

B-Tree는 이진트리에서 발전되어 모든 리프노드들이 같은 레벨을 가질 수 있도록 자동으로 균형을 맞추는 트리입니다. 정렬된 순서를 보장하고 멀티레벨 인덱싱을 통한 빠른 검색을 할 수 있기 때문에 DB에서 사용하는 자료구조 중 한 종류라고 합니다. B-Tree뿐아니라 B+Tree도 존재합니다.

B트리는 이진트리와 다르게 하나의 노드에 많은 수의 정보를 가지고 있을 수 있습니다. 최대 N개의 자식을 가질 수 있는 B트리를 N차 B트리라고 합니다.

키(key): 각 내부 노드의 키는 하위 트리를 구분하는 구분값 역할

왜 B-Tree는 모든 리프노드들이 같은 레벨이어야할까?
→ 근본적으로 트리의 깊이가 같아야 일관된 검색 속도를 보장할 수 있습니다. 이에 따라 삽입/삭제 시 균형 유지, 디스크 접근 최적화 성능이 안정적으로 유지되기 때문입니다.

특징

• 노드는 최대 M개 부터 M/2개 까지의 자식을 가질 수 있습니다.
• 모든 리프 노드는 같은 깊이에 있습니다.
• 각 노드는 일정 범위의 키를 저장합니다.(키는 노드 내에 정렬)
• 노드에는 최대 M−1개 부터 (M/2)−1개의 키가 포함될 수 있습니다.
• 노드의 키가 x개라면 자식의 수는 x+1개 입니다.
• 최소차수는 자식수의 하한값을 의미하며, 최소차수가 t라면 M=2t−1을 만족합니다. (최소차수 t가 2라면 3차 B트리이며, key의 하한은 1개입니다.)
• 탐색, 삽입, 삭제 모두 가능한 트리입니다.

→ 이러한 특징으로 B-Tree는 디스크 접근을 최소화하기 위해 설계되었고, 대용량 데이터 저장에 효율적입니다.

GIF 추가

[중요!] Big O 데이터 시간 복잡도에 대해서

보통 DB에서 자주 사용하는 트리입니다. 큰 양의 정렬된 데이터를 관리하는 DB특성상 B-Tree를 사용하면 데이터 검색 성능이 향상될 수 있습니다. B-Tree인덱스를 사용할 때와 사용하지 않을 때(Tree 등) 데이터 검색 시간 복잡도를 Big O 표기법을 활용하여 비교하고 설명해보겠습니다.

→ B-Tree 인덱스를 사용할 때의 데이터 검색 시간 복잡도는 O(logN)이다. 여기서 N은 DB 내의 레코드 수입니다. B-Tree 구조는 균형 이진 트리와 유사하므로 데이터를 효율적으로 검색할 수 있습니다.
반면, B-Tree 인덱스를 사용하지 않을 경우 선형 검색을 수행하므로 검색시간 복잡도는 O(N)이 됩니다. (모든 데이터 확인) 따라서, 데이터 양이 많을수록 B-Tree인덱스를 사용하는 것이 성능 면에서 훨씬 유리합니다.

B-Tree 구조

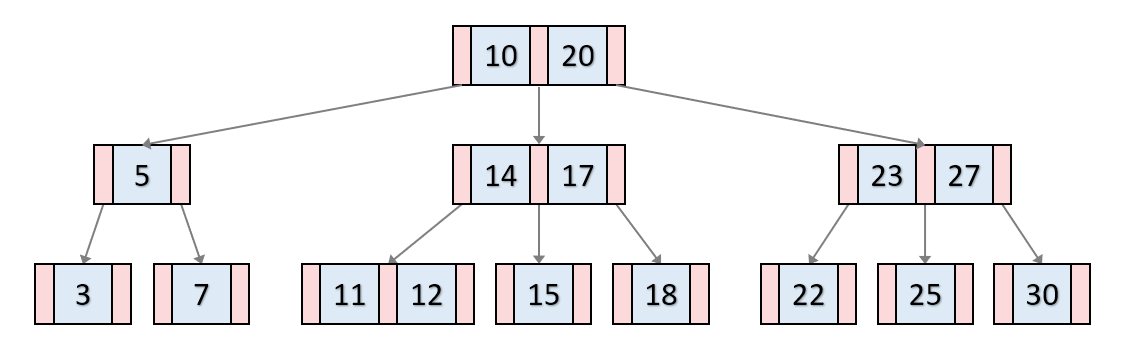
위 B-Tree는 차수가 3(M)입니다. 한 노드당 키는 2개(M-1)까지 가능!
파란색 부분: 각 노드의 키를 나타낸다. [키(key): 각 내부 노드의 키는 하위 트리를 구분하는 구분값 역할]
빨간색 부분: 자식 노드들을 가르키는 포인터 입니다.

→ 키(key) 특징
노드안에서 항상 정렬된 값을 가진다.
이진검색 트리처럼 각 key들의 왼쪽 자식들은 항상 key보다 작은 값을 / 오른쪽 자식은 큰 값을 가집니다.

구조체 정의 부분

#define MAX_KEYS 3  // 3차 B-트리 예시 (최대 3개의 키)
#define MIN_KEYS 1  // 최소 키 개수 (MAX_KEYS/2 내림)

typedef struct BTreeNode {
    int keys[MAX_KEYS];           // 키 배열
    struct BTreeNode* children[MAX_KEYS + 1];  // 자식 포인터 배열
    int keyCount;                 // 현재 노드에 저장된 키의 개수
    bool leaf;                    // 리프 노드 여부
} BTreeNode;

typedef struct BTree {
    BTreeNode* root;              // 루트 노드 포인터
    int t;                        // 최소 차수
} BTree;

초기화 함수

BTreeNode* createNode(bool leaf) {
    BTreeNode* newNode = (BTreeNode*)malloc(sizeof(BTreeNode));
    if (newNode) {
        newNode->leaf = leaf;
        newNode->keyCount = 0;
        for (int i = 0; i < MAX_KEYS + 1; i++) {
            newNode->children[i] = NULL;
        }
    }
    return newNode;
}

BTree* createBTree() {
    BTree* tree = (BTree*)malloc(sizeof(BTree));
    if (tree) {
        tree->root = createNode(true);
        tree->t = (MAX_KEYS + 1) / 2;  // 최소 차수 설정
    }
    return tree;
}

---

키 검색과정

루트노드에서 시작해서 하향식으로 검색을 수행합니다. 검색하고자 하는 key를 k이라고 하였을 때 검색 과정입니다.

1. 루트 노드에서 시작하여 key들을 순회하며 검사.
   → 만약, k와 같은 key를 찾으면 검색 종료.
   → 검색하는 값과 key들의 대소관계를 비교하여 어떤 key들 사이 k가 들어가면 해당 key들 사이의 자식 노드로 내려감(빨간색 포인터)
2. 해당 과정을 리프 노드에 도달할 때까지 반복합니다. 만일 리프노드에도 k와 같은 key가 없다면 검색을 실패합니다.

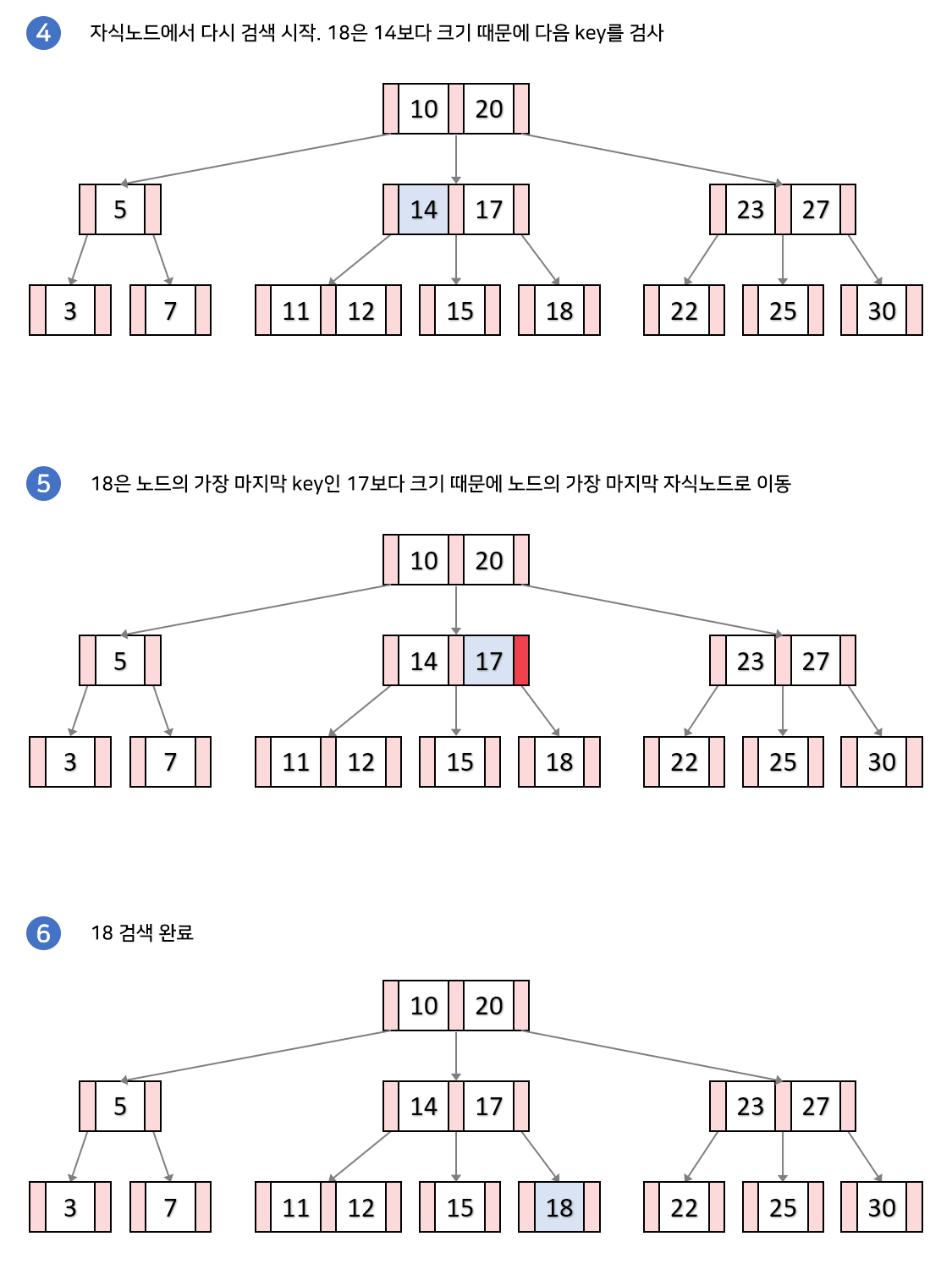
밑의 그림은 18을 키 검색하는 과정입니다.

검색 함수 코드

// 노드 내에서 주어진 키를 검색
int findKey(BTreeNode* node, int key) {
    int idx = 0;
    while (idx < node->keyCount && node->keys[idx] < key)
        idx++;
    return idx;
}

// B-트리에서 키 검색
BTreeNode* search(BTreeNode* root, int key) {
    int i = findKey(root, key);
    
    // 키를 찾았다면 현재 노드 반환
    if (i < root->keyCount && root->keys[i] == key)
        return root;
    
    // 리프 노드인데 키를 찾지 못했다면 NULL 반환
    if (root->leaf)
        return NULL;
    
    // 적절한 자식 노드로 재귀 호출
    return search(root->children[i], key);
}

---

키 삽입과정

key를 삽입하기 위해서는 다음과 같은 과정이 필요합니다.
→ 요소 삽입에 적절한 리프 노드를 검색, 필요한 경우 노드를 분할

리프노드 검색은 하향식이지만 노드 분할의 과정은 상향식으로 이루어진다고 볼 수 있습니다. 다음은 삽입하고자 하는 값을 k로 하였을 때 삽입 과정입니다.

1. 트리가 비어있으면 루트 노드를 할당하고 k를 삽입합니다. 만일 루트노드가 가득 찼다면, 노드를 분할하고 리프노드가 생성됩니다.
2. 이후부터는 삽압하기에 적절한 리프노드를 찾아 k를 삽입합니다. 삽입위치는 노드의 key값과 k값을 검색 연산과 동일한 방법으로 비교하면서 찾습니다.

이후 두가지 케이스로 나뉘게 됩니다.

상황1. 분할이 일어나지 않은 경우

리프 노드가 가득차지 않았으면, 오름차순으로 k를 삽입합니다.

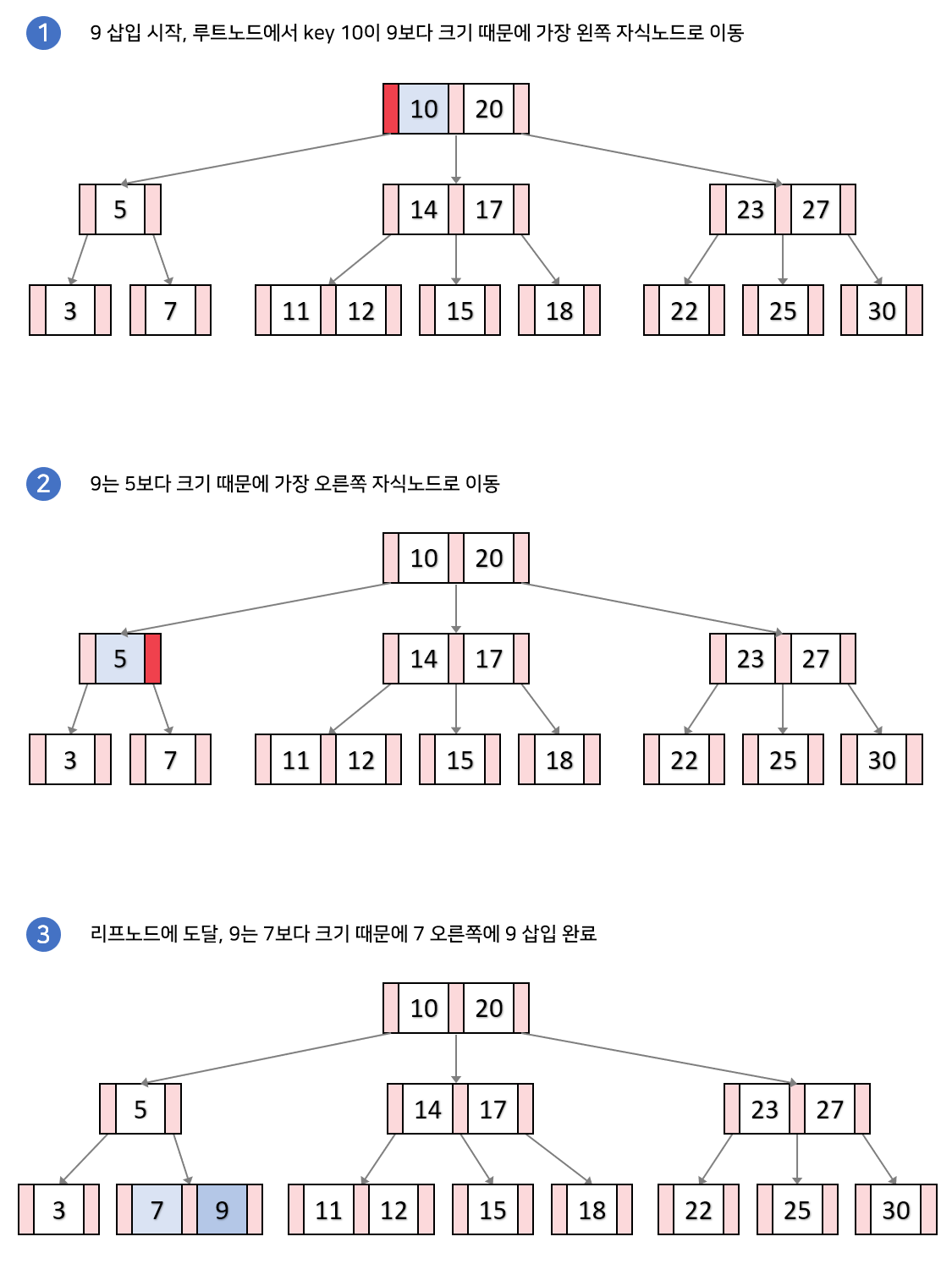
밑에 그림은 9를 삽입하는 과정입니다.

상황2. 분할이 일어나는 경우

만일 리프노드에 key노드가 가득 찬 경우, 노드를 분할해야 합니다.

1. 오름차순으로 요소를 삽입할때, 마지막 노드가 담을 수 있는 최대 key 개수(2개)를 초과하게 됩니다.
2. 중앙값으로 분할을 수행합니다. 중앙값은 부모 노드로 병합하거나 새로 생성됩니다.(위로 올림)
   왼쪽 키들은 왼쪽 자식으로, 오른쪽 키들은 오른쪽 자식으로 분할됩니다.
3. 부모 노드를 검사해서 또 다시 가득 찼다면, 다시 부모노드에서 위 과정을 반복합니다.
   (해당 차수가 3이므로 각 노드 당 키 최대 2개, 차수가 4이면 키 3개까지 가능)

밑에는 13을 삽입하는 과정입니다.

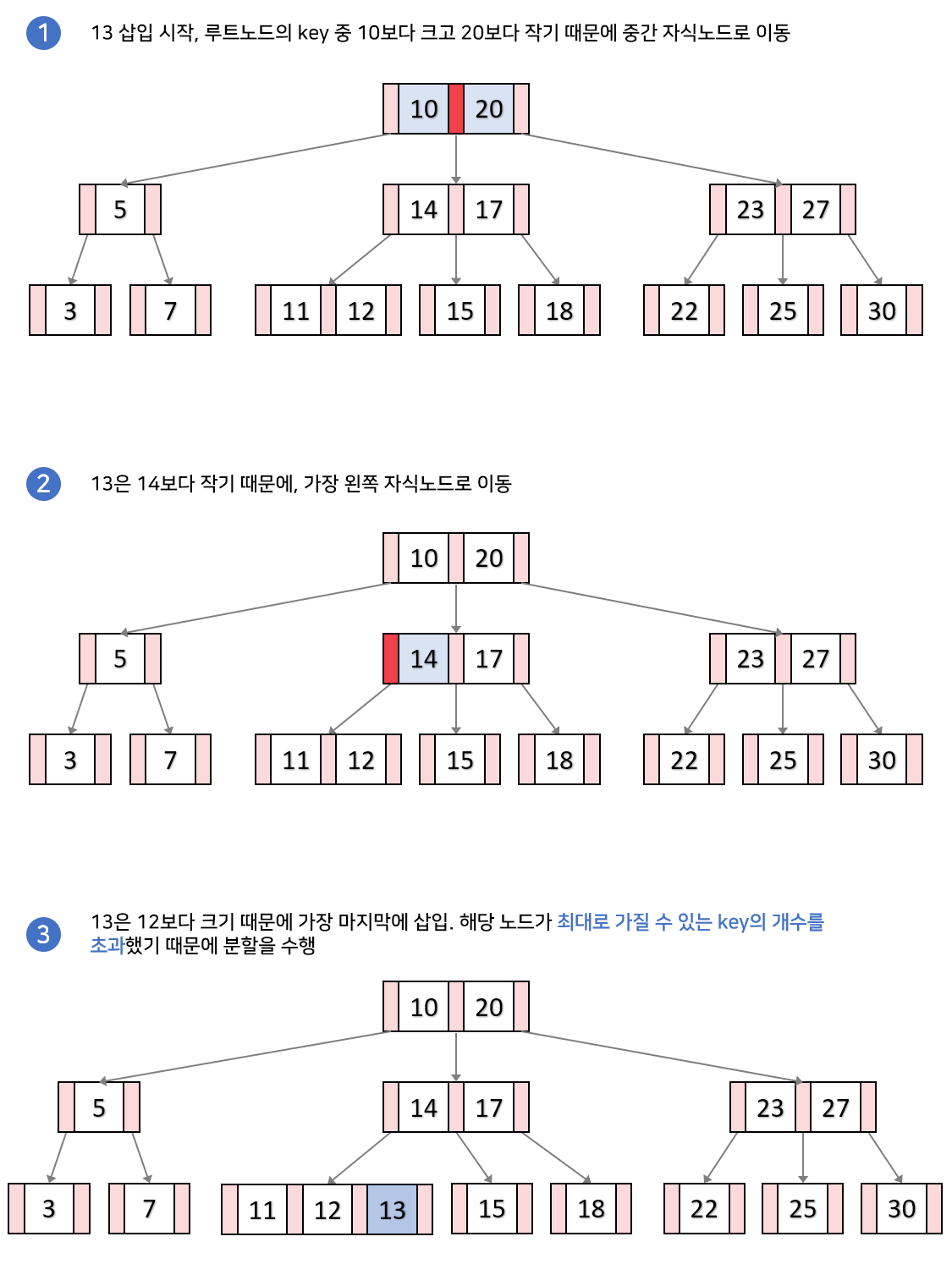
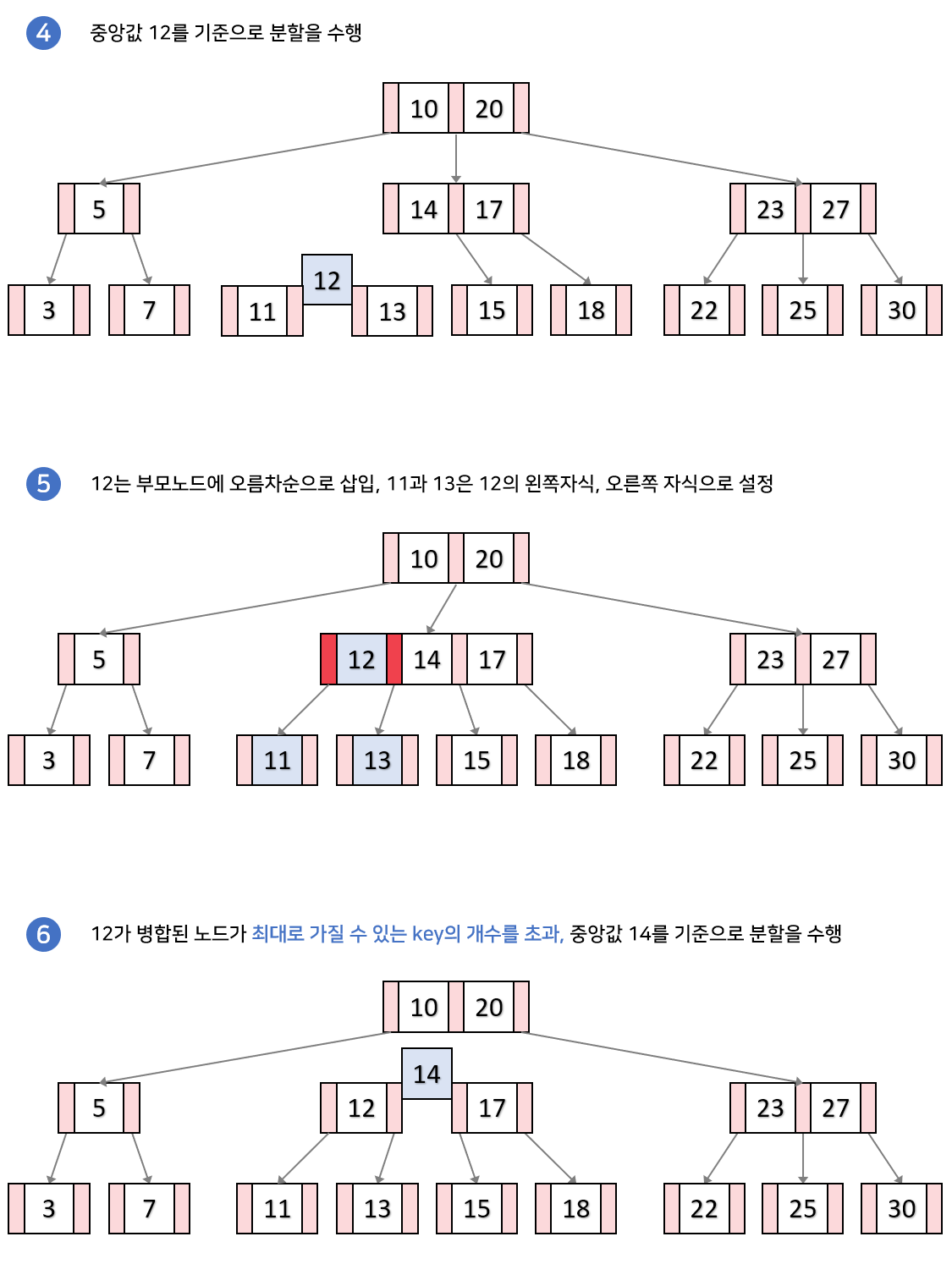
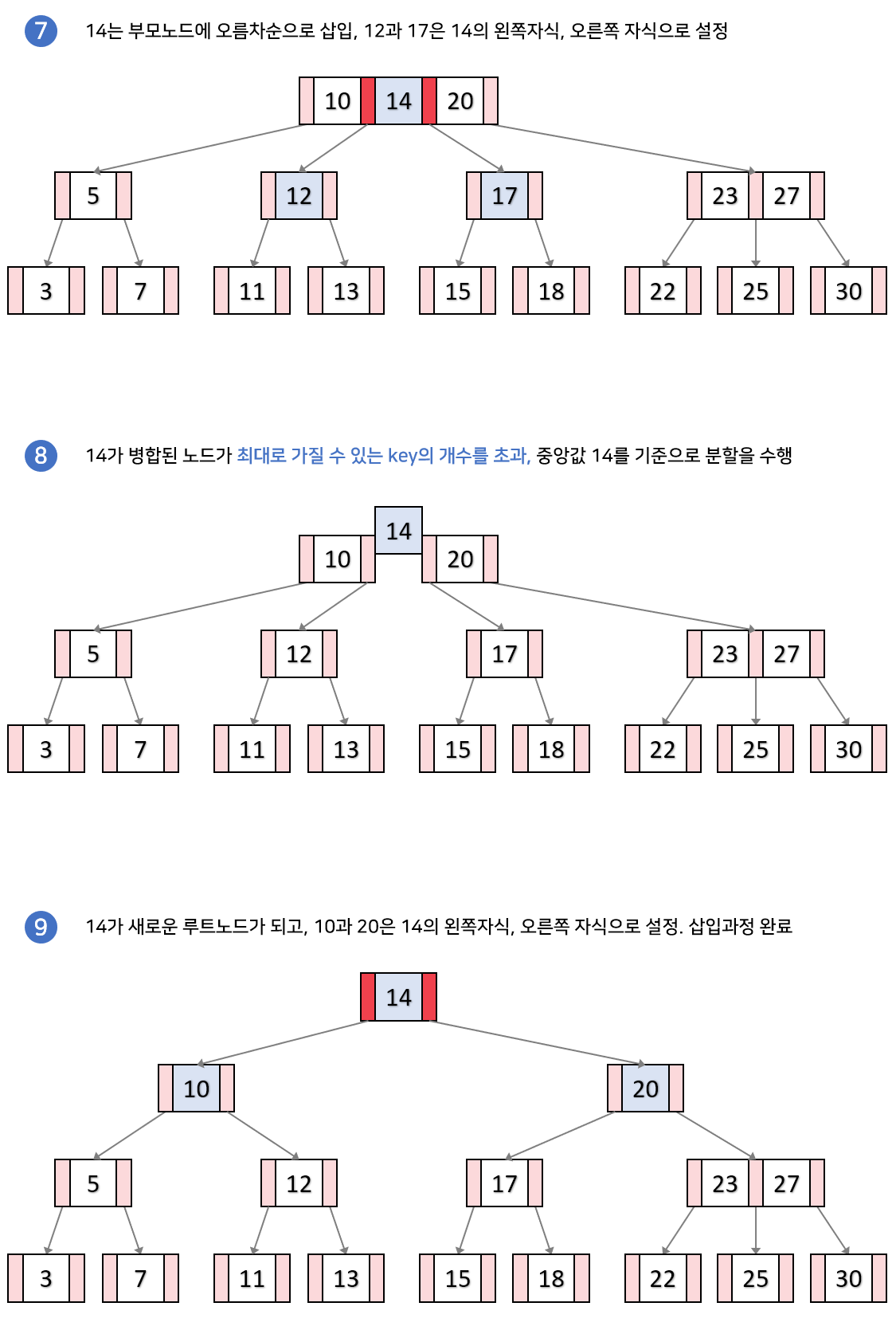
삽입 함수

// 노드 분할 함수 (노드가 가득 찼을 때 호출)
void splitChild(BTreeNode* parent, int index, BTreeNode* child) {
    BTreeNode* newNode = createNode(child->leaf);
    newNode->keyCount = MIN_KEYS;
    
    // 새 노드로 키 복사 (중간 이후)
    for (int j = 0; j < MIN_KEYS; j++) {
        newNode->keys[j] = child->keys[j + MIN_KEYS + 1];
    }
    
    // 리프 노드가 아니면 자식 포인터도 복사
    if (!child->leaf) {
        for (int j = 0; j <= MIN_KEYS; j++) {
            newNode->children[j] = child->children[j + MIN_KEYS + 1];
        }
    }
    
    // 원래 노드의 키 개수 조정
    child->keyCount = MIN_KEYS;
    
    // 부모 노드에 공간 확보
    for (int j = parent->keyCount; j > index; j--) {
        parent->children[j + 1] = parent->children[j];
    }
    
    // 새 노드를 부모의 자식으로 연결
    parent->children[index + 1] = newNode;
    
    // 부모 노드에 키 이동
    for (int j = parent->keyCount - 1; j >= index; j--) {
        parent->keys[j + 1] = parent->keys[j];
    }
    
    // 중앙 키를 부모로 이동
    parent->keys[index] = child->keys[MIN_KEYS];
    parent->keyCount++;
}

// 노드에 키 삽입 (노드가 가득 차지 않았다고 가정)
void insertNonFull(BTreeNode* node, int key) {
    int i = node->keyCount - 1;
    
    if (node->leaf) {
        // 리프 노드면 키를 적절한 위치에 삽입
        while (i >= 0 && key < node->keys[i]) {
            node->keys[i + 1] = node->keys[i];
            i--;
        }
        node->keys[i + 1] = key;
        node->keyCount++;
    } else {
        // 내부 노드면 적절한 자식을 찾아 재귀 호출
        while (i >= 0 && key < node->keys[i])
            i--;
        i++;
        
        // 자식 노드가 가득 찼는지 확인
        if (node->children[i]->keyCount == MAX_KEYS) {
            splitChild(node, i, node->children[i]);
            if (key > node->keys[i])
                i++;
        }
        insertNonFull(node->children[i], key);
    }
}

// B-트리에 키 삽입
void insert(BTree* tree, int key) {
    BTreeNode* root = tree->root;
    
    // 루트가 가득 찼는지 확인
    if (root->keyCount == MAX_KEYS) {
        BTreeNode* newRoot = createNode(false);
        newRoot->children[0] = root;
        tree->root = newRoot;
        splitChild(newRoot, 0, root);
        insertNonFull(newRoot, key);
    } else {
        insertNonFull(root, key);
    }
}

---

키 삭제 과정

요소 삭제를 위한 조건

1. 삭제할 키가 있는 노드 검색
2. 키 삭제
3. 필요에 따라 트리 균형 조정

삭제를 위해선 몇가지 용어를 아는 것이 좋습니다.

• inorder predecessor : 노드의 왼쪽 자손에서 가장 큰 key
• inorder successor : 노드의 오른쪽 자손에서 가장 작은 key
• 부모key: 부모 노드의 key들 중 왼쪽 자식으로 본인 노드를 가지고 있는 key값입니다.
  (단, 마지막 자식 노드의 경우에는 부모의 마지막 key입니다.)

상황1. 삭제할 키 k가 리프에 있는 경우

상황1-1. 현재 노드의 key 개수가 최소 key 개수보다 크다면?

다른 노드들에 영향 없이 k를 단순 삭제

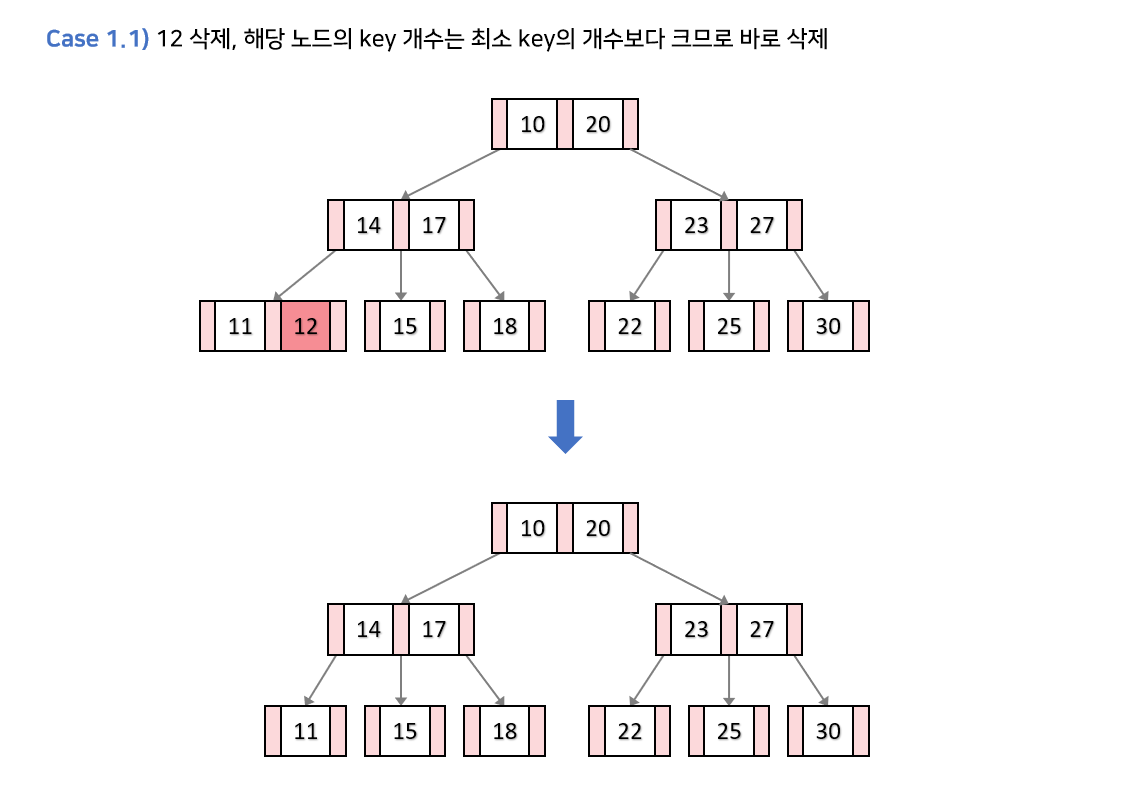
상황1-2. 왼쪽 or 오른쪽 형제 노드의 key가 최소 key 개수 이상이라면?

1. 부모 key 값으로 k를 대체합니다.
2. 최소키 개수 이상의 키를 가진 형제 노드가
   왼쪽 형제라면 형제 노드의 가장 큰 값을 부모 key로 올리고, 부모 key는 자식 노드로 내려간다.
   오른쪽 형제라면 형제 노드의 가장 작은 값을 부모 key로 올리고, 부모 key는 자식 노드로 내려간다.

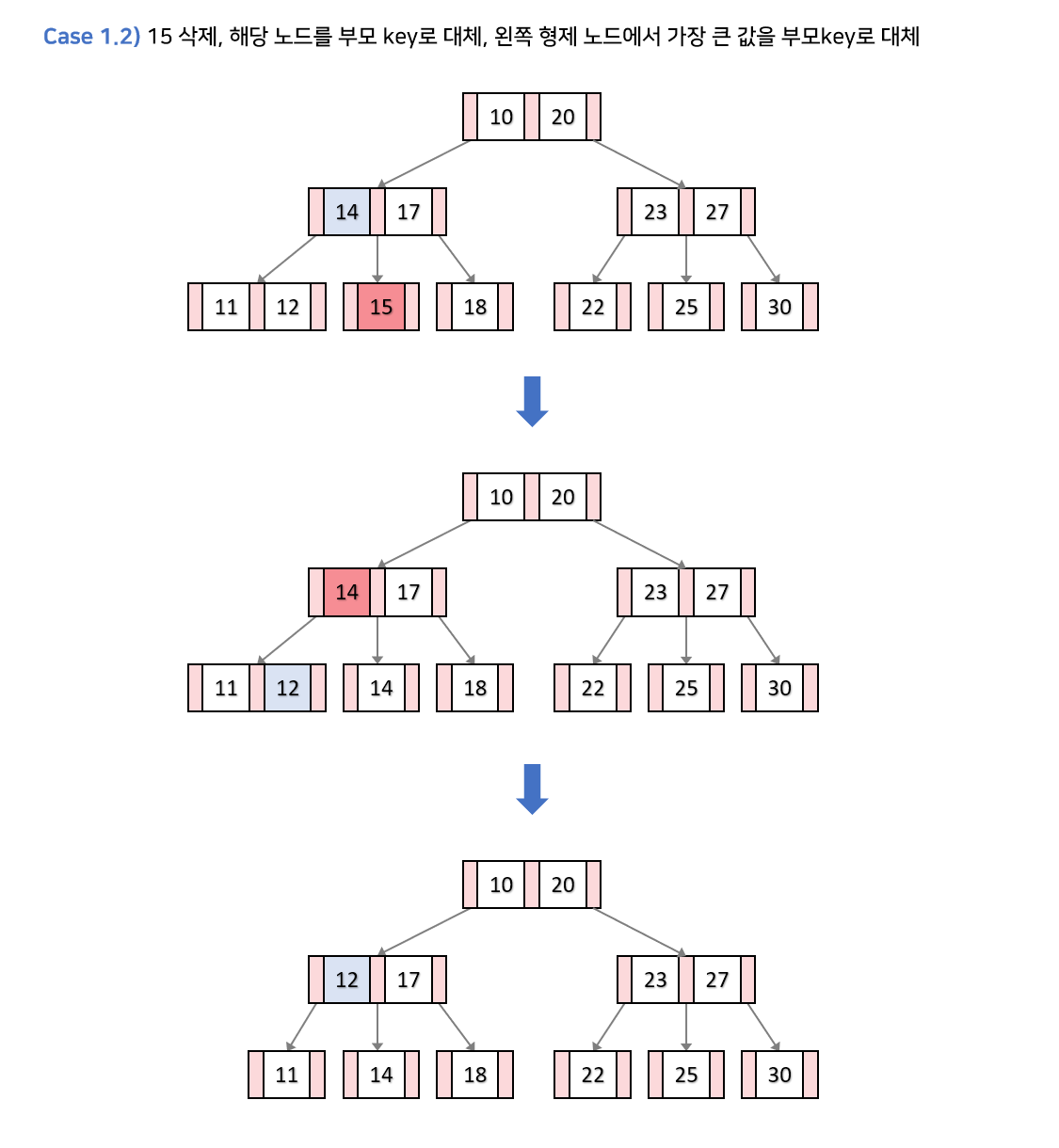
상황1-3. 왼쪽, 오른쪽 형제 노드의 key가 최소 key 개수이고, 부모노드의 key가 최소개수 이상이면

1. k를 삭제한 후, 부모key를 형제 노드와 병합합니다.
2. 부모노드의 key개수를 하나 줄이고, 자식 수 역시 하나를 줄여 B-Tree를 유지합니다.

상황1-4. 자신과 형제, 부모 노드의 key 개수가 모두 최소 key 개수라면

부모노드를 루트노드로 한 부분 트리의 높이가 줄어드는 경우이기 때문에 재구조화의 과정이 일어납니다.
상황3의 2번 과정으로 이동합니다.

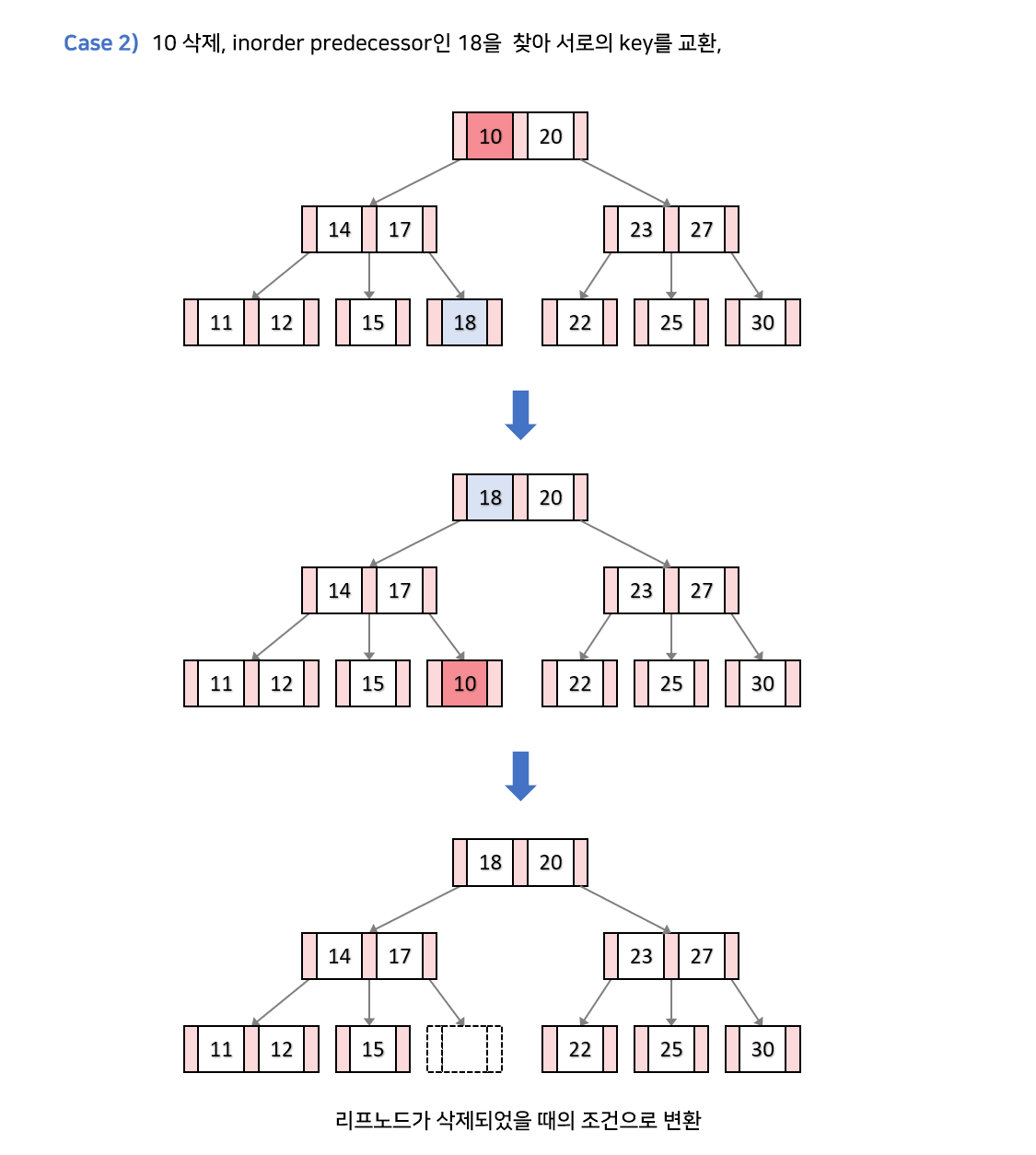
상황2. 삭제할 key k가 내부 노드에 있고, 노드나 자식에 키가 최소 키수보다 많을 경우

1. 현재 노드의 inorder predecessor 또는 inorder successor와 k의 자리를 바꿉니다.
2. 리프노드의 k를 삭제하게 되면, 리프노드가 삭제 되었을 때의 조건으로 변합니다.
   삭제한 리프노드에 대해서 상황 1 조건으로 이동합니다.

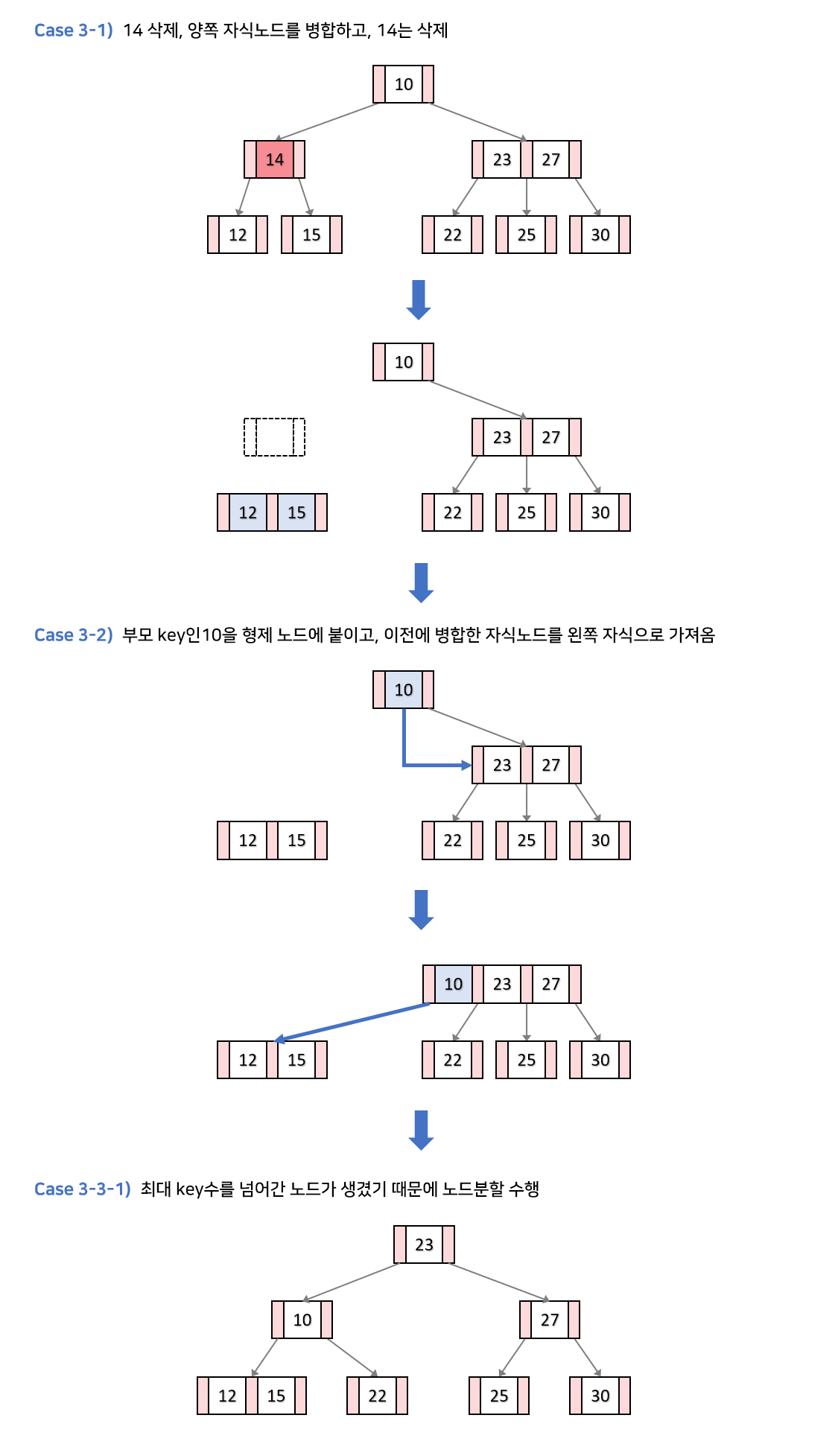
상황3. 삭제할 key k가 내부 노드에 있고, 노드에 key 개수가 최소key 개수만큼, 노드의 자식 key 개수도 모두 최소 key 개수인 경우

삭제할 key k가 있는 노드도 최소, 자식노드들도 최소의 key 개수를 가지므로, k를 삭제하면 트리의 높이가 줄어들어 재구조화가 일어나는 케이스입니다.
재구조화의 과정은 다음과 같습니다.

1. k를 삭제하고, k의 양쪽 자식을 병합하여 하나의 노드로 만듭니다.
2. k의 부모key를 인접한 형제 노드에 붙입니다. 이후, 이전에 병합했던 노드를 자식노드로 설정합니다.
3. 해당 과정을 수행하였을 때 부모노드의 개수가 에 따라 이후 수행 과정이 달라집니다.
   3-1. 만일 새로 구성된 인접 형제노드의 key가 최대 key 개수를 넘어갔다면, 삽입 연산의 노드 분할 과정을 수행합니다.
   3-2. 만일 인접 형제노드가 새로 구성되더라도 원래 k의 부모 노드가 최소 key의 개수보다 작아진다면, 부모 노드에 대하여 2번 과정부터 다시 수행합니다.

상황 3-3-2. 새로운 트리에서의 예시

void removeFromNode(BTreeNode* node, int k);

void removeFromLeaf(BTreeNode* node, int idx) {
    // 리프 노드에서 단순히 제거
    for (int i = idx + 1; i < node->n; ++i)
        node->keys[i - 1] = node->keys[i];
    node->n--;
}

void removeFromNonLeaf(BTreeNode* node, int idx) {
    int k = node->keys[idx];
    
    BTreeNode* leftChild = node->children[idx];
    BTreeNode* rightChild = node->children[idx + 1];

    // Case 1: 왼쪽 자식에서 전임자(pred)를 가져와 대체
    if (leftChild->n >= T) {
        int pred = getPredecessor(leftChild);
        node->keys[idx] = pred;
        removeFromNode(leftChild, pred);
    }
    // Case 2: 오른쪽 자식에서 후임자(succ)를 가져와 대체
    else if (rightChild->n >= T) {
        int succ = getSuccessor(rightChild);
        node->keys[idx] = succ;
        removeFromNode(rightChild, succ);
    }
    // Case 3: 양쪽 자식 모두 최소 키 개수 → 병합 후 재귀 삭제
    else {
        merge(node, idx);
        removeFromNode(leftChild, k);
    }
}

int getPredecessor(BTreeNode* node) {
    while (!node->leaf)
        node = node->children[node->n];
    return node->keys[node->n - 1];
}

int getSuccessor(BTreeNode* node) {
    while (!node->leaf)
        node = node->children[0];
    return node->keys[0];
}

void merge(BTreeNode* node, int idx) {
    BTreeNode* left = node->children[idx];
    BTreeNode* right = node->children[idx + 1];

    left->keys[T - 1] = node->keys[idx];

    for (int i = 0; i < right->n; ++i)
        left->keys[i + T] = right->keys[i];

    if (!left->leaf) {
        for (int i = 0; i <= right->n; ++i)
            left->children[i + T] = right->children[i];
    }

    for (int i = idx + 1; i < node->n; ++i)
        node->keys[i - 1] = node->keys[i];
    for (int i = idx + 2; i <= node->n; ++i)
        node->children[i - 1] = node->children[i];

    left->n += right->n + 1;
    node->n--;

    free(right);
}

void removeFromNode(BTreeNode* node, int k) {
    int idx = 0;
    while (idx < node->n && node->keys[idx] < k)
        idx++;

    // Case 1: 키가 현재 노드에 존재하는 경우
    if (idx < node->n && node->keys[idx] == k) {
        if (node->leaf)
            removeFromLeaf(node, idx);
        else
            removeFromNonLeaf(node, idx);
    }
    // Case 2: 키가 자식 노드에 존재
    else {
        if (node->leaf) {
            printf("Key %d not found\n", k);
            return;
        }

        bool flag = (idx == node->n);

        // 재귀 들어가기 전, 최소 개수 미만일 경우 보충
        if (node->children[idx]->n < T)
            fill(node, idx);

        if (flag && idx > node->n)
            removeFromNode(node->children[idx - 1], k);
        else
            removeFromNode(node->children[idx], k);
    }
}

너무 길고 그림을 그리는 문제를 풀때 해석하기 난해하다. 그러므로 예찬 선생님이 풀어주신 해법으로 다음 포스팅에 정리해보겠다.