BST(Binary Search Tree)

Devkty·2025년 4월 18일
BSTweek 5알고리즘 개념크래프톤 정글 연대기

크래프톤 정글(C언어 WEEK 5 ~ 8)

목록 보기
18/71

사실상 코어타임을 하면서 가상화(도커, 하이퍼 V), malloc 에 대해 개념을 학습했어야 했는데, 못했다. 다음에 다시 알아보는 것으로 하고 시현님이 설명해주신 BST에 대해 재정리를 해보고자 한다.
[참고 사이트]
https://github.com/sihyun10/data_structures_docker/wiki/BST-(Binary_Search_Tree)

BST란?

모든 원소는 유일한 key 값을 갖는다 (중복 없음)

  • 왼쪽 서브 트리의 모든 원소들은 루트(root)의 키보다 작은 값을 갖는다.
  • 오른쪽 서브 트리의 모든 원소들은 루트(root)의 키보다 큰 값을 갖는다.
    즉 왼쪽 서브트리 < 루트 < 오른쪽 서브트리 순서이다.

물론 왼쪽 서브트리, 오른쪽 서브트리 모두 이진 탐색트리이다.

BST의 특징

  • 하나의 루트 노드와 0개 이상의 하위 트리로 구성되어 있습니다.
  • 데이터를 순차적으로 저장하지 않기 때문에 비선형 자료구조입니다.
  • 트리내에 또 다른 트리가 있는 재귀적 자료구조입니다.
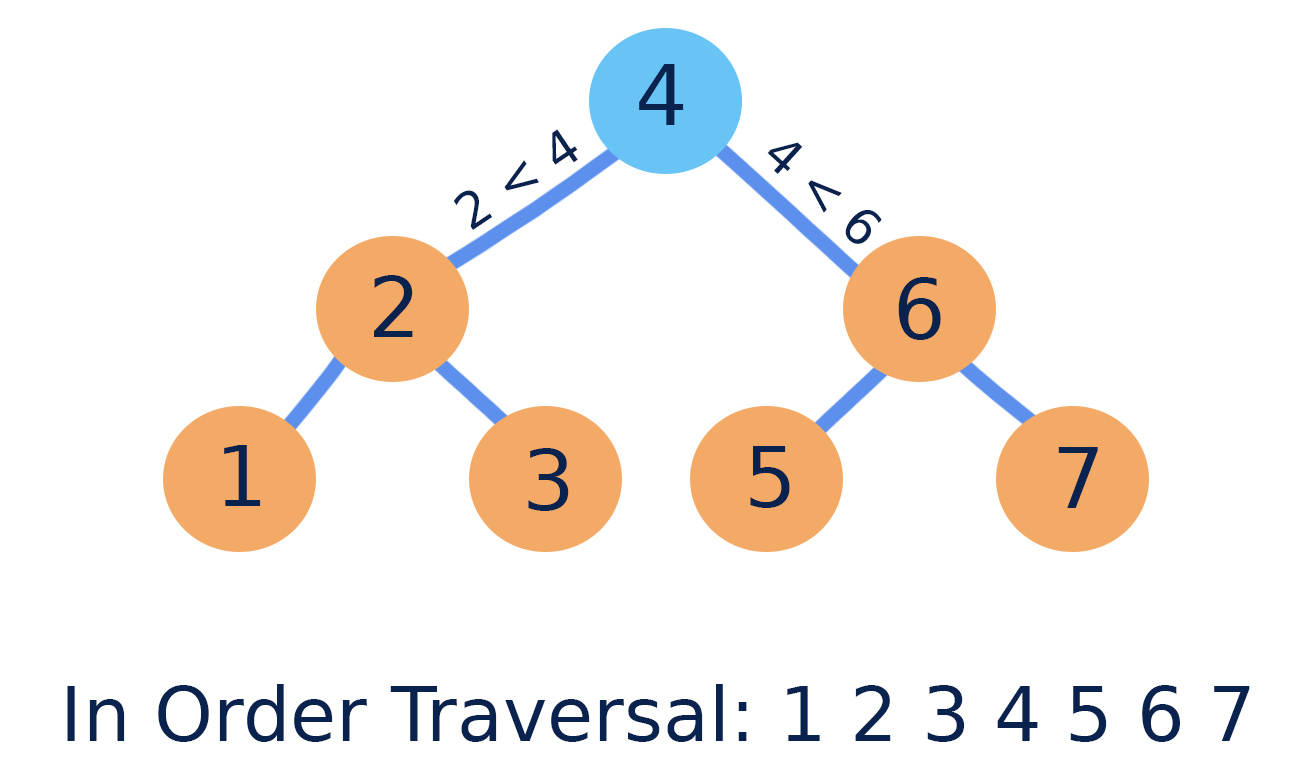
  • 중위 순회(Inorder Traversal)를 수행하면 정렬(오름차순)된 값이 나옵니다.
  • 노드 간에 부모 자식 관계를 갖고 있는 계층형 자료구조이며 모든 자식 노드는 하나의 부모 노드만 갖습니다.

시간복잡도

이진 탐색 트리의 세 개 연산 (검색, 삽입, 삭제) 는 결국 트리를 순회하며 타겟 데이터의 위치를 찾는 연산이 공통적으로 필요하므로, 트리의 균형 상태에 따라 달라집니다.
평균의 경우 logN이 맞지만, 최악의 경우 한쪽으로만 길게 뻗어서 선형 리스트처럼 작동합니다.

→ 균형 상태 : O(logN), 불균형 상태 : 최대 O(N)

그러면 BST를 구조체부터 검색, 삽입, 삭제까지 차근차근 구축해 나가보자.

BST 구조체

구조체는 BST의 특징에 따라 다음과 같이 정의 가능합니다. 각각의 자식 노드를 가르킵니다.

// 이진 탐색 트리 노드 1개를 나타내는 구조
typedef struct BSTnode {
  int item;
  struct BSTnode *left;
  struct BSTnode *right;
} BST_NODE;
  • item: 이 노드가 가지는 정수 데이터
  • left: 왼쪽 자식 노드의 주소
  • right: 오른쪽 자식 노드의 주소

→ 왜 left, right는 자기참조(self-reference) 구조체일까?
이진트리에서 노드가 다른 노드를 가리켜야 하는데, 왜 자기 자신을 가리키는 포인터를 써야하할까?
트리는 노드들끼리 연결되어 계층 구조를 만들어야한다.

// 10은 루트(root) 노드
// 10의 왼쪽 자식 : 5 (root->left = 주소_5)
// 10의 오른쪽 자식 : 15 (root->right = 주소_15)

      10
     /  \
    5   15

노드끼리 서로 주소로 연결되어야 트리 구조를 형성할 수 있다. → 트리 구조는 재귀적인 구조이다.

        10
       /
      5

5만 보면 "루트 노드"가 될 수 있다.

트리는 이렇게 작은 트리들이 계속 연결된 구조이기 때문에, 자식들도 똑같이 BST Node니까 ‘각 노드가 자신의 자식 노드를 가리켜야한다’ 그래서 자기 자신을 참조하는 포인터를 사용해 자식 노드를 연결한다.

즉, left, right는 자식 노드와 연결하는 통로이며 그걸 통해 노드끼리 연결되어 트리 구조가 만들어지는 것이다.

삽입 방법

재귀적으로 알맞은 위치로 찾아가 새 노드를 붙여줍니다. insertBSTNode함수는 다음과 같이 인자를 받습니다.

void insertBSTNode(BSTNode **node, int value)
  • *node: 포인터를 수정하려면 이중 포인터가 필요
  • value: 삽입할 값

위를 활용해서 코드를 작성하면 다음과 같이 작성할 수 있습니다.

//main() 함수 일부분 - 삽입 함수 호출 부분
case 1:
  printf("Input an integer that you want to insert into the Binary Search Tree: ");
  scanf("%d", &i);
  insertBSTNode(&root, i);
  break;

//insertBSTNode() 함수
void insertBSTNode(BSTNode **node, int value){
  if (*node == NULL)
  {
    *node = malloc(sizeof(BSTNode));

    if (*node != NULL) {
      (*node)->item = value;
      (*node)->left = NULL;
      (*node)->right = NULL;
    }
  }
  else
  {
    if (value < (*node)->item)
    {
      insertBSTNode(&((*node)->left), value);
    }
    else if (value > (*node)->item)
    {
      insertBSTNode(&((*node)->right), value);
    }
    else
      return; //중복은 삽입 X
  }
}

[동작 과정]
예시로 10,5,15 삽입합니다.

  1. root == NULL 인 경우, insertBSTNode(&root, 10)
    새로운 노드를 만들어서 root에 연결합니다.
  2. insertBSTNode(&root, 5)
    5 < 10 이므로 "왼쪽"으로 이동 -> Left가 NULL
    left에 새 노드 연결됩니다.
  3. insertBSTNode(&root, 15)
    15 > 10 이므로 "오른쪽"으로 이동 -> Right가 NULL
    right에 새 노드 연결됩니다.
  • value < node->item : 왼쪽 서브트리로 이동 (재귀)
  • value > node->item : 오른쪽 서브트리로 이동 (재귀)

[실습]

→ 그럼 만약 이 상태에서 ‘7’을 추가하면 어떻게 작동할지 직접 해보겠습니다.

insertBSTNode(&root, 7)
    10
   /  \
  5    15

위의 작동 순서에 따라 다음과 같이 작동합니다.

  1. 7 < 10 (root) : 왼쪽(5)로 재귀
  2. 7 > 5 : 오른쪽(NULL)로 재귀
  3. NULL이므로 여기에 새 노드 생성합니다.
    10
   /  \
  5    15
   \
    7

결과는 위와 같습니다.

탐색 방법

[동작 과정]

  1. value == node->item 찾는 값이 현재 노드의 값과 같다면 찾은 것이다.
  2. value < node->item 찾는 값이 작으면 왼쪽 서브트리로 탐색한다.
    2.1 value > node->item 찾는 값이 크면 오른쪽 서브트리로 탐색한다.

위의 로직을 코드로 구현하면 다음과 같습니다.

BSTNode* searchBSTNode(BSTNode* node, int value) {
  if (node == NULL) {
    return NULL; // 트리가 비어있음 or 못 찾음
  }

  if (value == node->item) {
    return node;
  }

  if (value < node->item) {
    return searchBSTNode(node->left, value); // 왼쪽 서브트리 탐색
  } else {
    return searchBSTNode(node->right, value); // 오른쪽 서브트리 탐색
  }
}

[실습]

현재 트리 상태가 아래와 같다고 가정하겠습니다.

        10
       /  \
      5    15
     / \
    3   7

→ 7을 이 트리에서 검색한다면 어떻게 될지 직접 해보겠습니다.

  1. 루트 노드 10에서부터 시작됩니다.
    10(root) > 7 이므로 왼쪽 서브트리(5)로 이동합니다.
  2. 왼쪽 자식 노드 5로 이동
    5(왼쪽 자식 노드) < 7 이므로 오른쪽 자식 노드(7)로 이동합니다.
  3. 오른쪽 자식 노드 7에 도달하면서 값 7 일치함을 알 수 있습니다.

결론적으로 10(root) → 5 → 7 순서로 찾습니다.

삭제 과정

[동작 과정]

삭제 과정은 다른 과정과 달리 좀 복잡합니다. 고려할 사항이 많기 때문입니다. 이전에 배운 B-Tree의 이론을 떠올리면 이해하는데 좀더 편할 것으로 생각됩니다.

노드의 삭제 후에도 트리의 구성을 유지해야하기에 이진 탐색 트리(BST)에서의 삭제 연산은 3가지 경우로 나뉩니다.

  1. 삭제할 노드가 자식이 없는 경우 - 리프노드(Leaf Node)일시
    1-1. 단순히 그 노드를 트리에서 제거. 부모 노드의 해당 자식 포인터를 NULL로 설정합니다.
  2. 삭제할 노드가 하나의 자식만 있는 경우 - 왼쪽 자식만 or 오른쪽 자식만
    2-1. 그 자식 노드를 부모 노드가 가리키게 합니다.
    2-2. 삭제할 노드의 부모가 그 노드의 자식 노드를 가리키게 됩니다.
  3. 삭제할 노드가 두 개의 자식을 가지고 있는 경우
    3-1. 후속 노드(successor) or 선행 노드(predecessor)를 사용해 노드를 삭제합니다.
    → 선행 노드 : 왼쪽 서브트리에서 가장 큰 값(오른쪽)을 가지는 노드
    → 후속 노드 : 삭제할 노드의 오른쪽 서브 트리에서 가장 작은 값(왼쪽)을 가지는 노드

[실습]

1 ~ 2번은 잘 이해가 되지만, 3번은 이해가 잘 안갈 수 있다. 그러므로 예제로 들어서 보겠습니다.

이 트리에서 "노드 5"를 삭제해보겠습니다.

        10
       /  \
      5    15
     / \    / \
    3   7  12  20

먼저, 후속 노드를 찾습니자.

  1. 5를 삭제할 노드는 자식이 2개 있음. 이때 5의 오른쪽 자식(7)이 있습니다.
  2. 7은 왼쪽 서브트리가 없고, 더 이상 작은 값이 없으므로 7이 바로 후속 노드가 됩니다.
  3. 후속 노드인 7을 삭제할 노드인 5의 자리로 이동합니다. (=복사)
// 결과

        10
       /  \
      7    15
     /     / \
    3     12  20

  • 그 후에 후속 노드인 7을 삭제함

    → 왜 7을 삭제하나요?
    5의 자리에 7을 복사합니다. 그러면 트리의 5의 자리에 7이 들어가게 됩니다. 이제 원래 7이 있었던 자리는 필요 없으므로, 그 자리에 있던 7을 삭제합니다. (후속 노드가 트리에서 중복되지 않도록 하기 위함)

[전체 코드]

그럼 전체적인 코드를 살펴보겠습니다.

#include <stdio.h>
#include <stdlib.h>

typedef struct Node {
  int value;
  struct Node* left;
  struct Node* right;
} Node;

Node* createNode(int value) {
  Node* newNode = (Node*)malloc(sizeof(Node));
  newNode->value = value;
  newNode->left = NULL;
  newNode->right = NULL;
  return newNode;
}

//오른쪽 서브트리에서 가장 작은 값 (후속 노드 찾는 함수)
Node* findMin(Node* node) {
  while (node && node->left != NULL) {
    node = node->left;
  }
  return node;
}

Node* deleteNode(Node* root, int value) {
  if (root == NULL) {
    return root;
  }

  if (value < root->value) {
    root->left = deleteNode(root->left, value);
  } else if (value > root->value) {
    root->right = deleteNode(root->right, value);
  } else {
    //삭제할 노드를 찾은 경우다!

    // 1. 삭제할 노드가 자식이 없는 경우
    if (root->left == NULL && root->right == NULL) {
      free(root);
      root = NULL;
    }

    // 2. 삭제할 노드가 하나의 자식만 있는 경우
    else if (root->left == NULL) {
      Node* temp = root;
      root = root->right;
      free(temp);
    } else if (root->right == NULL) {
      Node* temp = root;
      root = root->left;
      free(temp);
    }

    // 3.삭제할 노드가 두 개의 자식을 가지고 있는 경우
    else {
      Node* temp = findMin(root->right);
      root->value = temp->value; //후속 노드 값을 현재 노드에 복사
      root->right = deleteNode(root->right, temp->value);
    }
  }
  return root;
}

main() 코드(예시)

int main() {
  Node* root = createNode(10);
  root->left = createNode(5);
  root->right = createNode(15);
  root->left->left = createNode(3);
  root->left->right = createNode(7);
  root->right->left = createNode(12);
  root->right->right = createNode(20);
       10
      /  \
     5    15
    / \    / \
   3   7  12  20

위와 같은 트리가 만들어집니다.

[실습]

그럼 이제 3가지 경우로 삭제해봅니다.

Case 1. 자식이 없는 경우 

// 1. 삭제할 노드가 자식이 없는 경우
if (root->left == NULL && root->right == NULL) {
  free(root);
  root = NULL;
}
  1. 단순히 노드를 삭제하고 NULL로 설정해주면 됩니다.
root = deleteNode(root, 3);
       10
      /  \
     7    15
         / \
        12  20

12를 삭제했다는 가정 하에 아래 그림과 같습니다.

       10
      /  \
     7   15
           \
           20

Case2. 하나의 자식만 있는 경우

그 자식 노드를 삭제할 노드의 위치로 끌어올리는 방식으로 처리됩니다.

else if (root->left == NULL) {
  Node* temp = root;
  root = root->right;
  free(temp);
} 
else if (root->right == NULL) {
  Node* temp = root;
  root = root->left;
  free(temp);
}
root = deleteNode(root, 15);

현재 경우는 root → left == NULL 인 경우이다.

  • 현재 삭제하려는 노드(root)를 임시 포인터 temp에 저장합니다. → 왜 저장하나? root를 다른 노드로 바꿀꺼라서 기존 노드를 free()로 삭제하려면 잠깐 저장합니다.
  • root = root->right; (현재 노드인 root삭제하고, 그 자리에 오른쪽 자식이 대신 오게끔) → root->20를 가리키게 됩니다.
  • free(temp); 아까 임시로 저장해뒀던 삭제할 노드를 메모리에서 해제(제거) → 15를 메모리에서 해제
//최종 결과

       10
      /  \
     7   20

Case 3. 자식이 두 개인 경우

Node* findMin(Node* node) {
  while (node && node->left != NULL) {
    node = node->left;
  }
  return node;
}

    // 3.삭제할 노드가 두 개의 자식을 가지고 있는 경우
    else {
      Node* temp = findMin(root->right);
      root->value = temp->value; //후속 노드 값을 현재 노드에 복사
      root->right = deleteNode(root->right, tmep->value); //후속 노드 있었던 위치에서 해당 값 다시 재귀적으로 삭제
}
  root = deleteNode(root, 5); //5를 삭제
  1. 오른쪽 서브트리에서 가장 작은 값(후속노드 = 7)을 찾습니다.
  2. 그 값을 현재 노드의 값으로 대체하고, 후속 노드 삭제합니다.
       10
      /  \
     7    15
    /     / \
   3     12  20
profile
Devkty
모든걸 기록하며 성장하고 싶은 개발자입니다. 현재 크래프톤 정글 8기를 수료하고 구직활동 중입니다.
이전 포스트

WEEK5 퀴즈 복습

다음 포스트

이동석 코치님 C언어 강연

0개의 댓글