5주차 퀴즈 복습
시간이 좀 됐지만, 5주차의 마무리를 해야하므로 퀴즈 내용을 복습해봤다. B-Tree를 설명할 정도로 능숙했지만, 문제를 잘 못 읽어 1, 2번 문제 틀린게 아직까지 마음이 아프다…
1번 문제
차수가 3인 아래 B-Tree에서 17을 새로 삽입한 후의 결과를 그려보세요.
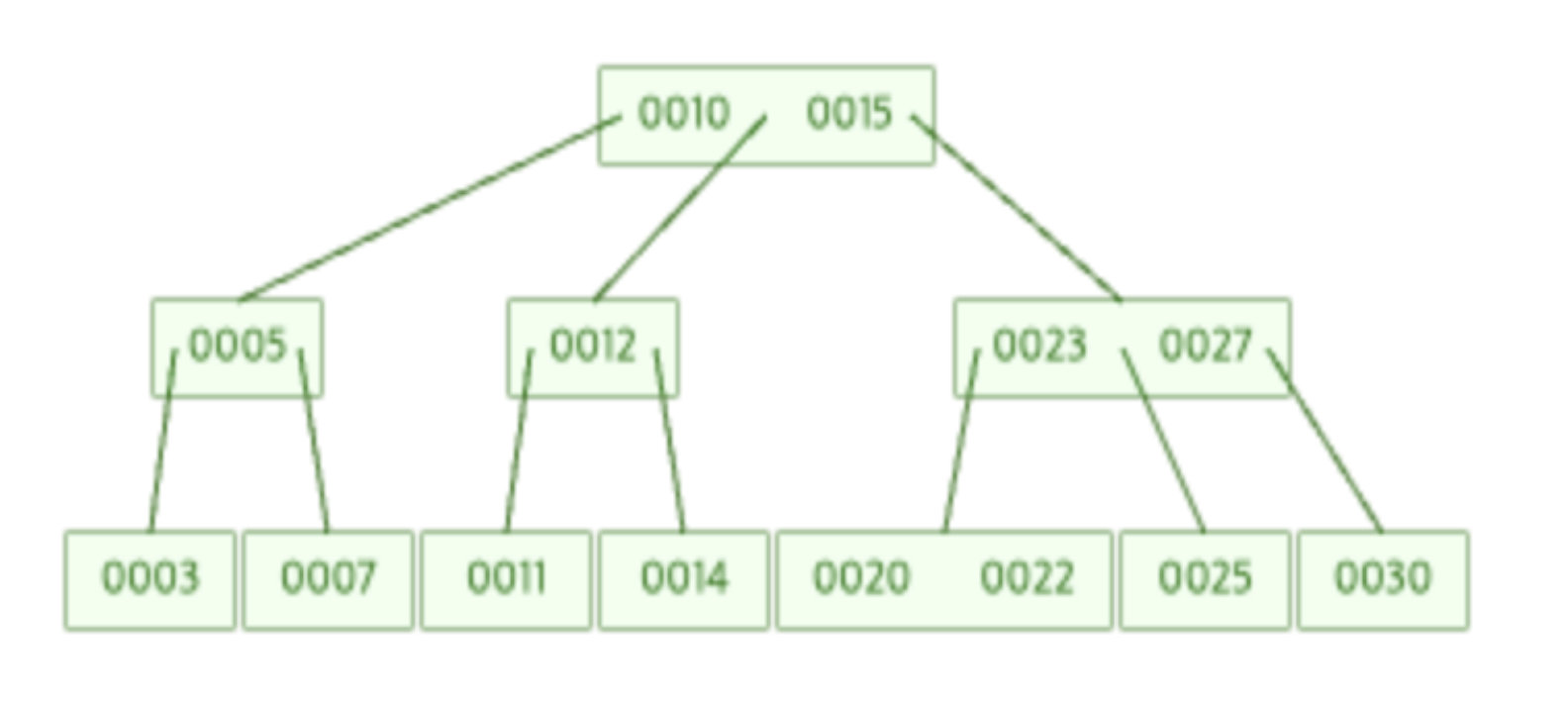
→ 이것은 내가 전에 설명한 B-Tree 삽입 로직을 생각하여 풀면된다. 17이 들어가면 15보다 크고, 23보다 작으므로 [20, 22] 자식 노드에 포함되게 된다. 그러나 해당 트리는 차수가 3이므로 자식이 최대 2개이다.
그러므로 [17, 20, 22]에서 중간 인자인 20은 승급한다. 승급된 이후 부모노드가 [20, 23, 27]이므로 부모노드에서도 23이 승급합니다. 그러면 그 위의 부모노드도 [10, 15, 23]에서 15가 승급하게 된다.
완성되면 밑에 트리와 같이 그려진다.
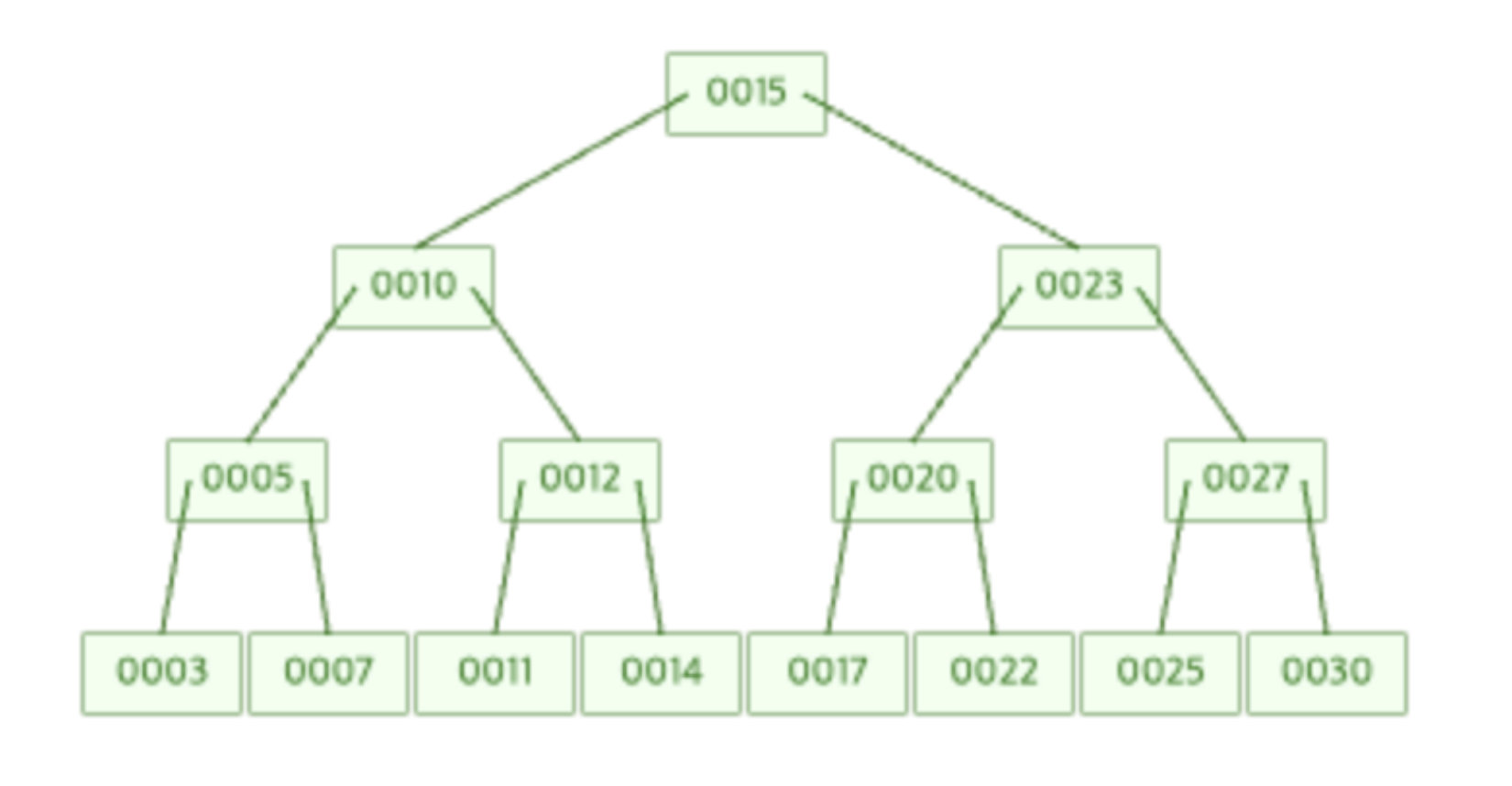
2번 문제
1번의 결과에서 20을 삭제한 후의 B-Tree의 모습을 그려 보세요. Leaf-Node가 아닌 노드를 삭제할 경우에는 전임자(Predecessor)와 위치를 바꾼 후 삭제를 진행합니다.
→ 위의 트리에서 20을 삭제한다면, 부모에게 23을 받아 오고 형제 노드 27과 합칩니다. 그러면 원래의 부모 노드의 값이 사라지므로 그 부모노드의 위의 부모노드 15를 불러 옵니다. 그러고 형제 노드 10과 합칩니다. 과정을 완료하면 밑에 트리와 같게 나옵니다.
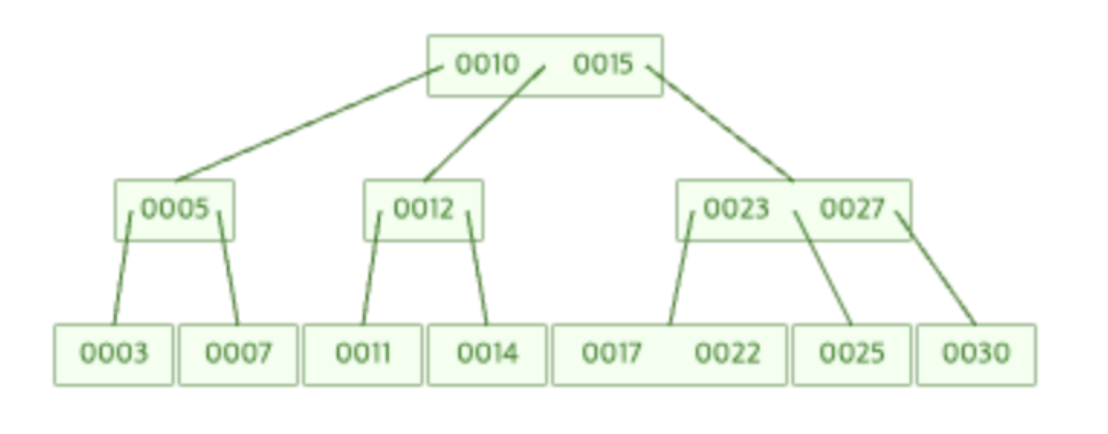
3번 문제
다음 C 코드의 문제점을 찾아 해결하고, printf 출력 결과를 적으시오.
#include <stdio.h>
#include <stdlib.h>
int main() {
int *arr = (int *)malloc(5 * sizeof(int));
for (int i = 0; i < 5; i++) {
arr[i] = i * i;
}
printf("%d\n", arr[3]); // 결과 기입
// start of code
….
// end of code
return 0;
}→ 3-1 문제점 해결
free(arr); 를 return 0;위에 추가하여 메모리 누수를 없앱니다. malloc이 동적 메모리 할당을 하기 때문입니다.
→ 3-2 실행결과
3 * 3 이므로 9가 답입니다.
4번 문제
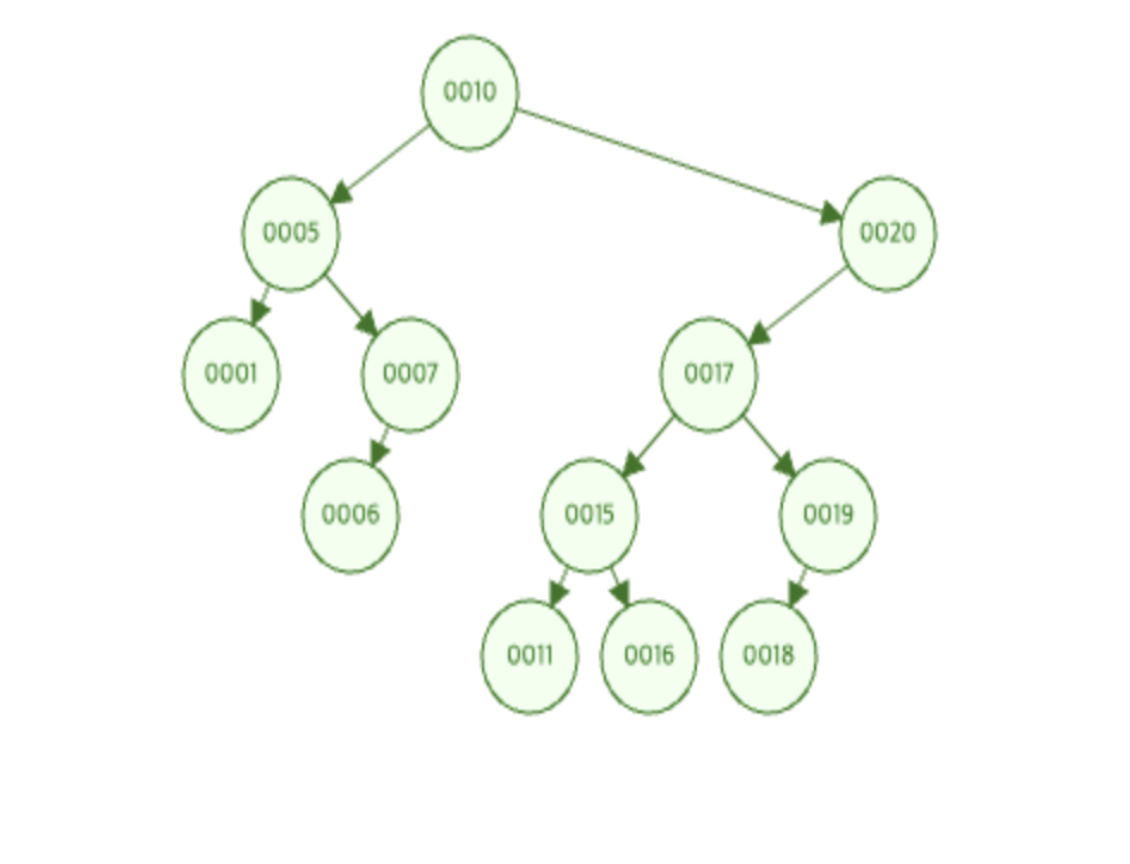
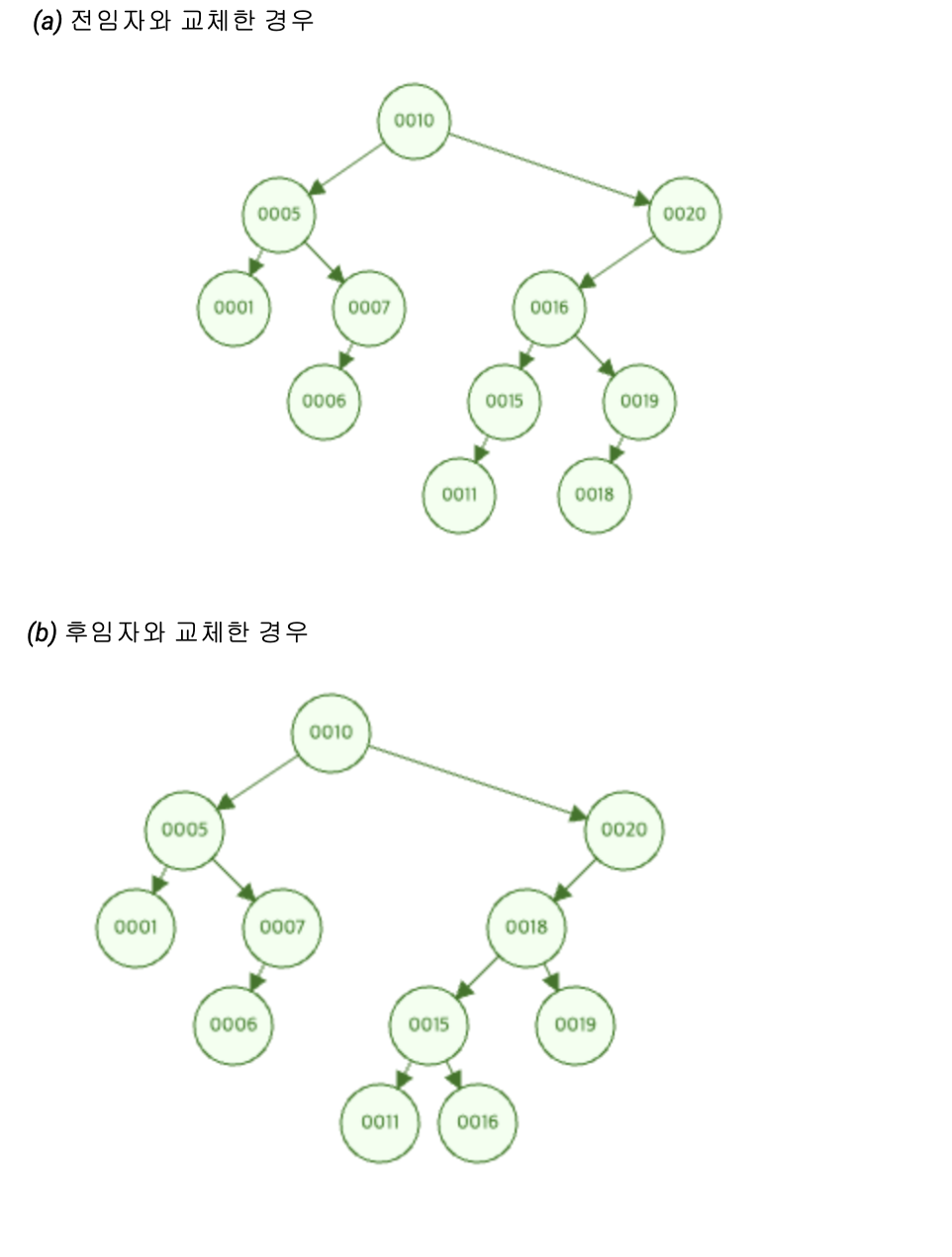
아래와 같은 이진 탐색 트리가 있다고 할 때, 트리의 노드 17을 삭제한 다음의 결과를 그려보세요. 리프 노드가 아닌 노드를 삭제할 때 해당 노드를 전임자(Predecessor)와 후임자(Successor)로 대체할 때의 결과를 각각 그리세요.
1590159-451d-4b70-83ef-d09975fb385b:스크린샷_2025-04-18_02.55.25.png)
→ 해당 문제는 굉장히 쉽습니다. 전임자(대상 기준 왼쪽 자식트리의 맨 오른쪽 노드)와 후임자(대상 기준 오른쪽 자식트리의 맨 왼쪽 노드)의 개념만 잘 알고 있으면 됩니다. 모르면 B-Tree 포스팅을 참고해주세요.
그래서 다음과 같이 나타납니다.
5번 문제
다음 코드를 실행했을 때 printf 출력 값이 2 3 4 5 6 이 되도록 func 함수를 완성하시오.
#include <stdio.h>
void func(/*....*/) {
// ....
}
int main() {
int arr[5] = {1, 2, 3, 4, 5};
func(arr, 5);
for (int i = 0; i < 5; i++)
printf("%d ", arr[i]);
return 0;
}→ func 함수는 i를 1씩 올려주면서 포인터를 통해 다음 리스트로 옮겨질 수 있어야합니다. 그러므로 다음과 같이 나타낼 수 있습니다.
void func(int *p, int n) {
for (int i = 0; i < n; i++) // i값 도 n전까지 +1
{
*p = *p + 1; // 리스트 다음값 입력을 위해 포인터 값은 +1
p++; // 다음 인자를 넣기 위해 +1
}
}6번 문제
피보나치 수열(1, 1, 2, 3, 5, 8, ….)의 n번째 항의 값을 리턴하는 함수를 파이썬을 사용해 dynamic programming의 상향식 접근법, 하향식 접근법으로 작성하시오. (python 문법이 정확할 필요는 없음)
→ 다음과 같이 나타낼 수 있습니다.
# (1) 상향식 접근법
def fib_bottom_up(n):
# n이 1일 경우 바로 값을 반환
if n <= 1:
return n
# 초기 두 피보나치 수
fib_0 = 0
fib_1 = 1
# 피보나치 수를 계산
for i in range(2, n + 1):
# 다음 피보나치 수는 이전 두 수의 합
next_fib = fib_0 + fib_1
# 이동
fib_0 = fib_1
fib_1 = next_fib
return fib_1
# (2) 하향식 접근법
def fib_top_down(n, memo=None):
# 메모이제이션을 위한 리스트 초기화
if memo is None:
memo = [-1] * (n + 1)
# 기저 조건
if n <= 1:
return n
# 이미 계산된 값이면 반환
if memo[n] != -1:
return memo[n]
# 재귀적으로 피보나치 수 계산
memo[n] = fib_top_down(n - 1, memo) + fib_top_down(n - 2, memo)
return memo[n]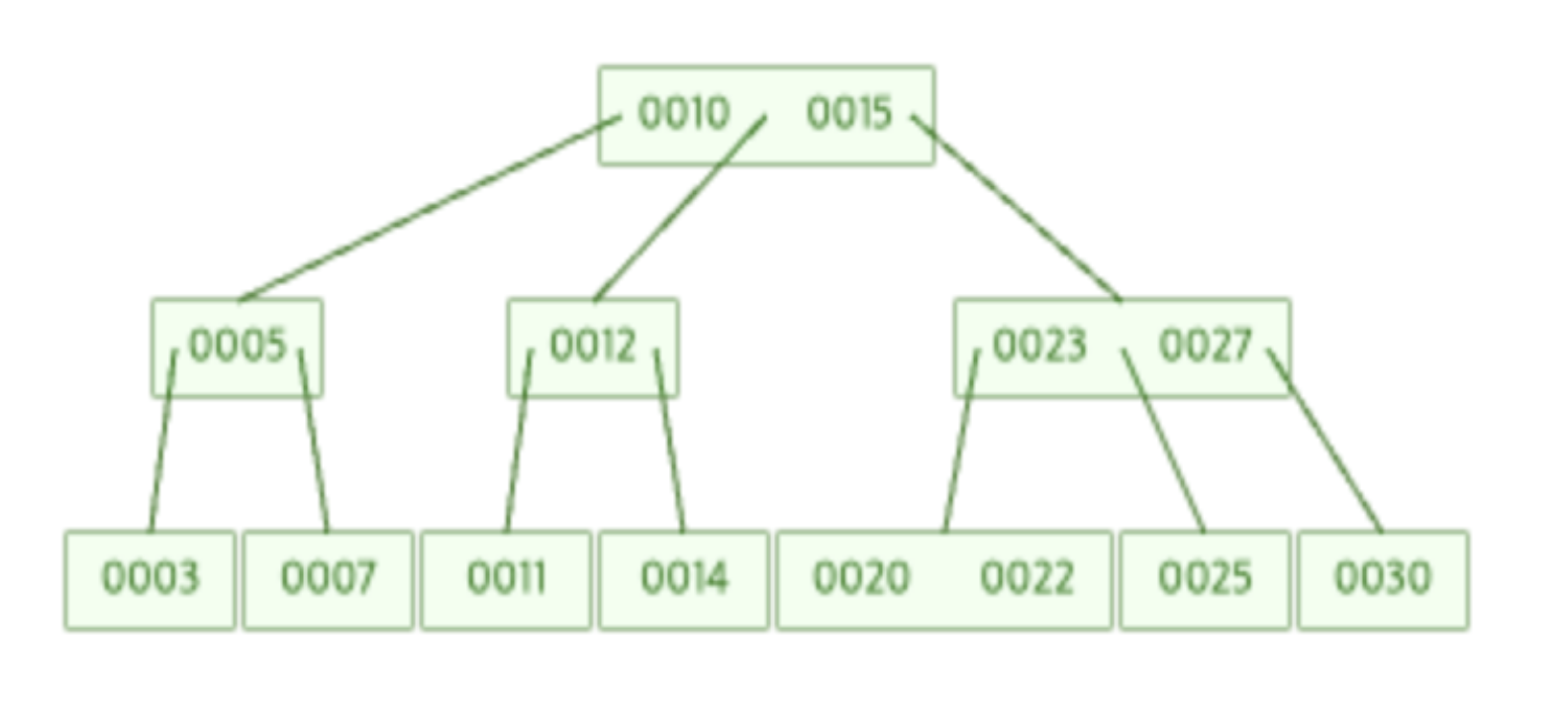

B트리의 모든 리프노드 레벨이 같은 이유가 무엇이라 생각하십니까?